- Fonction de Dirichlet
-
Dirichlet (homonymie)
Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.Johann Peter Gustav Lejeune Dirichlet est un mathématicien allemand du XIXe siècle dont le travail est surtout en théorie des nombres.
Arithmétique
Plusieurs théorèmes portent son nom :
- Le théorème de Dirichlet détermine que pour tous entiers naturels non nuls a et b premiers entre eux, il existe une infinité de nombres premiers congrus à a modulo b.
- Le théorème des unités de Dirichlet détermine le rang du groupe d'unités dans l'anneau.
Fonctions
Des fonctions mathématiques portent son nom :
- Un caractère de Dirichlet est une fonction
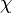de l'ensemble des nombres entiers dans l'ensemble des nombres complexes. - Le noyau de Dirichlet est un polynôme trigonométrique qui intervient notamment dans l'étude de la convergence des séries de Fourier.
- Le produit de convolution de Dirichlet ou le produit de Dirichlet est une loi de composition définie sur l’ensemble des fonctions arithmétiques.
- On appelle aussi fonction de Dirichlet la fonction caractéristique de
. C'est une fonction partout discontinue, donnée comme exemple de fonction non intégrable (à l'époque)[1].
Plus particulièrement, certaines concernent la fonction zêta de Riemann :
- La série de Dirichlet est la forme générale de la fonction zêta de Riemann.
- La fonction β de Dirichlet est un des exemples les plus simples de fonction zêta de Riemann.
- La fonction êta de Dirichlet est définie à partir de la fonction zêta de Riemann.
Références
- ↑ L. Dirichlet, Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données, paru dans le Journal de Crelle, J. Reine Angew. Math 4 (1829) 157-169, reproduit dans Jean-Pierre Kahane, Pierres Gilles Lemarié-Rieusset, Séries de Fourier et ondelettes, Cassini (1998), 48-60).
Catégorie : Homonymie
Wikimedia Foundation. 2010.
