Processus de gauss

Processus de gauss

Processus de Gauss

Cette notion se rencontre dans des domaines variés allant des vibrations mécaniques aux vagues de la mer. De même que le théorème de la limite centrale permet de considérer une somme de variables aléatoires indépendantes comme une variable de Gauss, il conduit également à considérer une somme de processus aléatoires indépendants comme un processus de Gauss.

Dans un cas comme dans l'autre, une transformation linéaire conserve ce caractère gaussien car un filtre linéaire qui conserve la fréquence d'un signal sinusoïdal, conserve également les fréquences d'un processus gaussien. Ceci permet d'utiliser des méthodes analogues dans les deux cas (voir par exemple Linéarisation équivalente).

Sommaire

Propriété fondamentale

À un signal à variance finie est associée une fonction d'autocovariance (voir Analyse spectrale). Dans les problèmes pratiques on n'a accès qu'à un enregistrement de durée limitée, ce qui constitue une perte d'information. La transformation de Fourier permet d'obtenir la densité spectrale, c'est-à-dire le contenu en fréquences du signal. En considérant le signal comme une réalisation d'un processus stationnaire ergodique, cette dernière caractéristique supposant que sa moyenne a été soustraite, l'autocovariance statistique de ce processus est égale à l'autocovariance temporelle. Elle permet de déterminer les matrices d'autocovariance pour des décalages temporels variés. Si le processus est gaussien, ces matrices suffisent pour le décrire à tous ordres. Ainsi l'autocovariance décrit entièrement le processus.

Représentation de Rice

La représentation d'un processus gaussien centré sous la forme

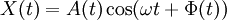
X(t) = A(t) \cos(\omega t + \Phi(t))\,

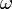\omega\, : constante

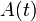A(t)\, : processus aléatoire à valeurs positives ou nulles

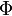\Phi\, : processus aléatoire sur un intervalle ]0,2\pi]\,

permet d'obtenir des résultats intéressants. Pour cela il faut également considérer le processus

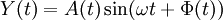
Y(t) = A(t) \sin(\omega t + \Phi(t))\,

Les deux processus gaussiens ont même variance 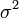\sigma^2\, et sont décorrélés donc indépendants. Leur densité de probabilité jointe se réduit donc à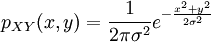

p_{XY}(x,y) = \frac {1} {2\pi \sigma^2} e^{-\frac {x^2 + y^2} {2 \sigma^2}}

Le changement de variables défini par les deux formules du début conduit à une densité de probabilité jointe qui montre que les deux nouveaux processus sont indépendants :

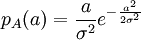p_A(a) = {a \over\sigma^2} e^{-{a^2 \over {2 \sigma^2}}}\, : processus de Rayleigh


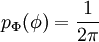p_\Phi(\phi) = {1 \over {2\pi}}\, : processus uniforme

Interprétation

Processus de Gauss.png

Le processus gaussien est donc décrit par un processus vaguement sinusoïdal 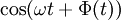\cos(\omega t + \Phi(t))\, modulé par un processus enveloppe A(t)\,.

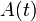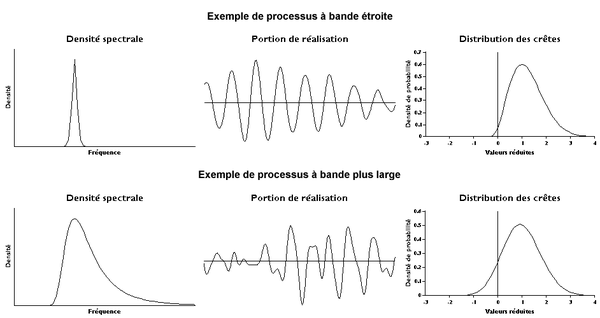
Un processus à bande étroite, somme de sinusoïdes de fréquences voisines, apparaît comme une sinusoïde modulée. La densité de probabilité de l'enveloppe représente alors approximativement la densité de probabilité des crêtes. La même loi s'applique aux amplitudes crête-creux avec une moyenne quadratique doublée.

Dans le cas d'un processus à large bande, ce résultat n'est plus valable car les hautes fréquences superposées à des creux basses fréquence font apparaître des crêtes négatives. Un raisonnement nettement plus compliqué conduit à la loi dite de Huston-Skopinski, parfois aussi appelée loi de Rice :

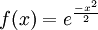
f(x) = e^{-x^2 \over 2}
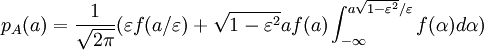
p_A(a) = {1\over \sqrt{2 \pi}} (\varepsilon f(a/\varepsilon) + \sqrt{1 - \varepsilon^2} a f(a) \int_{-\infty}^{a \sqrt{1 - \varepsilon^2} / \varepsilon} f(\alpha) d\alpha)

\varepsilon : paramètre compris entre 0 et 1 associé à la largeur du spectre.

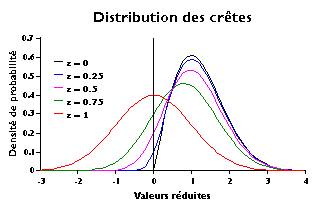
Distribution des crêtes.png

Les deux limites ne peuvent être atteintes. La valeur 0 correspondrait à un spectre ne contenant qu'une fréquence, ce qui ne peut conduire à un phénomène gaussien. La valeur 1 correspond en particulier au bruit blanc parfaitement décorrélé, muni de la même densité spectrale à toutes les fréquences donc de variance infinie. Dans le cas gaussien cette décorrélation assure l'indépendance des variables aléatoires successives, les crêtes ayant alors la même distribution que les valeurs.

Périodes moyennes

Dans les mêmes conditions, il est possible de calculer l'espérance de certaines périodes identique à leur moyenne temporelle, en particulier les moyennes des distances entre deux passages au zéro successifs à pente de même signe et entre deux crêtes successives. La première de ces périodes est utilisée en conjonction avec la loi de Rayleigh pour calculer les dommages en fatigue, si la distribution des contraintes est raisonnablement gaussienne/rayleighienne.

Références

  • (en) (en) Y. K. Lin, Probabilistic Theory of Structural Dynamics, Robert E. Krieger Publishing Company, New York, juillet 1976, 368 p. (ISBN 0882753770) 


Articles de mathématiques en rapport avec les probabilités ou les statistiques
  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques
Ce document provient de « Processus de Gauss ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Processus de gauss de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Processus de Gauss — Cette notion se rencontre dans des domaines variés allant des vibrations mécaniques aux vagues de la mer. De même que le théorème de la limite centrale permet de considérer une somme de variables aléatoires indépendantes comme une variable de… …   Wikipédia en Français

  • Processus aléatoire — Processus stochastique Pour les articles homonymes, voir Processus. Le calcul des probabilités classique concerne des épreuves où chaque résultat possible (ou réalisation) est un nombre, ce qui conduit à la notion de variable aléatoire. Un… …   Wikipédia en Français

  • Processus stochastiques — Processus stochastique Pour les articles homonymes, voir Processus. Le calcul des probabilités classique concerne des épreuves où chaque résultat possible (ou réalisation) est un nombre, ce qui conduit à la notion de variable aléatoire. Un… …   Wikipédia en Français

  • Processus stochastique — Pour les articles homonymes, voir Processus. Le calcul classique des probabilités concerne des épreuves où chaque résultat possible (ou réalisation) est mesuré par un nombre, ce qui conduit à la notion de variable aléatoire. Un processus… …   Wikipédia en Français

  • Processus stationnaire — Pour accéder aux propriétés essentielles d un signal physique il peut être commode de le considérer comme une réalisation d un processus aléatoire (voir quelques précisions dans Processus continu). Le problème est largement simplifié si le… …   Wikipédia en Français

  • Gauss (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Carl Friedrich Gauss (1777 1855), mathématicien, astronome et physicien allemand. Le gauss, une unité de mesure du champ magnétique, noté G. GAUSS, un… …   Wikipédia en Français

  • Processus continu — Pour les articles homonymes, voir Processus. La notion de processus continu correspond à un type de processus stochastique utilisé dans la description des signaux physiques, fonctions généralement régulières du temps. Le présent article aborde en …   Wikipédia en Français

  • STOCHASTIQUES (PROCESSUS) — Le calcul des probabilités classique [cf. PROBABILITÉS (CALCUL DES)] s’applique à des épreuves où chaque résultat possible (ou éventualité) est un nombre . Or il existe beaucoup de situations réelles relevant de modèles aléatoires, mais d’une… …   Encyclopédie Universelle

  • Carl Friedrich Gauss — « Gauss » redirige ici. Pour les autres significations, voir Gauss (homonymie). Carl Friedrich Gauß Portrait de Johann Carl Friedrich Gauss (1777 1855), réalisé par Christian …   Wikipédia en Français

  • Équation de Maxwell-Gauss — Équations de Maxwell  Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”