Probabilité stationnaire d'une chaîne de Markov

La probabilité stationnaire $\scriptstyle\ \pi=(\pi_i)_{i\in E}\quad$ d'une chaîne de Markov $\scriptstyle\ X=(X_n)_{n\ge 0}\quad$ s'interprète usuellement comme la fraction du temps passé en chaque état $\scriptstyle\ i\$ de l'espace d'états $\scriptstyle\ E\$ de cette chaîne de Markov, asymptotiquement. En effet, une version de la loi forte des grands nombres pour les chaînes de Markov stipule que :

$\pi_i\ =\ \lim_n\ \frac{1_{X_0=i}+1_{X_1=i}+\dots+1_{X_{n-2}=i}+1_{X_{n-1}=i}}{n}\ =\ \lim_n\ \frac{S_n(i)}{n},$

presque sûrement, sous certaines hypothèses détaillées plus bas. La variable aléatoire $\scriptstyle\ S_n(i)\$ s'interprète comme le temps passé en $\scriptstyle\ i\$ lors des $\scriptstyle\ n\$ premiers pas de la chaîne de Markov $\scriptstyle\ X.$ La fraction $\scriptstyle\ S_n(i)/n\$ est donc la fraction de temps passé en l'état $\scriptstyle\ i\$ pendant les $\scriptstyle\ n\$ premiers pas de la chaîne de Markov. La convergence de cette fraction lorsque $\scriptstyle\ n\$ tend vers l'infini n'est pas un résultat anodin. On trouvera une discussion plus poussée sur le temps de séjour sur la page Récurrence et transience d'une chaîne de Markov.

Définition

Définition —

Une mesure $\scriptstyle\ \mu=(\mu_i)_{i\in E}\quad$ sur l'espace d'états $\scriptstyle\ E\$ d'une chaîne de Markov $\scriptstyle\ X=(X_n)_{n\ge 0}\quad$ de matrice de transition $\scriptstyle\ P=\left(p_{i,j}\right)_{(i,j)\in E^2}\quad$ est dite stationnaire si

$\mu = \mu\,P,$

ou, de manière équivalente,

$\forall j\in E,\qquad \mu_j = \sum_{i\in E}\mu_i\,p_{i,j}.$

Une mesure stationnaire est une fonction propre de la transposée de la matrice de transition, associée à la valeur propre 1.

Une mesure stationnaire $\scriptstyle\ \pi\quad$ est appelée probabilité stationnaire ou loi stationnaire si elle remplit les conditions supplémentaires :

$\forall i\in E, \qquad \pi_i\ \ge\ 0,$

$\text{et}\qquad\sum_{i\in E}\pi_i\ =\ 1.$

Remarques :

La chaîne de Markov $\scriptstyle\ X=(X_n)_{n\ge 0}\quad$ est un processus stationnaire, i.e., pour tout $\scriptstyle\ n\ge 1,\quad$ $\scriptstyle\ \left(X_n, X_{n+1}, X_{n+2}, \dots\right)\quad$ a même loi de probabilité que $\scriptstyle\ \left(X_0, X_{1}, X_{2}, \dots\right),\quad$ si et seulement si la loi initiale de $\scriptstyle\ X\quad$ (la loi de $\scriptstyle\ X_0$ ) est une probabilité stationnaire.
Cela entraîne en particulier que si la loi initiale de la chaîne de Markov $\scriptstyle\ X\quad$ est une probabilité stationnaire, alors la loi de $\scriptstyle\ X_n\$ est cette même probabilité stationnaire, indépendamment de $\scriptstyle\ n.\$
L'ensemble des probabilités stationnaires est convexe.

Existence et unicité : cas irréductible

L'existence d'une probabilité stationnaire $\scriptstyle\ \pi\$ pour une chaîne de Markov irréductible est liée aux propriétés du temps de retour en $\scriptstyle\ i,\$ et en particulier aux propriétés de récurrence de l'état $\scriptstyle\ i.$

Définition —

Le temps de premier retour en $\scriptstyle\ i,\quad$ noté $\scriptstyle\ T_i,\quad$ est une variable aléatoire à valeurs dans $\scriptstyle\ \overline{\mathbb{N}}=\mathbb{N}\cup\{+\infty\},\$ définie par

$T_i=\left\{\begin{array}{ll}\inf\{k\ge 1\,|\,X_k=i\}&\text{ si }\{k\ge 1\,|\,X_k=i\}\neq\emptyset,\\+\infty&\text{ sinon.}\end{array}\right..$

L'état $\scriptstyle\ i\quad$ est récurrent positif si l'espérance du temps de premier retour en cet état, partant de cet état, est finie, i.e. si

$\mathbb{E}_i\left[T_i\right]\ <\ +\infty.$

Rappelons que lorsqu'on étudie une chaîne de Markov particulière, sa matrice de transition est en général bien définie et fixée tout au long de l'étude, mais la loi initiale peut changer lors de l'étude et les notations doivent refléter la loi initiale considérée sur le moment : si à un moment de l'étude on considère une chaîne de Markov de loi initiale définie par $\scriptstyle\ \forall i\in E,\quad \mathbb{P}\left(X_{0}=i\right)=\mu_i,\quad$ alors les probabilités sont notées $\scriptstyle\ \mathbb{P}_{\mu}\left(\dots\right),\quad$ et les espérances sont notées $\scriptstyle\ \mathbb{E}_{\mu}\left[\dots\right].\quad$ En particulier, si $\scriptstyle\ \mathbb{P}\left(X_{0}=j\right)=1,\quad$ on dit que la chaîne de Markov part de $\scriptstyle\ j,\quad$ les probabilités sont notées $\scriptstyle\ \mathbb{P}_{j}\left(\dots\right),\quad$ et les espérances sont notées $\scriptstyle\ \mathbb{E}_{j}\left[\dots\right].\quad$ Ci-dessus, dans la notation $\scriptstyle\ \mathbb{E}_i,\quad$ l'indice $\scriptstyle\ i\quad$ signifie qu'on calcule l'espérance pour la chaîne de Markov partant de $\scriptstyle\ i,\quad$ i.e. de loi initiale définie par $\scriptstyle\ \mathbb{P}(X_0=i)=1.$ Ainsi $\scriptstyle\ \mathbb{E}_i\left[T_i\right]\$ s'interprète comme l'intervalle de temps "typique" entre deux passages consécutifs à l'état $\scriptstyle\ i.\quad$

Théorème — Si une chaîne de Markov est irréductible, alors il existe au plus une probabilité stationnaire. On a alors équivalence entre les 3 propositions :

il existe une probabilité stationnaire,
il existe un état récurrent positif,
tous les états sont récurrents positifs.

Supposons qu'une des 3 conditions ci-dessus est remplie et notons $\scriptstyle\ \pi\quad$ l'unique probabilité stationnaire : alors

$\forall i\in E,\quad \pi_i\ =\ \frac1{\mathbb{E}_i\left[T_i\right]}.$

Théorème — Une chaîne de Markov irréductible à espace d'états fini est récurrente positive (i.e. tous ses états sont récurrents positifs). Elle possède donc exactement une probabilité stationnaire.

La relation entre existence et unicité des probabilités stationnaires, classifications des états de la chaîne de Markov et récurrence positive est traité dans un cadre complètement général à la section Existence et unicité. Cependant les théorèmes ci-dessus, valables uniquement pour les chaînes de Markov irréductibles, sont suffisants dans un grand nombre d'exemples.

Loi forte des grands nombres

Graphe de la marche réfléchie en 0

Distribution empirique (rouge) et distribution stationnaire (bleue) pour la marche réfléchie en 0, départ à la moyenne stationnaire -1+1/ρ=2 : p=0.4, q=0.6, ρ=1/3, 2 000 pas

Distribution empirique (rouge) : départ à la moyenne stationnaire -1+1/ρ=12, p=0.48, q=0.52, ρ=1/13, 2 000 pas

Distribution empirique (rouge) : départ à la moyenne stationnaire -1+1/ρ=12, p=0.48, q=0.52, ρ=1/13, 5 000 pas

Distribution empirique (rouge) : départ à la moyenne stationnaire -1+1/ρ=12, p=0.48, q=0.52, ρ=1/13, 20 000 pas

Dans le cas d'une chaîne de Markov irréductible et récurrente positive, la loi forte des grands nombres est en vigueur : la moyenne d'une fonction $\scriptstyle\ f\$ sur les instances de la chaîne de Markov est égale à sa moyenne selon sa probabilité stationnaire. Plus précisément, sous l'hypothèse

$\sum_{i\in E} |f(i)|\,\pi_i\ < +\infty,$

on a presque sûrement :

$\lim_{n}\; \frac{1}{n} \; \sum_{k=0}^{n-1} f(X_k) \ =\ \sum_{i\in E} f(i)\,\pi_i\ =\ \pi f.$

La moyenne de la valeur des instances est donc, sur le long terme, égale à l'espérance de la probabilité stationnaire. En particulier, cette équivalence sur les moyennes s'applique si $\scriptstyle\ f\$ est la fonction indicatrice d'un sous-ensemble $\scriptstyle\ A\$ de l'espace des états :

$\lim_{n}\; \frac{1}{n} \; \sum_{k=0}^{n-1} 1_A(X_k)\ =\ \sum_{i\in A}\ \pi_i\ =\ \pi(A).$

Cela permet d'approcher la probabilité stationnaire par un histogramme (la distribution empirique) construit à partir d'une séquence particulière.

Ergodicité

En particulier, si le processus est construit en prenant la probabilité stationnaire comme loi initiale, le shift $\scriptstyle\ \theta\$ défini par

$\scriptstyle\ x=(x_0,x_1,x_2,\dots)\in E^{\mathbb{N}}\quad\rightarrow\quad \theta\,x=(x_1,x_2,x_3,\dots)$

préserve la mesure, ce qui fait de la chaîne de Markov un système dynamique. La loi forte des grands nombres entraine alors que la chaîne de Markov est un système dynamique ergodique. L'ergodicité est à la fois plus forte que la loi forte des grands nombres car on peut en déduire, par exemple, que $\scriptstyle\ \frac{1}{n} \; \sum_{k=0}^{n-1} f(X_k,X_{k+1}),\$ a pour limite presque sûre $\scriptstyle\ \sum_{i,j\in E} f(i,j)\,\pi_ip_{i,j},\$ mais elle est aussi plus faible car elle réclame en principe la stationnarité de la chaîne de Markov, ce qui n'est pas le cas de la loi forte des grands nombres.

Convergence vers la loi stationnaire

Convergence de la loi marginale

Si la chaîne de Markov est irréductible, récurrente positive et apériodique, alors $\scriptstyle\ P^k\$ converge vers une matrice dont chaque ligne est l'unique distribution stationnaire $\scriptstyle\ \pi.\$ En particulier, la loi $\scriptstyle\ \mu_n\$ de $\scriptstyle\ X_n\$ converge vers $\scriptstyle\ \pi\$ indépendamment de la loi initiale $\scriptstyle\ \mu_0.\$ Dans le cas d'un espace d'état fini, cela se prouve par le théorème de Perron-Frobenius.

Typiquement, par exemple dans le cas d'une chaîne de Markov à espace d'états fini irréductible, récurrente positive et apériodique, la convergence est exponentiellement rapide, i.e. pour une norme quelconque, on peut trouver $\scriptstyle\ K>0\$ et $\scriptstyle\ \alpha\in]0,1[\$ tels que

$\Vert\mu_n-\pi\Vert \le K\ \alpha^n.$

On trouve plus loin dans l'article une démonstration de cette décroissance exponentielle dans le cas particulier des chaînes réversibles.

Convergence de la mesure empirique

Si la chaîne de Markov est irréductible et récurrente positive alors, par suite de la loi forte des grands nombres, la mesure empirique de la chaîne de Markov,

$\tfrac1n\quad\sum_{k=0}^{n-1}\,\delta_{X_k}\quad=\quad \tfrac1n\quad\sum_{i\in E}\ S_n(i)\,\delta_{i},$

converge vers l'unique distribution stationnaire. Typiquement, par exemple dans le cas d'une chaîne de Markov à espace d'états fini irréductible et récurrente positive, la convergence est, en un certain sens, en $\scriptstyle\ \mathcal{O}(1/\sqrt{n}).$ Cela permet d'approcher la probabilité stationnaire par un histogramme construit à partir d'une séquence particulière. 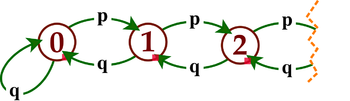Nota: alors que la loi de $\scriptstyle\ X_n,\quad$ notée $\scriptstyle\ \mu_n\quad$ ci-dessus, est une mesure de probabilité fixée, la loi empirique est, elle, une mesure de probabilité aléatoire, ou bien, si l'on veut, une variable aléatoire à valeurs dans les mesures de probabilité.

Marche aléatoire réfléchie :

C'est la chaîne de Markov d'espace d'états $\scriptstyle\ E=\mathbb{N},\quad$ de matrice de transition définie par $\scriptstyle\ p_{k,k+1}=p,$ pour tout $\scriptstyle\ k,\quad$ et $\scriptstyle\ \quad p_{k,k-1}=1-p=q,\quad$ pour $\scriptstyle\ k\ge 1,\quad$ $\scriptstyle\ \quad p_{0,0}=q.\quad$ Ce modèle est étroitement lié à l'étude des files d'attente M/M/1. La marche aléatoire réfléchie est

irréductible pour $\scriptstyle\ 0<p<1,\quad$
récurrente positive pour $\scriptstyle\ 0<p<0.5,\quad$ de loi stationnaire $\scriptstyle\ \pi_k=(1-\rho)^k\rho,\quad\rho=(q-p)/q,$
récurrente nulle pour $\scriptstyle\ p=0.5,\quad$
transiente pour $\scriptstyle\ p>0.5.\quad$

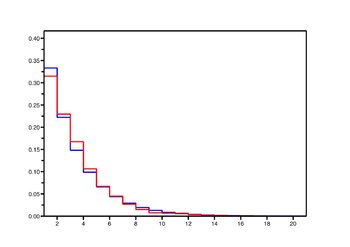
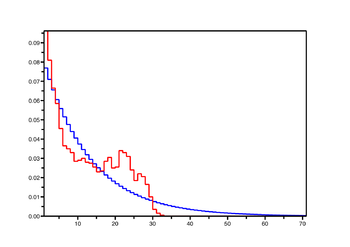
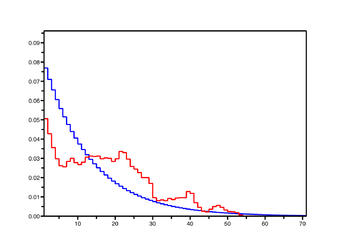
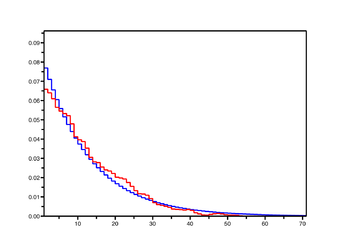
On a dessiné ci-contre des exemples de distributions empiriques et de distributions stationnaires pour la marche réfléchie en 0, pour $\scriptstyle\ \rho>0\quad$ : il semble que la convergence de l'une vers l'autre soit de plus en plus lente lorsque $\scriptstyle\ \rho\quad$ tend vers 0, i.e. quand on se rapproche des cas récurrents nuls et transients.

Chaînes réversibles

Critères

Théorème — 1. Si $\scriptstyle\ \mu=(\mu_i)_{i\in E}\qquad$ est une mesure de masse $\scriptstyle\ \Vert\mu\Vert\$ finie $\scriptstyle\ (\Vert\mu\Vert=\sum_{i\in E}\mu_i<+\infty)\qquad$ satisfaisant

$\forall i,j\in E,\qquad \mu_ip_{i,j} = \mu_jp_{j,i} ,$

alors $\scriptstyle\ \pi=\mu/\Vert\mu\Vert\quad$ est une probabilité stationnaire.

2. Plus généralement, si pour une mesure de masse finie $\scriptstyle\ \mu=(\mu_i)_{i\in E}\qquad$ il existe une matrice de transition $\scriptstyle\ (q_{i,j})_{i,j\in E}\qquad$ satisfaisant

$\forall i,j\in E,\qquad \mu_ip_{i,j} = \mu_jq_{j,i} ,$

alors $\scriptstyle\ \pi=\mu/\Vert\mu\Vert\quad$ est une probabilité stationnaire.

3. Si $\scriptstyle\ \pi\quad$ est une probabilité stationnaire, associée à la matrice de transition $\scriptstyle\ (p_{i,j})_{i,j\in E},\qquad$ telle que $\scriptstyle\ \forall i\in E,\qquad\pi_i>0,\qquad$ alors $\scriptstyle\ (q_{i,j})_{i,j\in E},\qquad$ définie par

$q_{i,j} = \frac{\pi_jp_{j,i}}{\pi_i},$

est une matrice de transition.

Démonstration

1. et 2. $\begin{align}(\mu\,P)_j&= \sum_{i\in E}\mu_ip_{i,j}\\ &= \sum_{i\in E}\mu_jq_{j,i}\\ &= \mu_j\sum_{i\in E}q_{j,i}\\ &= \mu_j,\end{align}$

la dernière égalité découlant de ce qu'une matrice de transition (par exemple $\scriptstyle\ (q_{i,j})_{i,j\in E}\qquad$ ) est une matrice stochastique. Donc μ et π sont des vecteurs propres à gauche de P, associés à la valeur propre 1, CQFD. (Nota : 1. est un cas particulier de 2.)

3. Vérifions que $\scriptstyle\ (q_{i,j})_{i,j\in E}\qquad$ ) est une matrice stochastique : pour tout i dans E,

$\begin{align}\sum_{j\in E}q_{i,j}&= \sum_{j\in E}\frac{\pi_jp_{j,i}}{\pi_i}\\ &= \frac{1}{\pi_i}\ \sum_{j\in E}\pi_jp_{j,i}\\ &=1.\end{align}$

Interprétation

Si une variable aléatoire $\scriptstyle\ X =(X_t)_{t\in \mathbb{Z}}\$ à valeur dans $\scriptstyle\ E^{ \mathbb{Z}}$ satisfait, pour tout $\scriptstyle\ (t,n)\in\mathbb{Z}\times\mathbb{N},\$ et toute suite $\scriptstyle\ (i_0,i_1,\dots,i_n)\in E^{n+1},\$

$\mathbb{P}\left((X_t,X_{t+1},\dots,X_{t+n})=(i_0,i_1,\dots,i_n)\right)= \pi_{i_0}p_{i_0,i_1}\dots p_{i_{n-1},i_n}$

on dit que X est une chaîne de Markov stationnaire, de matrice de transition $\scriptstyle\ (p_{i,j})_{i,j\in E},\qquad$ et de loi stationnaire $\scriptstyle\ (\pi_i)_{i\in E}.$ En effet :

cela définit une et une seule mesure de probabilité sur $\scriptstyle\ E^{ \mathbb{Z}}$ ;
X possède la propriété de Markov faible ;
stationnarité : la suite $\scriptstyle\ X^{(s)} =(X^{(s)}_t)_{t\in \mathbb{Z}}\$ (définie par $\scriptstyle\ X^{(s)}_t =X_{s+t}\$ ) a même loi que la suite X, pour tout entier relatif s.

Renversons le cours du temps, i.e. considérons la suite $\scriptstyle\ Y =(Y_t)_{t\in \mathbb{Z}}\$ définie par

Y t = X - t .

On a alors

Proposition —

Y est une chaîne de Markov stationnaire, de matrice de transition $\scriptstyle\ (q_{i,j})_{i,j\in E},\qquad$ (définie au point 3 ci-dessus) et de loi stationnaire $\scriptstyle\ (\pi_i)_{i\in E}.$

Si $\scriptstyle\ (q_{i,j})_{i,j\in E}=(p_{i,j})_{i,j\in E},\$ ou, de manière équivalente, si $\pi_ip_{i,j}\equiv\pi_jp_{j,i},\$ alors X et Y ont même loi. On dit que ces deux chaînes de Markov sont réversibles.

Démonstration

$\pi_{i_n}p_{i_n,i_{n-1}}\dots p_{i_{1},i_0}= \pi_{i_0}q_{i_0,i_1}\dots q_{i_{n-1},i_n},$

$\begin{align}\mathbb{P}\left((Y_t,Y_{t+1},\dots,Y_{t+n})=(i_0,i_1,\dots,i_n)\right)&= \mathbb{P}\left((X_{-t-n},X_{-t-n+1},\dots,X_{-t})=(i_n,i_{n-1},\dots,i_0)\right)\\&= \pi_{i_n}p_{i_n,i_{n-1}}\dots p_{i_{1},i_0}.\end{align}$

Graphe de la marche du cavalier sur l'échiquier (quart Sud-Ouest), et degré des sommets

Exemples

Marche aléatoire sur un graphe

Soit G un graphe connexe, fini, simple et sans boucles. Par définition,

$\forall i,j\in E=V(G),\text{ tels que }i\sim j,\qquad p_{i,j} = \frac1{d_i},$

i.e. à partir de $\scriptstyle\ i,\quad$ on saute vers un de ses $\scriptstyle\ d_i\quad$ voisins choisis au hasard (avec équiprobabilité), $\scriptstyle\ d_i\quad$ désignant le degré de $\scriptstyle\ i\quad$ dans le graphe $\scriptstyle\ G.\quad$ La connexité de $\scriptstyle\ G\quad$ entraîne l'irréductibilité de la marche aléatoire et l'unicité de la probabilité stationnaire. On remarque que $\scriptstyle\ \mu_i=d_i\qquad$ satisfait le critère 2, or $\scriptstyle\ \Vert\mu\Vert=2\vert E(G)\vert,\qquad$ i.e. $\scriptstyle\ \Vert\mu\Vert\qquad$ est deux fois le nombre d'arêtes de $\scriptstyle\ G.\qquad$ Ainsi $\scriptstyle\ \pi_i=d_i/(2\vert E(G)\vert)\qquad$ est l'unique probabilité stationnaire : on passe d'autant plus de temps en un sommet que son degré est élevé, et ce temps de séjour asymptotique est proportionnel au degré du sommet, avec coefficient de proportionnalité $\scriptstyle\ 1/(2\vert E(G)\vert).\qquad$ 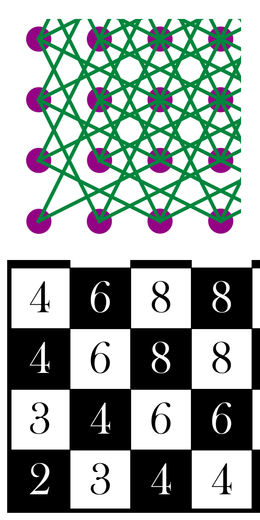Un exemple amusant est la marche aléatoire d'un cavalier sur un échiquier.

Marche du cavalier sur l'échiquier

C'est un cas particulier de l'exemple ci-dessus, où $\scriptstyle\ 2\le d_i\le 8,\ \vert V(G)\vert=|E|=64,\quad$ et $\scriptstyle\ \Vert\mu\Vert=2\vert E(G)\vert=336.\$ Ainsi

$\pi_{\text{coin SO}} = \frac{2}{336}\quad\text{et}\quad\mathbb{E}_{\text{coin SO}}\left[T_{\text{coin SO}}\right]=168,$

c'est-à-dire qu'il faut en moyenne 168 sauts à un cavalier partant du coin Sud-Ouest pour y retourner. On peut étudier de la même manière les autres pièces du jeu d'échecs.

Modèle des urnes d'Ehrenfest

Deux chiens (disons A et B) se partagent N puces de la manière suivante : à chaque instant t entier, une des N puces est tirée au hasard et change alors de chien. Notons X_t le nombre de puces infestant A au temps t : X=(X_t )_t≥0 est une chaîne de Markov en vertu du critère fondamental. Supposons que dans l'état initial, le chien A n'a aucune puce.

Cette chaîne de Markov est clairement irréductible. Si on la suppose réversible, on doit avoir

$\frac{\pi_{k+1}}{\pi_{k}}\ =\ \frac{p_{k,k+1}}{p_{k+1,k}}\ =\ \frac{N-k}{k+1}\ =\ \frac{{N\choose k+1}}{{N\choose k}},$

ce qui suggère une probabilité stationnaire, π = (π_k )_0≤k≤N , proportionnelle aux coefficients binomiaux. La seule loi de probabilité proportionnelle aux coefficients binomiaux est la loi binomiale de paramètre 1/2 (et N). La chaîne est donc bien réversible, et le temps écoulé entre deux passages par l'état initial est

$\mathbb{E}_{0}\left[T_{0}\right]\ =\ \frac1{\pi_{0}}\ =\ 2^N.$

Cet exemple illustre la réponse de Boltzmann à Zermelo : Zermelo observait^[1] une contradiction entre le théorème de récurrence de Poincaré^[2]^,^[3], selon lequel un système dynamique repasse infiniment souvent par un état donné, et le Théorème H de Boltzmann. La réponse de Boltzmann^[4] consiste à estimer le temps de récurrence moyen : pour un gaz macroscopique contenant $\scriptstyle\ N \gg 1$ molécules, Boltzmann estime celui-ci d'ordre $\scriptstyle\ 10^N$ , une durée qui est largement supérieure à l'âge de l'univers^[5] lorsque $\scriptstyle\ N \sim \mathcal{N}_A = 6.02 \ 10^{+23}$ ; les récurrences sont donc invisibles à notre échelle.

Théorie spectrale (cas fini)

On suppose

l'espace d'états E fini, à N éléments,
la chaîne réversible,
chaque π_i strictement positif.

Alors^[6]

Théorème — La matrice de transition P est diagonalisable à gauche dans une base orthonormée pour la distance du χ² , i.e. dans une base orthonormée pour la forme bilinéaire

$\langle x,y\rangle\ =\ \sum_{i=1}^N\, \frac{x_i\,y_i}{\pi_i}.$

Ses valeurs propres à gauche sont réelles et de valeurs absolues inférieures à 1.

Démonstration

Notons D la matrice diagonale de terme diagonal général $\scriptstyle\ \sqrt{\pi_i}.\$ Alors S = D.P.D^-1 est une matrice symétrique, semblable à P. En effet

$S_{i,j}\ =\ \frac{\sqrt{\pi_i}\,p_{i,j}}{\sqrt{\pi_j}}\ =\ \frac{\sqrt{\pi_j}\,p_{j,i}}{\sqrt{\pi_i}}\ =\ S_{j,i}.$

En vertu du théorème spectral, on conclut donc que S est diagonalisable en base orthonormée, et n'a que des valeurs propres réelles. Si u et v sont deux vecteurs propres à gauches de S, orthogonaux (i.e. u.^tv = 0 ), alors les vecteurs propres correspondants de P sont x = u.D et y = v.D. On a donc

$0\ =\ u.^tv\ =\ x.D^{-2}.^ty\ =\ \sum_{i=1}^N\, \frac{x_i\,y_i}{\pi_i}.$

L'encadrement des valeurs propres découle des deux relations :

$u\left(\text{Id}-DPD^{-1}\right)\,^tu\ =\ \tfrac12\ \sum_{1\le i,j\le N}\,\pi_ip_{i,j}\,\left(\tfrac{u_i}{\pi_i}-\tfrac{u_j}{\pi_j}\right)^2,$

$u\left(\text{Id}+DPD^{-1}\right)\,^tu\ =\ \tfrac12\ \sum_{1\le i,j\le N}\,\pi_ip_{i,j}\,\left(\tfrac{u_i}{\pi_i}+\tfrac{u_j}{\pi_j}\right)^2.$

En effet, les termes de droites de ces égalités sont positifs ou nuls. Si λ est une valeur propre quelconque de P, v un vecteur propre à gauche associé, et si on choisit u = vD^-1 , alors les termes de gauche sont $\scriptstyle\ (1-\lambda)\Vert u\Vert^2\$ et $\scriptstyle\ (1+\lambda)\Vert u\Vert^2, \$ respectivement. D'où l'encadrement annoncé.

Cas d'égalité. Si u est une probabilité stationnaire de la chaîne, alors, dans la première relation ci-dessus, la somme de droite est nulle, donc tout ses termes (qui sont positifs ou nuls) sont nuls. Cela entraine que la fraction u_j /π_j reste constante le long de n'importe quel chemin du graphe de la chaîne. Si la chaîne est irréductible, il suit que u est proportionnelle à π, donc égale à π. Ainsi il existe une seule probabilité stationnaire.

Une discussion analogue concernant la deuxième égalité permet de conclure à l'existence d'un vecteur propre pour la valeur propre -1 si et seulement si la chaîne est de période 2.

Convergence pour la distance du χ²

Si la chaîne est irréductible et apériodique, 1 est valeur propre de P de multiplicité 1, et les autres valeurs propres sont en valeur absolue strictement inférieures à 1. Si on note α le maximum de ces valeurs absolues et si on note μ_n la loi de la chaîne au temps n, on en déduit^[6] que

$\langle \mu_n-\pi,\mu_n-\pi\rangle\ \le\ C\,\alpha^{2n}.$

Si l'erreur relative, au site i, est définie par

$\varepsilon_i=\frac{\mu_{n,i}-\pi_i}{\pi_i},$

alors la distance du χ² entre μ_n et π s'écrit

$\langle \mu_n-\pi,\mu_n-\pi\rangle\ =\ \sum_{i=1}^N\,\pi_i\,\varepsilon_i^2.$

Ainsi les erreurs relatives sont moins pénalisantes si elles affectent les états les moins probables mais sont, toutefois, plus pénalisantes que si on utilise la distance euclidienne classique :

$\Vert\mu_n-\pi\Vert^2\ =\ \sum_{i=1}^N\,(\mu_{n,i}-\pi_i)^2\ =\ \sum_{i=1}^N\,\pi_i^2\,\varepsilon_i^2.$

Théorie spectrale (cas du modèle des urnes d'Ehrenfest)

Théorème — La matrice de transition P possède N+1 valeurs propres distinctes :

$1=\lambda_{0}\ge\lambda_{1}\ge\dots\ge\lambda_{k}=\tfrac{N-2k}N\ge\dots\ge\lambda_{N}=-1.$

Le vecteur e_k défini par

$(1-X)^{k}(1+X)^{N-k}\,=\,\sum_{j=0}^{N}\ e_{k,j}X^{j}$

est un vecteur propre à gauche de P associé à la valeur propre λ_k .

Démonstration

On considère l'opérateur T défini sur les suites de nombres réels par

$(Tu)_{k}\,=\,\tfrac{N-k+1}N\,u_{k-1}+\tfrac{k+1}N\,u_{k+1},\quad k\ge 0,$

avec la convention u_-1 =0. Supposons que λ soit une valeur propre de T et notons u un vecteur propre associé. Posons

$F(X)\,=\,\sum_{k\ge 0}\,u_{k}X^{k}.$

Alors on devrait avoir

$\begin{align} \lambda F(X)&=\sum_{k\ge 0}\,\left(\tfrac{N-k+1}N\,u_{k-1}+\tfrac{k+1}N\,u_{k+1}\right)X^{k} \\ &=X\sum_{k\ge 0}\,\,u_{k-1}X^{k-1}-\tfrac{X^{2}}N\sum_{k\ge 0}\,(k-1)\,u_{k-1}X^{k-2}+\,\tfrac{1}N\,\sum_{k\ge 0}\,(k+1)\,u_{k+1}X^{k} \\ &=XF(X)-\tfrac{X^{2}}N\,F^{\prime}(X)+\,\tfrac{1}N\,F^{\prime}(X) \\ &=XF(X)+\tfrac{1-X^{2}}N\,F^{\prime}(X). \end{align}$

Il faudrait donc (formellement) que

$\begin{align} \tfrac2N\,\frac{F^{\prime}(X)}{F(X)}&=2\ \frac{\lambda -X}{1-X^{2}} \\ &=\frac{\lambda -1}{1-X}+\frac{\lambda +1}{1+X}. \end{align}$

ou encore que

$F(X)\ =\ C\,(1-X)^{(1-\lambda)N/2}\ (1+X)^{(\lambda +1)N/2}.$

Par ailleurs, si v=(v₀ ,v₁ , ... ,v_N ) est un vecteur ligne et si u désigne la suite obtenue en complétant v par une suite infinie de 0's, alors

$vP\ =\ Tu,$

et la série génératrice F associée à u est un polynome de degré inférieur à N. Ainsi les valeurs de λ pour lesquelles l'expression de F donnée ci-dessus est un polynome (nécessairement de degré N car N est la somme des exposants) sont non seulement des valeurs propres de T, mais aussi des valeurs propres de P. Or si 1-λ est de la forme 2k/N (où k désigne un entier naturel) alors l'exposant de (1-X) est un entier naturel et l'exposant de (1+X) est un entier relatif. Si, de plus, k≤N, alors le deuxième exposant est un entier naturel. Cela fait à P autant de valeurs propres distinctes qu'il y a d'entiers entre 0 et N, soit N+1 valeurs propres, au moins. Mais la matrice P, de dimension N+1, ne peut avoir plus de N+1 valeurs propres. On a donc trouvé toutes les valeurs propres, et leurs vecteurs propres à gauche associés. Ce calcul est tiré d'un article de Mark Kac^[7].

Ainsi, il y a convergence vers la loi stationnaire uniquement si la loi initiale μ est orthogonale à e_N , i.e. si

$\sum_{i=0}^N\,(-1)^i\,\mu_i=0.$

En ce cas, il existe une constante C_N telle que, pour tout entier naturel k, on ait :

$\Vert\mu.P^k-\pi\Vert\le C_N\,\left(1-\tfrac2N\right)^k.$

Existence et unicité

Graphe d'une chaîne de Markov non irréductible à espace d'états fini, possédant 3 classes : $\scriptstyle\ \{1,3\}\ \leftarrow\ \{2\}\$ et $\scriptstyle\ \{4,5\}.\$

Discuter l'existence et l'unicité d'une probabilité stationnaire $\scriptstyle\ \pi\$ telle que $\scriptstyle\ \pi_i>0\$ amène à discuter les propriétés du graphe de la chaîne de Markov et la classification de ses états, amène aussi à étudier les propriétés de la variable aléatoire appelée "temps de retour" en $\scriptstyle\ i,\$ et souvent notée $\scriptstyle\ T_i.\quad$

Théorème — On a équivalence entre les 2 propositions suivantes

L'état $\scriptstyle\ i\quad$ est récurrent positif,
il existe une probabilité stationnaire $\scriptstyle\ \pi\$ telle que $\scriptstyle\ \pi_i>0.\$

Si l'une des deux conditions précédentes est remplie, alors

la classe $\scriptstyle\ C\quad$ de l'état $\scriptstyle\ i\quad$ est une classe finale,
le support de $\scriptstyle\ \pi\quad$ contient $\scriptstyle\ C,\quad$
tous les éléments de $\scriptstyle\ C\quad$ sont récurrent positifs,
$\scriptstyle\ \pi_i\mathbb{E}_i\left[T_i\right]\le 1.\quad$

De plus, il y a équivalence entre

le support de $\scriptstyle\ \pi\quad$ est exactement $\scriptstyle\ C,\quad$ i.e. $\scriptstyle\ \{\pi_j>0\}\Leftrightarrow\{j\in C\},$
$\scriptstyle\ \pi_i\mathbb{E}_i\left[T_i\right]= 1,\quad$
$\scriptstyle\ \pi\quad$ est un point extrémal de l'ensemble (convexe) des probabilités stationnaires.

En particulier, si une chaîne de Markov possède au moins un état récurrent positif, alors il existe une probabilité stationnaire.

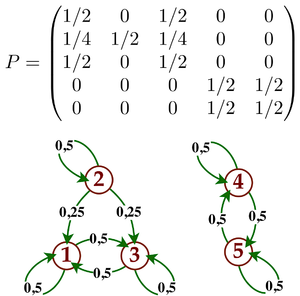
Exemple :

Pour la chaîne dont le graphe est représenté ci-dessus, l'ensemble des probabilités stationnaires est le segment dont les extrémités, correspondant aux deux classes finales $\scriptstyle\ C=\{1,3\}\$ et $\scriptstyle\ C^{\prime}=\{4,5\},\$ sont $\scriptstyle\ \pi_C=\left(\tfrac12,0,\tfrac12,0,0\right)$ et $\scriptstyle\ \pi_{C^{\prime}}=\left(0,0,0,\tfrac12,\tfrac12\right).$ Une probabilité stationnaire est nécessairement de la forme $\scriptstyle\ \pi=\left(\alpha,0,\alpha,\beta,\beta\right),\quad\alpha+\beta=0.5.$

Corollaire — Si une chaîne de Markov possède une seule classe finale $\scriptstyle\ C,\$ alors il existe au plus une probabilité stationnaire. On a alors équivalence entre les 3 propositions :

il existe une probabilité stationnaire,
il existe un état récurrent positif,
tous les états de la classe finale sont récurrents positifs.

Supposons qu'une des 3 conditions ci-dessus soit remplie et notons $\scriptstyle\ \pi\quad$ l'unique probabilité stationnaire : alors

$\forall i\in E,\quad \pi_i\ =\ \frac1{\mathbb{E}_i\left[T_i\right]},$

et on a la série d'équivalences

$\{\pi_i>0\}\Leftrightarrow\{i\in C\}\Leftrightarrow\{i\text{ est recurrent positif}\}.$

Ce théorème vaut en particulier pour les chaînes de Markov irréductibles, puisque ces dernières possèdent une seule classe (qui est donc nécessairement une classe finale) ; les chaînes de Markov irréductibles vérifient en particulier $\scriptstyle\ C=E.$

A voir

Notes

↑ Ernst Zermelo ; Uber einen Satz der Dynamik une der mechanischen Wärmetheorie, Wied. Ann. 57 (1896), 793.
↑ Henri Poincaré ; Sur le problème des trois corps et les équations de la dynamique, Acta Mathamatica 13 (1890), 1-270.
↑ Ludwig Boltzmann ; Uber einen mechanischen Satz von Poincaré, Wien. Ber. 106 (1897), 12.
↑ Ludwig Boltzmann ; Entgegnung auf die wärmetheoretische Betrachtung des Herrn Zermelo, Wied. Ann. \textbf{57} (1896), 773 ; et : \textbf{60} (1897), 392.
↑ Environ 15 milliards d'années.
↑ ^{a et b} Bernard Ycart, Modèles et algorithmes Markoviens, p.127-130.
↑ Mark Kac, Random Walk and the Theory of Brownian Motion, American Mathematical Monthly 54(7) (1947), 369-391. Texte au format pdf.

Bibliographie

Laurent Saloff-Coste, Lectures on finite Markov chains, Lectures on Probability Theory and Statistics, 301-413. Lecture Notes in Math. n° 1665. Springer (1997).
Jim Norris, Markov chains.
Samuel Karlin et Howard E. Taylor, A Second Course in Stochastic Processes.

Pages liées

Portail des probabilités et des statistiques

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Probabilité stationnaire d'une chaîne de Markov de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Récurrence et transience d'une chaîne de Markov — Un état d une chaîne de Markov est dit récurrent si une trajectoire « typique » de la chaîne de Markov passe par une infinité de fois, sinon l état est dit transient. Ces propriétés de transience ou de récurrence sont souvent partagées… … Wikipédia en Français
Chaine De Markov — Chaîne de Markov Selon les auteurs, une chaîne de Markov est de manière générale un processus de Markov à temps discret ou un processus de Markov à temps discret et à espace d états discret. En mathématiques, un processus de Markov est un… … Wikipédia en Français
Chaine de Markov — Chaîne de Markov Selon les auteurs, une chaîne de Markov est de manière générale un processus de Markov à temps discret ou un processus de Markov à temps discret et à espace d états discret. En mathématiques, un processus de Markov est un… … Wikipédia en Français
Chaine de markov — Chaîne de Markov Selon les auteurs, une chaîne de Markov est de manière générale un processus de Markov à temps discret ou un processus de Markov à temps discret et à espace d états discret. En mathématiques, un processus de Markov est un… … Wikipédia en Français
Chaîne De Markov — Selon les auteurs, une chaîne de Markov est de manière générale un processus de Markov à temps discret ou un processus de Markov à temps discret et à espace d états discret. En mathématiques, un processus de Markov est un processus stochastique… … Wikipédia en Français
Chaîne de Markov à espace d'états discret — Chaîne de Markov Selon les auteurs, une chaîne de Markov est de manière générale un processus de Markov à temps discret ou un processus de Markov à temps discret et à espace d états discret. En mathématiques, un processus de Markov est un… … Wikipédia en Français
Chaîne de markov — Selon les auteurs, une chaîne de Markov est de manière générale un processus de Markov à temps discret ou un processus de Markov à temps discret et à espace d états discret. En mathématiques, un processus de Markov est un processus stochastique… … Wikipédia en Français
Chaîne de Markov — Selon les auteurs, une chaîne de Markov est de manière générale un processus de Markov à temps discret ou un processus de Markov à temps discret et à espace d états discret. En mathématiques, un processus de Markov est un processus stochastique… … Wikipédia en Français
Graphe d'une chaîne de Markov — et classification des états Le graphe d une chaîne de Markov et la classification des états sont des notions de la théorie des graphes utilisées en calcul des probabilités. Sommaire 1 Graphe d une chaîne de Markov 2 Classification des états … Wikipédia en Français
Graphe d'une chaîne de Markov et classification des états — Le graphe d une chaîne de Markov et la classification des états sont des notions de la théorie des graphes utilisées en calcul des probabilités. Sommaire 1 Graphe d une chaîne de Markov 2 Classification des états 3 Lexi … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Probabilité stationnaire d'une chaîne de Markov

Sommaire

Définition

Existence et unicité : cas irréductible

Loi forte des grands nombres

Ergodicité

Convergence vers la loi stationnaire

Convergence de la loi marginale

Convergence de la mesure empirique

Chaînes réversibles

Critères

Interprétation

Exemples

Marche aléatoire sur un graphe

Marche du cavalier sur l'échiquier

Modèle des urnes d'Ehrenfest

Théorie spectrale (cas fini)

Convergence pour la distance du χ²

Théorie spectrale (cas du modèle des urnes d'Ehrenfest)

Existence et unicité

A voir

Notes

Bibliographie

Pages liées

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Probabilité stationnaire d'une chaîne de Markov

Sommaire

Définition

Existence et unicité : cas irréductible

Loi forte des grands nombres

Ergodicité

Convergence vers la loi stationnaire

Convergence de la loi marginale

Convergence de la mesure empirique

Chaînes réversibles

Critères

Interprétation

Exemples

Marche aléatoire sur un graphe

Marche du cavalier sur l'échiquier

Modèle des urnes d'Ehrenfest

Théorie spectrale (cas fini)

Convergence pour la distance du χ2

Théorie spectrale (cas du modèle des urnes d'Ehrenfest)

Existence et unicité

A voir

Notes

Bibliographie

Pages liées

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link

Convergence pour la distance du χ²