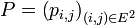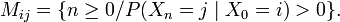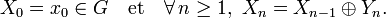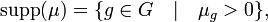- Graphe d'une chaîne de Markov
-
Graphe d'une chaîne de Markov et classification des états
Le graphe d'une chaîne de Markov et la classification des états sont des notions de la théorie des graphes utilisées en calcul des probabilités.
Sommaire
Graphe d'une chaîne de Markov
Le graphe
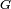 d'une chaîne de Markov est un graphe orienté défini à partir de l'espace d'états
d'une chaîne de Markov est un graphe orienté défini à partir de l'espace d'états 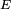 et de la matrice de transition
et de la matrice de transitionde cette chaîne de Markov :
- les sommets de
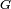 sont les éléments de
sont les éléments de 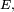
- les arêtes de
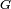 sont les couples
sont les couples 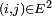 vérifiant
vérifiant
- pi,j > 0.
Classification des états
Pour
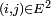 , on dit que
, on dit que 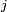 est accessible à partir de
est accessible à partir de  si et seulement s'il existe
si et seulement s'il existe 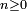 tel que
tel que 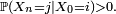 On note :
On note :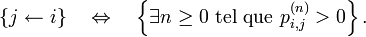
On dit que
 et
et 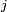 communiquent si et seulement s'il existe
communiquent si et seulement s'il existe 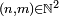 tels que
tels que 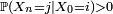 et
et 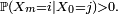 On note :
On note :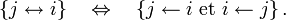
La relation communiquer, notée
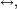 est une relation d'équivalence. Quand on parle de classe en parlant des états d'une chaîne de Markov, c'est général aux classes d'équivalence pour la relation
est une relation d'équivalence. Quand on parle de classe en parlant des états d'une chaîne de Markov, c'est général aux classes d'équivalence pour la relation  qu'on fait référence. Si tous les états communiquent, la chaîne de Markov est dite irréductible.
qu'on fait référence. Si tous les états communiquent, la chaîne de Markov est dite irréductible.La relation être accessible, notée
 s'étend aux classes d'équivalence : pour deux classes
s'étend aux classes d'équivalence : pour deux classes 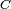 et
et 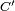 , on a
, on a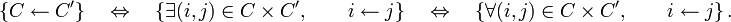
La relation
 est une relation d'ordre entre les classes d'équivalence.
est une relation d'ordre entre les classes d'équivalence.
Une classe est dite finale si elle ne conduit à aucune autre, i.e. si la classe est minimale pour la relation Sinon, la classe est dite transitoire.
Sinon, la classe est dite transitoire.Soit
La période d'un état
 est le PGCD de l'ensemble
est le PGCD de l'ensemble 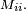 Si deux états communiquent, ils ont la même période : on peut donc parler de la période d'une classe d'états. Si la période vaut 1, la classe est dite apériodique.
Si deux états communiquent, ils ont la même période : on peut donc parler de la période d'une classe d'états. Si la période vaut 1, la classe est dite apériodique.La classification des états se lit de manière simple sur le graphe de la chaîne de Markov.
Marche aléatoire sur un groupe fini :On se donne un groupe
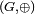 et une mesure de probabilité
et une mesure de probabilité  sur ce groupe, ainsi qu'une suite
sur ce groupe, ainsi qu'une suite 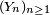 de variables aléatoires indépendantes de loi
de variables aléatoires indépendantes de loi 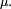 On pose
On poseAlors
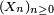 est appelée marche aléatoire de pas
est appelée marche aléatoire de pas  sur le groupe
sur le groupe 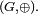 Le processus stochastique
Le processus stochastique 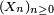 est un processus de Markov. C'est une chaîne de Markov si
est un processus de Markov. C'est une chaîne de Markov si 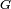 est fini ou dénombrable (en ce cas
est fini ou dénombrable (en ce cas 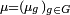 ). Notons
). Notons 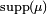 le support de
le support de  :
:et notons
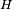 le sous-groupe engendré par
le sous-groupe engendré par 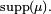 Alors les classes à droite modulo
Alors les classes à droite modulo 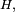 (de type
(de type 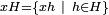 ) sont aussi les classes pour la relation
) sont aussi les classes pour la relation 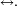 Ces classes sont toutes finales.Marches sur le cube :
Ces classes sont toutes finales.Marches sur le cube :- La marche aléatoire sur les arètes du cube peut être vue comme la marche sur le groupe
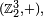 de pas
de pas 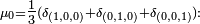 en effet ajouter un des 3 vecteurs de la base canonique revient à changer une des trois coordonnées du point de départ, i.e. cela revient à emprunter, au hasard, une des 3 arètes issues du point de départ. En ce cas
en effet ajouter un des 3 vecteurs de la base canonique revient à changer une des trois coordonnées du point de départ, i.e. cela revient à emprunter, au hasard, une des 3 arètes issues du point de départ. En ce cas 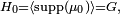 et la marche est irréductible.
et la marche est irréductible. - Si le pas est
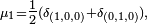
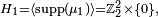 et la marche a deux classes finales : les 2 faces horizontales.
et la marche a deux classes finales : les 2 faces horizontales. - Si le pas est
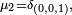
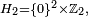 et la marche a 4 classes finales : les 4 arètes verticales.
et la marche a 4 classes finales : les 4 arètes verticales. - Si le pas est
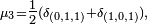
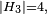 et la marche a deux classes finales : les 2 tétraèdres inscrits.
et la marche a deux classes finales : les 2 tétraèdres inscrits.
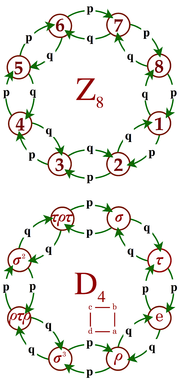 Graphe de 2 marches aléatoires élémentaires, respectivement sur le groupe cyclique
Graphe de 2 marches aléatoires élémentaires, respectivement sur le groupe cyclique
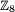 et sur le groupe diédral
et sur le groupe diédral 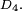 Marches aléatoires sur l'octogone :
Marches aléatoires sur l'octogone :- La 1ère chaîne de Markov de la figure ci-contre est une marche aléatoire sur le groupe cyclique
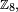 de pas
de pas 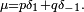 Dans cet exemple,
Dans cet exemple, 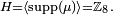
- La 2ème chaîne de Markov de la figure ci-contre est une marche aléatoire sur le groupe diédral
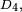 de pas
de pas 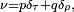 où
où 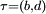 est la symétrie du carré (abcd) par rapport à la diagonale (a,c), où
est la symétrie du carré (abcd) par rapport à la diagonale (a,c), où 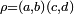 est la symétrie du carré par rapport à son axe horizontal, les deux autres symétries étant
est la symétrie du carré par rapport à son axe horizontal, les deux autres symétries étant 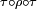 et
et 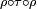 ;
; 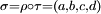 est la rotation d'angle
est la rotation d'angle 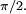 Dans cet exemple,
Dans cet exemple, 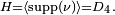
Les deux chaînes sont donc irréductibles et récurrentes positives, de loi stationnaire uniforme.
Lexique : graphes-chaînes de Markov
- L'état
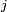 est accessible à partir de l'état
est accessible à partir de l'état  si et seulement si l'une des deux conditions suivantes est remplie :
si et seulement si l'une des deux conditions suivantes est remplie :
- il existe un chemin allant du sommet
 au sommet
au sommet 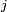 dans le graphe
dans le graphe 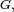
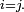
- il existe un chemin allant du sommet
- Une chaîne de Markov est irréductible si et seulement si son graphe est fortement connexe, i.e. si pour tout couple
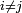 de sommets du graphe il existe un chemin de
de sommets du graphe il existe un chemin de  à
à 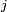 et un chemin de
et un chemin de 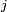 à
à 
- Une classe d'une chaîne de Markov est une composante fortement connexe de son graphe. Dans l'exemple ci-dessus le graphe non orienté induit par le graphe de la chaîne de Markov a 2 composantes connexes, mais le graphe de la chaîne de Markov (qui est un graphe orienté) a 3 composantes fortement connexes, car 2 ne communique ni avec 1, ni avec 3.
Graphe d'une chaîne de Markov et propriétés probabilistes
Certaines propriétés probabilistes des états d'une chaîne de Markov sont partagées par tous les états d'une même classe. Plus précisément:
- si une classe
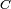 n'est pas finale, tous ses états sont transients (ou transitoires),
n'est pas finale, tous ses états sont transients (ou transitoires), - si une classe
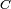 est à la fois finale et finie, tous ses états sont récurrents positifs.
est à la fois finale et finie, tous ses états sont récurrents positifs.
Par ailleurs,
- s'il existe
 récurrent dans la classe
récurrent dans la classe 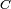 , alors tout état
, alors tout état 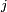 de
de 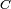 est récurrent,
est récurrent, - s'il existe
 récurrent positif dans la classe
récurrent positif dans la classe 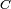 , alors tout état
, alors tout état 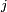 de
de 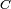 est récurrent positif,
est récurrent positif, - s'il existe
 récurrent nul dans la classe
récurrent nul dans la classe 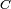 , alors tout état
, alors tout état 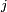 de
de 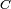 est récurrent nul,
est récurrent nul, - s'il existe
 transient dans la classe
transient dans la classe 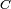 , alors tout état
, alors tout état 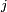 de
de 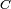 est transient,
est transient, - s'il existe
 de période
de période  dans la classe
dans la classe 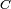 , alors tout état
, alors tout état 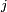 de
de 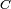 est de période
est de période 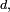
- s'il existe
 apériodique dans la classe
apériodique dans la classe 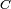 , alors tout état
, alors tout état 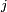 de
de 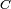 est apériodique.
est apériodique.
On dit donc que la classe
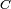 est transiente, récurrente, apériodique, etc ... puisqu'il s'agit en fait de propriétés de la classe tout autant que de propriétés d'un état particulier.
est transiente, récurrente, apériodique, etc ... puisqu'il s'agit en fait de propriétés de la classe tout autant que de propriétés d'un état particulier.Les états d'une classe finale peuvent très bien être tous transients (par exemple dans le cas de la marche simple biaisée sur
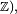 ou bien être tous récurrents nuls (par exemple dans le cas de la marche simple symétrique sur
ou bien être tous récurrents nuls (par exemple dans le cas de la marche simple symétrique sur 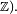 Tout au plus faut-il pour cela que la classe finale en question soit infinie. Il existe également des exemples de classe finale infinie récurrente positive.Catégorie : Processus stochastique
Tout au plus faut-il pour cela que la classe finale en question soit infinie. Il existe également des exemples de classe finale infinie récurrente positive.Catégorie : Processus stochastique
Wikimedia Foundation. 2010.


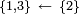 et
et 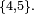 Les classes
Les classes 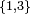 et
et 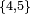 sont finales.
sont finales.