Prisme rectangulaire

Prisme rectangulaire

Cuboïde

Page d'aide sur l'homonymie Pour les articles homonymes, voir Os cuboïde.
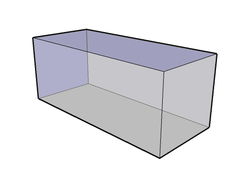
Cuboïde
Cuboïde
Type Prisme
Faces 6 rectangles
Arrêtes 12
Sommets 8
Groupe de symétrie D2h (*222)
Propriétés convexe, zonoèdre, isogone

En géométrie, un cuboïde est une figure solide délimitée par six faces rectangulaires (boîte rectangulaire). Tous les angles sont des angles droits et les faces opposées du cuboïde sont égales. C'est aussi un prisme rectangulaire droit. L'expression de « prisme rectangulaire ou oblong » est ambigüe. L'expression de parallélépipède rectangle est aussi utilisée.
Le cuboïde carré, la boîte carrée ou le prisme carré droit (aussi appelé de manière ambigüe prisme carré) est un cas particulier de cuboïde dont au moins deux faces sont carrées. Le cube est un cas particulier de cuboïde carré dont toutes les faces sont carrées.
Si les dimensions du cuboïde sont a, b et c, son volume est le produit abc et sa surface est 2(ab + ac + bc).
La longueur de la grande diagonale est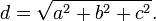 d = \sqrt{a^2+b^2+c^2} .
Le cuboïde est un polyèdre convexe. Ses six faces bornent une région unique de l'espace. Il possède 8 sommets et 12 arêtes.
La formule d'Euler F + S = A + 2 (où F = nombre de faces, S = nombre de sommets, A = nombre d'arêtes d'un polyèdre) donne ici 6 + 8 = 12 + 2.
La forme cuboïde est souvent utilisée pour les boîtes, les armoires, les pièces, les immeubles, etc. Le cuboïde fait partie des solides pouvant paver un espace tridimensionnel. Cela lui donne une grande polyvalence, puisque chaque cuboïde peut contenir des cuboïdes plus petits : une boîte à sucre contient des morceaux de sucre, un immeuble contient des pièces, etc.

Voir aussi

  • hyperrectangle

Liens externes


  • (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Cuboid ».
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Cubo%C3%AFde ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Prisme rectangulaire de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • prisme — [ prism ] n. m. • 1609; gr. prisma, prismatos, de prizein « scier » 1 ♦ Géom. Polyèdre ayant deux bases égales et parallèles et dont les faces latérales sont des parallélogrammes. Prisme triangulaire. Prisme régulier, qui a pour bases des… …   Encyclopédie Universelle

  • prisme — (pri sm ) s. m. 1°   Terme de géométrie. Polyèdre ayant pour bases deux polygones égaux et parallèles, dont les côtés homologues sont unis par des parallélogrammes. •   Cet étalon [une mesure], comme celui de Turin, est un prisme à cinq pans de… …   Dictionnaire de la Langue Française d'Émile Littré

  • Cuboide — Cuboïde Pour les articles homonymes, voir Os cuboïde. Cuboïde Type Prisme Faces 6 …   Wikipédia en Français

  • Cuboïde — Pour les articles homonymes, voir Os cuboïde. Cuboïde Type Prisme Faces 6 …   Wikipédia en Français

  • Intamin — AG Logo de Intamin Siège social Wollerau …   Wikipédia en Français

  • Intamin AG — Logo de Intamin AG Siège social Wollerau …   Wikipédia en Français

  • Parallélépipède rectangle — Cuboïde Pour les articles homonymes, voir Os cuboïde. Cuboïde Type Prisme Faces 6 …   Wikipédia en Français

  • Pavé droit — Parallélépipède rectangle Type Prisme Faces 6 rectangles Arêtes 12 Sommets 8 Groupe de …   Wikipédia en Français

  • cristalliser — [ kristalize ] v. <conjug. : 1> • 1620; de cristal 1 ♦ V. tr. Faire passer (un corps) à l état de cristaux. Cristalliser un sel par dissolution. ⇒ cristallisation. P. p. adj. Du sucre cristallisé (⇒ candi) . Pronom. « Les sels dissous dans… …   Encyclopédie Universelle

  • périorthogone — (pé ri or to go n ) adj. Terme de minéralogie. Se dit d un prisme rhomboïdal qui s est converti en un prisme rectangulaire. ÉTYMOLOGIE    Péri 3..., et orthogone …   Dictionnaire de la Langue Française d'Émile Littré

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”