Pas de solution

En mathématiques, l'ensemble vide est l'ensemble ne contenant aucun élément.

Sommaire 1 Notation 2 Propriétés 3 Difficultés de la notion d'ensemble vide 4 L'ensemble vide dans la théorie axiomatique des ensembles 5 Le point de vue catégorique 6 Voir aussi

Notation

L'ensemble vide peut être noté d'un rond barré 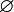ou simplement {}, deux accolades ouvrantes et fermantes ne contenant rien. La notation ∅ a été introduite par le mathématicien français André Weil du groupe Bourbaki.

À noter que l'unicode possède trois caractères distincts U+2205 (∅) pour l'ensemble vide, U+00D8 (Ø) lettre de l'alphabet danois, et U+2300 (⌀) représentant le diamètre d'un cercle. Ces trois caractères ont la forme d'un cercle barré par un trait allant du sud-ouest au nord-est. Il est plus aisé de les distinguer de la lettre Phi majuscule de l'alphabet grec (Φ), qui elle consiste en un cercle barré d'un trait vertical. Le rond barré n'est pas non plus le zéro barré.

Propriétés

• Pour tout ensemble A, l'ensemble vide est un sous-ensemble de A :

  ∀A ensemble, ∅ ⊂ A

• Pour tout ensemble A, l'union de A avec l'ensemble vide est A :

  ∀A ensemble, ∅ ∪ A = A

• Pour tout ensemble A, l'intersection de A avec l'ensemble vide est l'ensemble vide :

  ∀A ensemble, ∅ ∩ A = ∅

• Le seul sous-ensemble de l'ensemble vide est l'ensemble vide lui-même. :

  ∀A ensemble, A ⊂ ∅ ⇒ A = ∅

• Le cardinal de l'ensemble vide est zéro, en particulier l'ensemble vide est fini :

  Card(∅) = 0

• Pour tout ensemble non vide E. L'ensemble des fonctions de E dans l'ensemble vide est vide. L'ensemble des fonctions de l'ensemble vide dans E est lui un singleton.

Les mathématiciens préfèrent parler de l'ensemble vide plutôt que d'un ensemble vide. En effet, dans la théorie des ensembles, deux ensembles sont égaux s'ils contiennent les mêmes éléments : ainsi, il ne peut y avoir qu'un ensemble ne contenant aucun élément.

Difficultés de la notion d'ensemble vide

L'ensemble vide ne correspond pas à rien ; c'est en fait un ensemble qui ne contient rien, mais en tant qu'ensemble il n'est pas rien. Ce point est souvent difficile à saisir au premier abord. On peut, afin de mieux comprendre, comparer un ensemble à un sac : un sac vide est vide, mais le sac en lui-même existe.

De même, la notation {∅} n'a pas le même sens que ∅. La dernière notation décrit un ensemble qui ne contient rien alors que la première décrit un ensemble contenant un élément : l'ensemble vide. On peut, afin de mieux comprendre, reprendre l'analogie du sac vide. Un tiroir contenant un sac vide - {∅} - n'est pas vide et contient bien un objet - ∅ -.

On peut aussi être surpris par la première propriété ci-dessus, c'est-à-dire le fait que l'ensemble vide soit un sous-ensemble de n'importe quel ensemble A. D'après la définition d'un sous-ensemble, cela veut dire que pour tout élément x de ∅, x appartient à A. Raisonnons a contrario : si l'ensemble vide n'est pas inclus dans A, alors il existe au moins un élément de l'ensemble vide qui n'appartient pas à A. Or, il n'y a aucun élément dans l'ensemble vide, donc plus particulièrement aucun élément de l'ensemble vide qui n'appartienne pas à A. On en conclut donc que tout élément de ∅ appartient à A et donc que ∅ est un sous-ensemble de A. Plus généralement, toute proposition commençant par « pour tout élément de ∅ » est vraie.

L'ensemble vide dans la théorie axiomatique des ensembles

L'ensemble vide est essentiel dans la théorie des ensembles ou théorie ZFC, son existence est assurée par l'axiome de l'ensemble vide. Son unicité découle de l'axiome d'extensionnalité.

De plus, on peut démontrer en utilisant le schéma d'axiomes de compréhension, que l'existence d'un ensemble quelconque implique l'axiome de l'ensemble vide, ce qui évite, quand on formalise la théorie des ensembles en logique du premier ordre, de faire appel à un axiome spécifique pour l'existence de l'ensemble vide (voir axiome de l'ensemble vide).

Le point de vue catégorique

L'ensemble vide peut être caractérisé très simplement comme objet de la catégorie des ensembles. C'est en effet l'unique objet ayant la propriété suivante:

Pour tout ensemble E, il existe une et une seule flèche de ∅ vers E.

Dans le cas de cette catégorie, flèche signifie application. Plus généralement, un objet qui dans une catégorie a cette propriété est appelé un objet initial.

Voir aussi

• Théorie des ensembles
• Sous-ensemble
• Théorie des catégories

Articles de mathématiques en rapport avec la notion de nombre

Définition des nombres · Entiers naturels · Entiers relatifs · Nombres transfinis  · Nombres décimaux · Nombres rationnels · Nombres constructibles · Nombres algébriques · Nombres transcendants · Nombres calculables · Nombres réels · Nombres complexes · Nombres hypercomplexes · Quaternions · Octonions · Sédénions · Nombres hyperréels · Nombres surréels · Nombres ordinaux · Nombres cardinaux · Nombres p-adiques · Nombres normaux · Suite d'entiers · Constantes mathématiques · Grands nombres · Infiniments petits · Infini

• Portail des mathématiques