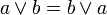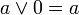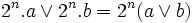Operations sur les bits

Operations sur les bits

Opérations sur les bits

Sommaire

Introduction

Dans les langages informatiques, par exemple C++, Php, Java etc. on trouve des opérations dit: « bit par bit ». l'ordinateur pour faire ce type de calcul, entre deux entiers, doit convertir les entiers vers le système binaire, faire les opérations bit par bit, puis retourner le résultat au système du départ. L'objectif de cet article est de trouver des méthodes de calcul, sans passer au système binaire, et de prolonger vers l'ensemble \mathbb{R}

Opération conjonction (et) sur les bits

La conjonction (et) entre deux entiers a et b, se représente: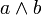a \wedge b. Dans la mesure ou les opérations logiques sur les propositions sont homogènes sur les opérations entre les ensembles finis: par exemple, il y a une relation entre la conjonction et l'intersection entre deux ensembles finis.

Présenter les entiers dans les ensembles fini

Tout nombre entier peut être relié à un ensemble fini, dont les éléments sont des entiers: exemple pour 15:
on a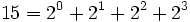 15 = 2^0 + 2^1 + 2^2 + 2^3\, les exposants formant un ensemble fini.
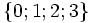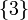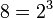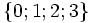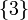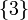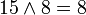
Donc pour 15 l'ensemble est: \left\{ 0; 1; 2; 3 \right\} et pour 8 l'ensemble est: \left\{ 3 \right\} (8 = 2^3\,), donc l'intersection entre l'ensemble \left\{ 0; 1; 2; 3 \right\} et \left\{ 3 \right\} est \left\{ 3 \right\}. donc 15 \wedge 8 = 8

Propriétés

pour tout a,b et n entier on a:

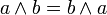
  1. a \wedge b = b \wedge a
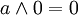
  2. a \wedge 0 = 0
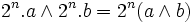
  3. 2^n.a \wedge 2^n.b =2^n(a \wedge b)
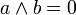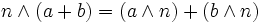
  4. si a \wedge b = 0 alors n \wedge (a+b) =(a \wedge n)+(b \wedge n)
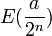  5. si E(\frac{a}{2^n}) est pair, alors on a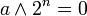 a \wedge 2^n = 0
  6. si 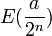E(\frac{a}{2^n}) est impair, alors on a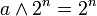 a \wedge 2^n = 2^n
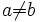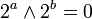
  7. si a \not= b on a 2^a \wedge 2^b=0

Opération la disjonction (ou) sur les bits

La disjonction entre deux entiers, est un entier associé à un ensemble qui est l'union des deux ensembles qui sont associés à ces deux nombres.
La disjonction (ou) entre deux entiers a et b, se représente: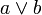a \vee b.
exemple:
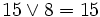
15 \vee 8 = 15

Propriétés

pour tout a,b et n entier on a:

  1. a \vee b = b \vee a
  2. a \vee 0 = a
  3. 2^n.a \vee 2^n.b =2^n(a \vee b)

Opérations sur les bits dans \mathbb{Z}

La négation

Définition

La négation d'un entiers relatif est:
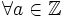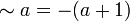
\forall a \in \mathbb{Z} on a \sim a=-(a+1)

conjonction et disjonction dans \mathbb{Z}

Pour calculer les opérations conjonction et disjonction, on utilise les proriétés suivantes

Propriétés

pour tout a,b et n entiers relatifs on a:

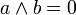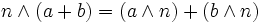
  1. si a \wedge b = 0 alors n \wedge (a+b) =(a \wedge n)+(b \wedge n)
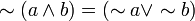  2. \sim (a \wedge b) = ( \sim a \vee \sim b) (De Morgan)
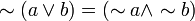  3. \sim (a \vee b) = ( \sim a \wedge \sim b) (De Morgan)
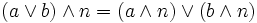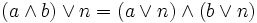
  4. (a \vee b) \wedge n = (a \wedge n) \vee (b \wedge n) et (a \wedge b) \vee n = (a \vee n) \wedge (b \vee n)

conjonction et disjonction dans \mathbb{Q}

La division euclidienne dans le système binaire

Pour tous couple, a et b dans 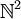\mathbb{N}^2 il existe un seul couple dans 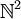\mathbb{N}^2. c'est vrai dans tous les systèmes.
Donc on peut faire une division sur le système binaire, si r est le reste d'une division, multiplier r par 10 est en fait la division:
exemple: La division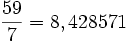 {59 \over 7} =8,428571,
est en système décimal, pour le système binaire, on fait les mêmes opérations, et on trouve:
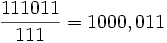{111011 \over 111} =1000,011, donc on peut faire les opérations conjonction et disjonction pour les nombres rationnels.

Ce document provient de « Op%C3%A9rations sur les bits ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Operations sur les bits de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Opérations sur les bits — Sommaire 1 Introduction 2 Opération conjonction (et) sur les bits 2.1 Présenter les entiers dans les ensembles fini 2.2 Propriétés …   Wikipédia en Français

  • Cryptographie Sur Les Courbes Elliptiques — En cryptographie, les courbes elliptiques, des objets mathématiques, peuvent être utilisées pour des opérations asymétriques comme des échanges de clés sur un canal non sécurisé ou un chiffrement asymétrique, on parle alors de cryptographie sur… …   Wikipédia en Français

  • Cryptographie sur les courbes elliptiques — En cryptographie, les courbes elliptiques, des objets mathématiques, peuvent être utilisées pour des opérations asymétriques comme des échanges de clés sur un canal non sécurisé ou un chiffrement asymétrique, on parle alors de cryptographie sur… …   Wikipédia en Français

  • Cryptologie sur les courbes elliptiques — Cryptographie sur les courbes elliptiques En cryptographie, les courbes elliptiques, des objets mathématiques, peuvent être utilisées pour des opérations asymétriques comme des échanges de clés sur un canal non sécurisé ou un chiffrement… …   Wikipédia en Français

  • Les plates-formes C2 — Liaison 16 La Liaison 16 (L16) est un standard de liaison de donnée de l OTAN pour l échange d informations tactiques entre des unités militaires. Elle est définie par le STANAG 5516. Sa mise en œuvre opérationnelle est définie dans le document… …   Wikipédia en Français

  • Les plates-formes Non-C2 — Liaison 16 La Liaison 16 (L16) est un standard de liaison de donnée de l OTAN pour l échange d informations tactiques entre des unités militaires. Elle est définie par le STANAG 5516. Sa mise en œuvre opérationnelle est définie dans le document… …   Wikipédia en Français

  • Floating-Point Operations Per Second — (FLOPS) (opérations à virgule flottante par seconde) est une mesure commune de repère pour évaluer la vitesse des microprocesseurs. Les opérations en virgule flottante incluent toutes les opérations qui impliquent des nombres réels. De telles… …   Wikipédia en Français

  • Floating-point operations per second — (FLOPS) (opérations à virgule flottante par seconde) est une mesure commune de repère pour évaluer la vitesse des microprocesseurs. Les opérations en virgule flottante incluent toutes les opérations qui impliquent des nombres réels. De telles… …   Wikipédia en Français

  • Compter sur ses doigts — Les doigts sont couramment utilisés, notamment par les enfants, pour apprendre à compter. Selon les pays et les coutumes, on compte différemment sur ses doigts : en occident, on compte généralement jusqu à 10 en utilisant les deux mains. En… …   Wikipédia en Français

  • Compter Sur Ses Doigts — Les doigts sont couramment utilisés, notamment par les enfants, pour apprendre à compter. Selon les pays et les coutumes, on compte différemment sur ses doigts : en occident, on compte généralement jusqu à 10 en utilisant les deux mains. En… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”