- Algèbre élémentaire
-
Algèbre élémentaire
L'algèbre élémentaire est une branche des mathématiques dont l'objet est l'étude des lois qui régissent les quantités numériques. Le qualificatif d'élémentaire apparaît en même temps que l'algèbre moderne afin de la différencier de celle-ci. Aujourd'hui, c'est la première approche de l'algèbre dans le cursus scolaire.
L'algèbre se différencie de l'arithmétique par l'introduction de lettres (a, b, c, ..., x, y, z, ..., α, β, γ, ...) représentant indifféremment tous les nombres et auxquelles sont appliquées les mêmes règles de calculs que s'il s'agissait de nombres.
Il est ainsi possible d'établir des lois ne dépendant que de la nature des opérations, indépendamment des nombres.
La résolutions d'équations et d'inéquations, l'étude des polynômes sont des applications de l'algèbre.
Sommaire
Expressions algébriques
Une expression algébrique est constituée de nombres, de lettres et de signes opératoires :
- le signe + est utilisé pour marquer l'addition.
- le signe − est utilisé pour marquer la soustraction.
- les signes
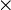ou 
sont utilisés pour marquer la multiplication. Quand la multiplication concerne deux lettres, il est possible d'écrire ab au lieu de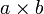 
. - le signe
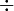est utilisé pour marquer la division, 
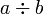pouvant également s'écrire 
.
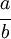Par exemple :
- Le produit d'un nombre x augmenté de 3 par lui-même s'écrit (x + 3)x.
- La différence des carrés de deux nombres a et b s'écrit a2 − b2
Évaluer une expression algébrique consiste à attribuer une valeur à chacune des variables, puis à effectuer le calcul arithmétique obtenu.
Par exemple évaluer l'expression x2 + x − 1 pour x = 2 consiste à effectuer le calcul 22 + 2 − 1.
Propriétés de l'addition
-
- est écrit a + b;
- est commutative: a + b = b + a;
- est associative: (a + b) + c = a + (b + c);
- a une application réciproque appelée subtraction: (a + b) − b = a, équivaut à additionner un nombre négatif, a − b = a + (−b);
- a un élément neutre 0 qui conserve le nombre: a + 0 = a.
Propriétés de la multiplication
-
- est écrit a × b or a • b;
- est commutative: a × b = b × a;
- est associative: (a × b) × c = a × (b × c);
- est abbrevié par la juxtaposition: a × b ≡ ab;
- a un élément neutre 1 qui conserve le nombre: a × 1 = a;
- pour les numbre différent de zero, a une application réciproque appelée division: (ab)/b = a, équivaut à multiplier par son inverse, a/b = a(1/b);
- est distributive par rapport à l'addition: (a + b)c = ac + bc;
Factorisation et développement
Factoriser une expression algébrique, E, consiste à en transformer l'écriture sous la forme d'un produit de deux ou plusieurs expressions (A, B, ...) :
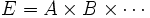
Chacune des expressions A, B, ... est appelée un facteur.
Développer une expression algébrique, E, consiste à en transformer l'écriture sous la forme d'une somme (ou différence) de deux ou plusieurs expressions. (A, B, ...) :
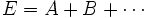
Chacune des expressions A, B, ... est appelée un terme.
Voir aussi
Catégorie : Algèbre
Wikimedia Foundation. 2010.
