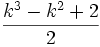Nombre Polygonal Centré

Nombre Polygonal Centré

Nombre polygonal centré

Un nombre polygonal centré est un type de nombre figuré, qui peut être représenté par une figure plane ayant un point placé en son centre et tous les autres points disposés autour de ce centre formant des couches polygonales successives avec un nombre constant de côtés. Chaque côté d'un polygone d'une couche contient au moins un point de plus que n'importe quel côté du polygone de la couche précédente. Ainsi, dans une figure représentant un nombre k-gonal centré, à partir de la deuxième couche polygonale, chaque couche contient au moins k points de plus que la couche précédente.

Des exemples de nombres centrés sont

Chaque suite de nombres centrés peut être formée en additionnant 1 à un multiple fixe d'un précédent nombre triangulaire, et donc algébriquement, le nombre k-gonal centré de rang nest égal à

Ckn = kTn − 1 + 1

où T est un nombre triangulaire.

Exactement comme dans le cas des nombres polygonaux réguliers, le premier nombre k-gonal est 1. Ainsi, pour tout entier k strictement positif, 1 est un nombre k-gonal et aussi un nombre k-gonal centré. Le nombre suivant à être à la fois k-gonal et k-gonal centré est égal à

{k^3-k^2+2}\over2

Ce qui permet de voir que 10 est triangulaire et triangulaire et centré, 25 est à la fois un nombre carré et carré centré, etc.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre polygonal centr%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Polygonal Centré de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Nombre polygonal centre — Nombre polygonal centré Un nombre polygonal centré est un type de nombre figuré, qui peut être représenté par une figure plane ayant un point placé en son centre et tous les autres points disposés autour de ce centre formant des couches… …   Wikipédia en Français

  • Nombre polygonal centré — Un nombre polygonal centré est un type de nombre figuré, qui peut être représenté par une figure plane ayant un point placé en son centre et tous les autres points disposés autour de ce centre formant des couches polygonales successives avec un… …   Wikipédia en Français

  • Nombre Centré — En mathématiques, les nombres centrés sont une classe des suites de nombres figurés, chacun formés par un point central, entouré par des couches polygonales successives constituées d un nombre constant de côtés. Chaque côté d une couche… …   Wikipédia en Français

  • Nombre centre — Nombre centré En mathématiques, les nombres centrés sont une classe des suites de nombres figurés, chacun formés par un point central, entouré par des couches polygonales successives constituées d un nombre constant de côtés. Chaque côté d une… …   Wikipédia en Français

  • Nombre Triangulaire — Un nombre triangulaire est un nombre qui peut être représenté par un triangle équilatéral. Les premiers termes de la suite des nombres triangulaires (A000217 dans l encyclopédie électronique des suites entières) sont: 0, 1, 3, 6, 10, 15, 21, 28,… …   Wikipédia en Français

  • Nombre centré — En mathématiques, les nombres centrés sont une classe des suites de nombres figurés, chacun formés par un point central, entouré par des couches polygonales successives constituées d un nombre constant de côtés. Chaque côté d une couche… …   Wikipédia en Français

  • Nombre Carré — Carré parfait En mathématiques, un entier n est un carré parfait (un carré s il n y a pas ambiguïté) s il existe un entier k tel que n = k2 ; en d autres termes, un carré parfait est le carré d un entier. Par exemple, les entiers 0, 1, 4 ou… …   Wikipédia en Français

  • Nombre carre — Carré parfait En mathématiques, un entier n est un carré parfait (un carré s il n y a pas ambiguïté) s il existe un entier k tel que n = k2 ; en d autres termes, un carré parfait est le carré d un entier. Par exemple, les entiers 0, 1, 4 ou… …   Wikipédia en Français

  • Nombre carré — Carré parfait En mathématiques, un entier n est un carré parfait (un carré s il n y a pas ambiguïté) s il existe un entier k tel que n = k2 ; en d autres termes, un carré parfait est le carré d un entier. Par exemple, les entiers 0, 1, 4 ou… …   Wikipédia en Français

  • Nombre triangulaire — Cette figure illustre le fait de 28 est le septième nombre triangulaire. En arithmétique, un nombre triangulaire est un cas particulier de nombre figuré. Il correspond à un nombre entier positif égal au nombre de pastilles dans un triangle… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”