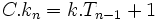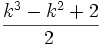Nombre Centré

Nombre Centré

Nombre centré

En mathématiques, les nombres centrés sont une classe des suites de nombres figurés, chacun formés par un point central, entouré par des couches polygonales successives constituées d'un nombre constant de côtés.

Chaque côté d'une couche polygonale contient un point en plus que le côté de la couche précédente, ainsi, en démarrant de la seconde couche polygonale chaque couche d'un nombre k-gonal centré contient k points en plus que la couche précédente.

Ces suites sont les suivantes :

Chaque suite peut être formée en ajoutant 1 à un multiple fixé au nombre triangulaire précédent, ou exprimé algébriquement, le n ième nombre k-gonal centré est obtenu par la formule

C.k_n = k.T_{n-1}+1\,

où T est un nombre triangulaire.

De la même façon avec les nombres polygonaux réguliers, le premier nombre k-gonal centré est 1. Ainsi, pour tout k, 1 est, et un nombre k-gonal, et un nombre k-gonal centré. Le nombre suivant étant à la fois k-gonal et k-gonal centré peut être trouvé en utilisant la formule

{k^3-k^2+2}\over2\,

qui nous indique que 10 est à la fois triangulaire et triangulaire centré, 25 est à la fois carré et carré centré, etc.

Bien qu'un nombre premier p ne puisse pas être un nombre polygonal régulier (excepté, bien sûr, le deuxième nombre k-gonal), les nombres premiers apparaissent "assez souvent" dans les suites de nombres polygonaux centrés.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre centr%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Centré de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Nombre centre — Nombre centré En mathématiques, les nombres centrés sont une classe des suites de nombres figurés, chacun formés par un point central, entouré par des couches polygonales successives constituées d un nombre constant de côtés. Chaque côté d une… …   Wikipédia en Français

  • Nombre centré — En mathématiques, les nombres centrés sont une classe des suites de nombres figurés, chacun formés par un point central, entouré par des couches polygonales successives constituées d un nombre constant de côtés. Chaque côté d une couche… …   Wikipédia en Français

  • Nombre D'or —  Pour l’article homonyme, voir Nombre d or (astronomie).  La proportion définie par a et b est dite d extrême et de moyenne raison lorsque a e …   Wikipédia en Français

  • Nombre d'Or —  Pour l’article homonyme, voir Nombre d or (astronomie).  La proportion définie par a et b est dite d extrême et de moyenne raison lorsque a e …   Wikipédia en Français

  • Nombre d’or — Nombre d or  Pour l’article homonyme, voir Nombre d or (astronomie).  La proportion définie par a et b est dite d extrême et de moyenne raison lorsque a e …   Wikipédia en Français

  • Centre D'accueil De Demandeurs D'asile — en France Pour les articles homonymes, voir CADA …   Wikipédia en Français

  • Centre d'accueil de demandeurs d'asile — en France Pour les articles homonymes, voir CADA …   Wikipédia en Français

  • Nombre Constructible — Un nombre constructible à la règle et au compas est la mesure d une longueur associée à deux points constructibles à la règle et au compas. Ainsi, est un nombre constructible, mais ni ni π ne le sont. C est du moins ainsi que le définissaient les …   Wikipédia en Français

  • Nombre constructible à la règle — Nombre constructible Un nombre constructible à la règle et au compas est la mesure d une longueur associée à deux points constructibles à la règle et au compas. Ainsi, est un nombre constructible, mais ni ni π ne le sont. C est du moins ainsi que …   Wikipédia en Français

  • Nombre constructible à la règle et au compas — Nombre constructible Un nombre constructible à la règle et au compas est la mesure d une longueur associée à deux points constructibles à la règle et au compas. Ainsi, est un nombre constructible, mais ni ni π ne le sont. C est du moins ainsi que …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”