- Maximum local
-
Extremum

« Maximum » et « Minimum » redirigent ici. Pour les autres significations, voir Maximum (homonymie) et Minimum (homonymie). L'expression « élément extremum » signifie « élément maximum » ou « élément minimum ».
Dans un ensemble ordonné, le plus grand élément (resp. plus petit élément) ou élément maximum (resp. élément minimum) d'une partie de cet ensemble est l'élément qui, quand il existe, appartient à cette partie et est supérieur (resp. inférieur) à tous autres éléments de la partie.
Sommaire
Propriétés
Le plus grand (resp. plus petit) élément d'une partie est donc en particulier :
- un élément maximal (resp. élément minimal) de la partie
- un majorant (resp. minorant) de la partie
- la borne supérieure (resp. borne inférieure) de la partie
... mais les réciproques sont fausses. On peut néanmoins énoncer les théorèmes suivants :
- Si une partie admet un plus grand élément (resp. plus petit élément), alors il n'y a qu'un seul élément maximal (resp. minimal) et c'est le plus grand élément (resp. plus petit élément) de la partie.
- Si une partie admet un majorant (resp. minorant) qui appartient à cette partie, alors la partie admet un plus grand élément (resp. plus petit élément) qui est précisément ce majorant (resp. minorant).
Exemple
- Prenons pour ensemble ordonné E l'ensemble des intervalles réels ordonnés par la relation d'inclusion.
- Choisissons comme partie P à étudier, l'ensemble des intervalles inclus dans
![[-1; 0 [\cup]0 ; 1]](/pictures/frwiki/101/e808687072e4483e028d29b989f948cf.png) .
. - Tout élément de P inclut l'ensemble vide, donc l'ensemble vide est un minorant de P. Or l'ensemble vide est élément de P, c'est donc aussi sa borne inférieure et son plus petit élément.
- Tout élément de P est inclus dans l'intervalle [-1 ; 1] qui est élément de E mais pas de P. Donc [-1 ; 1] est un majorant de P, mais pas son plus grand élément. Malgré tout, c'est son plus petit majorant, donc sa borne supérieure.
- Il n'existe aucun élément de P qui soit supérieur à ]0 ; 1]. ]0 ; 1] est donc un élément maximal de P. Mais il existe des éléments de P qui ne lui sont pas comparables, par exemple [1/2 ; 3/2]. Donc ]0 ; 1] n'est pas le plus grand élément de P. Et pour cause, il existe un autre élément maximal distinct : [-1 ; 0[, donc P n'a pas de plus grand élément !
Extremum d'une fonction
Soient ( F, ≤ ) un ensemble totalement ordonné et f une fonction de l'ensemble E vers l'ensemble F.
Notons D, l'ensemble de définition de f et soit a un élément quelconque de D.
On rappelle que si A est une partie de D ou D lui-même, alors la notation f(A) désigne l'image de A par la fonction f.
Extremum global d'une fonction
Un « extremum global de f » est un « maximum global de f » ou un « minimum global de f ».
Maximum global
On dit que f(a) est le « maximum » ou le « maximum global » de f si et seulement si pour tout élément x de D, on a f(x) ≤ f(a).
Cela équivaut à dire que f(a) est le plus grand élément de f(D).
Minimum global
On dit que f(a) est le « minimum » ou le « minimum global » de f si et seulement si pour tout élément x de D, on a f(a) ≤ f(x).
Cela équivaut à dire que f(a) est le plus petit élément de f(D).
Extremum local d'une fonction
La notion d'extremum local suppose définie sur D une structure topologique (donnant un sens précis à l'adjectif local). Dès lors, un « extremum local de f sur D » est un « maximum local de f sur D » ou un « minimum local de f sur D ».
Maximum local
Soit D un espace topologique. Étant donné un point a de D, on dit que f atteint en a un maximum local s'il existe un voisinage V de a tel que pour tout élément x de V, on ait f(a) ≥ f(x).
On dit alors que f(a) est un « maximum local » de f sur D.Minimum local
Soit D un espace topologique. Étant donné un point a de D, on dit que f atteint en a un minimum local s'il existe un voisinage V de a tel que pour tout élément x de V, on ait f(a) ≤ f(x).
On dit alors que f(a) est un « minimum local » de f sur D.Méthodes usuelles de recherche des extremums d'une fonction
La notion d'extremum d'une fonction est surtout intéressante en analyse lorsque l'ensemble d'arrivée F est l'ensemble totalement ordonné
 des nombres réels. Dans ce cas, le calcul différentiel est un moyen efficace de recherche des extremums locaux.
des nombres réels. Dans ce cas, le calcul différentiel est un moyen efficace de recherche des extremums locaux.On cite ici quelques méthodes essentielles, en se limitant aux fonctions à valeurs réelles d'une ou plusieurs variables réelles.
Cas des fonctions réelles d'une variable réelle
Soit une fonction
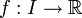 , où I est un intervalle de
, où I est un intervalle de  non réduit à un point. Un point est intérieur à I si et seulement si c'est un élément de I qui n'est pas une borne de l'intervalle.
non réduit à un point. Un point est intérieur à I si et seulement si c'est un élément de I qui n'est pas une borne de l'intervalle.- Existence d'extremums globaux (théorème des bornes) :
- si I est fermé borné et si f est continue, alors f admet sur I un maximum global et un minimum global.
- Condition nécessaire pour un extremum local :
- si f atteint un extremum local en un point a intérieur à I et si elle est dérivable en ce point, alors
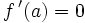 .
.
Pour cette raison, l'étude des extremums passe souvent par la recherche des points d'annulation de la dérivée, appelés points critiques de f. Un point critique n'est pas nécessairement un extremum, comme le montre l'exemple de la fonction
au point 0. On peut, cependant, sous certaines hypothèses supplémentaires, affirmer qu'un point critique est un extremum.
- Condition suffisante pour un extremum local :
- Si f est dérivable sur I, et si a est un point intérieur à I où la dérivée de f s'annule en changeant de signe, alors f atteint un extremum local en a. Plus précisément, en supposant
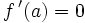 :
:
- S'il existe α réel strictement positif tel que
![[a-\alpha,\, a + \alpha] \subset I](/pictures/frwiki/101/e651416c3f9e32be2dbb726e139ac207.png)
- et
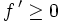 sur
sur ![[a-\alpha,\, a]](/pictures/frwiki/57/90b20f5f95833dbdd9f2cf09e194d37e.png) ,
, 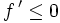 sur
sur ![[a,\, a + \alpha]](/pictures/frwiki/55/7d2fb273c68d8938e6a1f00353232942.png) ,
, - alors f atteint un maximum local en a.
- S'il existe α réel strictement positif tel que
![[a-\alpha,\, a + \alpha] \subset I](/pictures/frwiki/101/e651416c3f9e32be2dbb726e139ac207.png)
- et
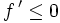 sur
sur ![[a-\alpha,\, a]](/pictures/frwiki/57/90b20f5f95833dbdd9f2cf09e194d37e.png) ,
, 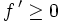 sur
sur ![[a,\, a + \alpha]](/pictures/frwiki/55/7d2fb273c68d8938e6a1f00353232942.png) ,
, - alors f atteint un minimum local en a.
- S'il existe α réel strictement positif tel que
- Remarque
La condition nécessaire pour un extremum local ne s'applique pas aux bornes de l'intervalle. Par exemple, la fonction
admet deux extremums globaux (a fortiori locaux), atteints en 0 et 1. Par ailleurs, elle est dérivable et sa dérivée ne s'annule en aucun point.
Cas des fonctions réelles de plusieurs variables réelles
Soit une fonction
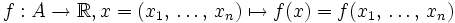 , où A est une partie non vide de
, où A est une partie non vide de 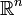 .
.- Existence d'extremums globaux (théorème des bornes) :
- si A est fermé borné et si f est continue, alors f admet sur A un maximum global et un minimum global.
- Condition nécessaire pour un extremum local :
- On suppose ici que A est un ouvert, et que f est de classe C1 sur A.
- Si f atteint un extremum local en un point a de A, alors
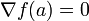 : le gradient de f en ce point est nul.
: le gradient de f en ce point est nul. - Rappel : par définition, le gradient de f en a est le vecteur de
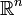 :
: 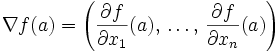 .
.
Les points d'annulation du gradient portent le nom de points critiques de la fonction f.
- Condition suffisante pour un extremum local :
- On suppose ici que A est un ouvert, et que f est de classe C2 sur A.
- On considère un point a de A. La (matrice) hessienne de f en a est notée
 ; elle est symétrique réelle.
; elle est symétrique réelle.
- Si
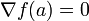 et si
et si  est définie négative, alors f atteint un maximum local en a.
est définie négative, alors f atteint un maximum local en a. - Si
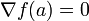 et si
et si  est définie positive, alors f atteint un minimum local en a.
est définie positive, alors f atteint un minimum local en a.
- Si
- Rappel : par définition, la hessienne de f en a est la matrice carrée d'ordre n ayant
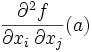 pour élément en ligne i et colonne j.
pour élément en ligne i et colonne j. - Comme f est de classe C2, il résulte du théorème de Schwarz sur les dérivées partielles d'ordre 2 que la hessienne est symétrique.
Fonction optimum de deux fonctions
Les fonctions minimum et maximum de deux fonctions peuvent être définies à l'aides de valeurs absolues :
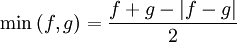

- Portail des mathématiques
Catégories : Analyse | Théorie des ordres
Wikimedia Foundation. 2010.

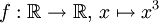
![f : [0, 1] \to\R,\, x \mapsto x](/pictures/frwiki/50/2d14b4188b88ac9a63a7f7025ba45bec.png)
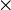


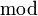

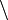
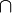

 Produit en couronne
Produit en couronne
 Somme connexe
Somme connexe

 Cup produit
Cup produit