Localement (topologie)
- Localement (topologie)
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Localement (topologie) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
TOPOLOGIE - Topologie algébrique — Inventée au début du XXe siècle pour résoudre des problèmes géométriques, la topologie algébrique connut un grand développement grâce à l’introduction de constructions algébriques de plus en plus abstraites. Pour clarifier l’exposé, on a… … Encyclopédie Universelle
TOPOLOGIE - Topologie générale — Les notions de continuité et de limite ont une origine intuitive et l’on se propose d’analyser ici cette intuition. Considérons, par exemple, la description de la tangente T à une courbe (fig. 1) telle qu’on la trouve dans les manuels classiques… … Encyclopédie Universelle
TOPOLOGIE - Topologie différentielle — La topologie différentielle, que l’on devrait plutôt appeler «topologie des variétés », est une discipline mathématique assez ancienne par les problèmes qu’elle cherche à résoudre: ils étaient presque tous posés au début du siècle; mais ses… … Encyclopédie Universelle
Topologie grossiere — Topologie grossière En mathématiques, la topologie grossière (ou topologie triviale) associée à un ensemble est une topologie où les seuls ouverts sont l ensemble vide et l espace lui même. Cette topologie est la moins fine de toutes les… … Wikipédia en Français
Topologie triviale — Topologie grossière En mathématiques, la topologie grossière (ou topologie triviale) associée à un ensemble est une topologie où les seuls ouverts sont l ensemble vide et l espace lui même. Cette topologie est la moins fine de toutes les… … Wikipédia en Français
Topologie de zariski — En géométrie algébrique, le terme topologie de Zariski peut désigner trois notions proches: une certaine topologie définie sur une variété algébrique une topologie définie de manière analogue sur le spectre premier d un anneau commutatif une… … Wikipédia en Français
Topologie d'un espace vectoriel de dimension finie — En mathématiques, la topologie d un espace vectoriel de dimension finie sur un corps K est, sous certaines hypothèses, un cas particulier de topologie d espace vectoriel normé. Le prototype est Rn muni de la norme qui à un n uplet de réels… … Wikipédia en Français
Topologie quotient — En mathématiques, la topologie quotient consiste intuitivement à créer une topologie en collant certains points d un espace donné sur d autres, par le biais d une relation d équivalence bien choisie. Cela est souvent fait dans le but de… … Wikipédia en Français
Topologie compacte-ouverte — En mathématiques, la topologie compacte ouverte est une topologie définie sur l ensemble des applications continues entre deux espaces topologiques. C est l une des topologies les plus utilisées sur un tel espace fonctionnel, et elle est employée … Wikipédia en Français
Topologie faible — En mathématiques, la topologie faible d un espace vectoriel topologique E est une topologie définie sur E au moyen de son dual topologique E . On définit également sur E une topologie dite faible * au moyen de E. Sommaire 1 Topologie affaiblie d… … Wikipédia en Français
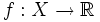 définie sur un espace topologique
définie sur un espace topologique 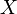 admet en en point
admet en en point 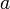 de
de 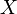 un maximum local s'il existe un voisinage
un maximum local s'il existe un voisinage 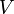 de
de 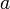 tel que
tel que 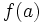 soit la plus grande valeur de
soit la plus grande valeur de 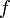 sur
sur 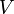 .
.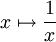 est localement non bornée au point
est localement non bornée au point 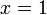 sous prétexte qu'elle est non bornée sur
sous prétexte qu'elle est non bornée sur ![\ ]0,2[](/pictures/frwiki/100/dedacbd3e00ecbfbe606bd1bad76424f.png) (qui est un voisinage du point considéré).
(qui est un voisinage du point considéré).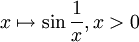 , dans
, dans 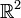 , et le point
, et le point 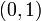 . Pourtant, l'espace tout entier est un voisinage connexe de ce point.
. Pourtant, l'espace tout entier est un voisinage connexe de ce point.