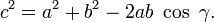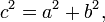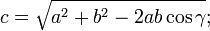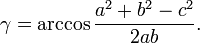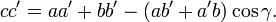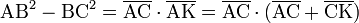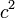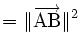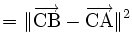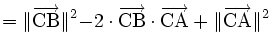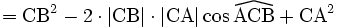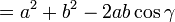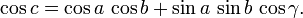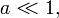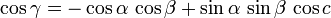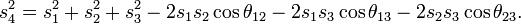Loi des cosinus

Théorème d'Al-Kashi

Fig. 1 - Notations usuelles dans un triangle quelconque.

Le théorème d'Al-Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d'autres langues, est un théorème de géométrie du triangle couramment utilisé en trigonométrie. Il généralise le théorème de Pythagore aux triangles non rectangles : il relie le troisième côté d'un triangle aux deux premiers ainsi qu'au cosinus de l'angle formé par ces deux côtés. Le nom français au mathématicien perse (Ghiyath al-Kashi), qui a vécu entre 1380 et 1429, lui a été attribué en France dans les années 1990, les appellations théorème de Pythagore généralisé ou loi des cosinus étant utilisées jusque là.

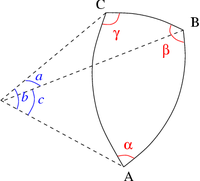
Soit un triangle ABC, dans lequel on utilise les notations usuelles exposées sur la figure 1 : d'une part α, β et γ pour les angles et, d'autre part, a, b et c pour les côtés respectivement opposés à ces angles. Alors, le théorème d'al-Kashi s'énonce de la façon suivante :

$c^2 = a^2 + b^2 - 2ab\ \cos\ \gamma.$

Sommaire

1 Histoire
2 Le théorème et ses applications
3 Démonstrations
4 Généralisation aux géométries non euclidiennes
- 4.1 Géométrie sphérique
- 4.2 Géométrie hyperbolique
5 Généralisation à l'espace euclidien
6 Voir aussi

Histoire

Fig. 2 - Triangle ABC avec hauteur BH

Les Éléments d'Euclide datant du III^e siècle av. J.-C., contenaient déjà une approche géométrique de la généralisation du théorème de Pythagore : les propositions 12 et 13 du livre II, traitent séparément le cas d'un triangle obtusangle et celui d'un triangle acutangle. La formulation de l'époque est pédestre car l'absence de fonction trigonométrique et d'algèbre oblige à raisonner en termes de différences d'aires. Aussi la proposition 12 utilise-t-elle ces termes :

«
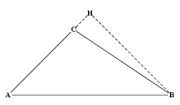
Dans les triangles obtusangles, le carré du côté qui soutient l'angle obtus est plus grand que la somme des carrés des deux autres côtés, de la quantité de deux fois le rectangle formé d'un des côtés contenant l'angle obtus, à savoir celui sur le prolongement duquel tombe la hauteur, et de la ligne prise en-dehors entre [le pied de] la hauteur et l'angle obtus.
»

— Euclide, Les Éléments

En notant ABC le triangle d'angle obtus A et H le pied de la hauteur issue de B (cf. Fig. 2 ci-contre), les notations modernes permettent de résumer l'énoncé ainsi :

AB² = CA² + CB² + 2 CA CH.

Il fallut attendre la trigonométrie arabo-musulmane au Moyen Âge pour voir le théorème évoluer dans sa forme et dans sa portée : l'astronome et mathématicien al-Battani généralisa le résultat d'Euclide à la géométrie sphérique au début du X^e siècle, ce qui permit d'effectuer des calculs de distance angulaire entre étoiles. C'est durant la même période que se sont établies les premières tables trigonométriques, pour les fonctions sinus et cosinus. Cela permit à Ghiyath al-Kashi, mathématicien de l'école de Samarcande, de mettre le théorème sous une forme utilisable pour la triangulation au cours du XV^e siècle. La propriété a été popularisée en occident par François Viète qui l'a, semble-t-il, redécouverte indépendamment.

C'est au début du XIX^e siècle que les notations algébriques modernes permettent d'écrire le théorème sous sa forme actuelle et qu'il prend dans de nombreuses langues le nom de loi (ou théorème) des cosinus.

Le théorème et ses applications

Le théorème d'Al-Kashi est également connu sous le nom de théorème de Pythagore généralisé, car le théorème de Pythagore en est un cas particulier : lorsque l'angle $γ$ est droit, autrement dit lorsque $cosγ = 0$ , le théorème d'Al-Kashi s'écrit

$c^2=a^2+b^2, \,$

et réciproquement.

Fig. 3 - Utilisation du théorème d'Al-Kashi : angle ou côté inconnu.

Le théorème s'utilise en triangulation (voir Fig. 3) pour résoudre un triangle, à savoir déterminer

le troisième côté d'un triangle dont on connaît un angle et les côtés adjacents :

$c = \sqrt{a^2+b^2-2ab\cos\gamma}; \,$

les angles d'un triangle dont on connaît les trois côtés :

$\gamma = \arccos \dfrac{a^2+b^2-c^2}{2ab}.$

Ces formules sont instables numériquement dans le cas de triangles en épingle, c'est-à-dire lorsque c est petit devant a et b — ou, de façon équivalente, lorsque γ est petit devant 1.

Il existe un corollaire du théorème d'al-Kashi : pour deux triangles directement semblables ABC et A'B'C'

$cc' = aa' + bb' - (ab'+a' b)\cos \gamma. \,$

Démonstrations

Par un découpage d'aires

Fig. 4a - Démonstration du théorème d'Al-Kashi pour les triangles à angles aigus : « méthode du découpage ».

Fig. 4b - Démonstration du théorème d'Al-Kashi dans le cas d'un angle obtus : « méthode du découpage »

Un certain nombre des démonstrations du théorème font intervenir un calcul d'aires. Il convient en effet de remarquer que

$a 2$ , $b 2$ et $c 2$ sont les aires de carrés de côtés respectifs $a$ , $b$ et $c$ ;
$a b | cosγ |$ est celle d'un parallélogramme de côtés $a$ et $b$ formant un angle $π / 2 - γ$ , le changement de signe de $cosγ$ lorsque l'angle $γ$ devient obtus rendant une étude par cas obligatoire.

La figure 4a (ci-contre) découpe un heptagone de deux manières différentes de sorte à démontrer le théorème d'Al-Kashi dans le cas d'un angle aigu. Interviennent :

en rose, les aires $a 2$ , $b 2$ à gauche, et les aires $2 a b cosγ$ et $c 2$ à droite ;
en bleu, le triangle ABC, à droite comme à gauche ;
en gris, quelques triangles supplémentaires, identiques au triangle ABC et en même nombre dans les deux découpages.

L'égalité des aires de droite et de gauche donne

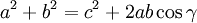$\,a^2+b^2 = c^2+2ab \cos\gamma$ .

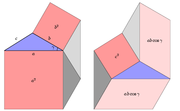
La figure 4b (ci-contre) découpe un hexagone de deux manières différentes de sorte à faire démontrer le théorème d'al-Kashi dans le cas d'un angle obtus. La figure montre

en rose, les aires $a 2$ , $b 2$ et $- 2 a b cosγ$ à gauche, et l'aire $c 2$ à droite ;
en bleu, deux fois le triangle ABC, à droite comme à gauche.

L'égalité des aires à droite et à gauche donne

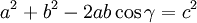$\,a^2+b^2-2ab\cos\gamma = c^2$ .

Une démonstration rigoureuse nécessiterait de prouver que les deux découpages sont effectivement identiques, ce qui utilise principalement les cas d'égalité des triangles.

Par le théorème de Pythagore

Fig. 5 - Démonstration du théorème d'Al-Kashi en utilisant les relations trigonométriques

La figure 5 (ci-contre) indique la manière de procéder pour démontrer le théorème d'Al-Kashi dans le cas d'un triangle à angles aigus en utilisant le théorème de Pythagore sur un sous-triangle rectangle formé en prenant le pied de la hauteur. Seule la dernière étape n'est pas indiquée sur la figure : le théorème de Pythagore s'applique au triangle rectangle dont le côté c est l'hypoténuse :

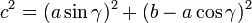$\,c^2 = (a\sin\gamma)^2 + (b-a\cos\gamma)^2$ ,

ce qui donne le résultat escompté, après simplification.

La méthode est en tous points similaire pour les angles obtus.

Par la Puissance d'un point par rapport à un cercle

Fig. 6 - Démonstration du théorème d'al-Kashi en utilisant la puissance d'un point par rapport à un cercle.

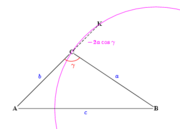
On considère le cercle de centre B et de rayon [BC] (cf. figure ci-contre). Il coupe la droite (AC) en C et K. La puissance du point A par rapport au dit cercle est

$\mathrm{AB}^2 - \mathrm{BC}^2 = \overline{\mathrm{AC}}\cdot\overline{\mathrm{AK}} = \overline{\mathrm{AC}}\cdot(\overline{\mathrm{AC}}+\overline{\mathrm{CK}})$

d'où

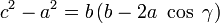$c^2-a^2 = b\,(b-2a\ \cos\ \gamma)$ .

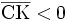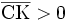Contrairement aux précédentes, pour cette démonstration, il n'est pas nécessaire de recourir à une étude par cas. En effet, les mesures algébriques permettent de traiter pareillement un angle aigu ( $\overline{\mathrm{CK}} < 0$ ) et un angle obtus ( $\overline{\mathrm{CK}} > 0$ ).

Par le calcul vectoriel

En utilisant le calcul vectoriel, plus précisément le produit scalaire, il est possible de retrouver le théorème d'Al-Kashi en quelques lignes :

$c^2\,$	$=\lVert\overrightarrow{\mathrm{AB}}\lVert^2$
	$= \lVert\overrightarrow{\mathrm{CB}}-\overrightarrow{\mathrm{CA}}\lVert^2$
	$=\lVert\overrightarrow{\mathrm{CB}}\lVert^2-2\cdot\overrightarrow{\mathrm{CB}}\cdot\overrightarrow{\mathrm{CA}}+\lVert\overrightarrow{\mathrm{CA}}\lVert^2$
	$=\mathrm{CB}^2-2\cdot\left\|\mathrm{CB}\right\|\cdot\left\|\mathrm{CA}\right\|\cos\widehat{\mathrm{ACB}}+\mathrm{CA}^2$
	$=a^2+b^2-2ab \cos\gamma\,$

Généralisation aux géométries non euclidiennes

Fig. 7 - Triangle sphérique : dimensions réduites a, b et c ; angles α, β et γ.

Pour une surface non euclidienne de courbure K, on note R le rayon de courbure. Il vérifie

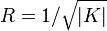$\,R = 1/\sqrt{|K|}$ .

On définit alors les dimensions réduites du triangle :

$\,a = BC/R$ ,

$\,b = AC/R$ ,

$\,c = AB/R$ .

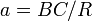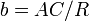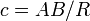Dans le cas d'un triangle sphérique, a, b et c correspondent à la mesure angulaire des segments de grand arc [BC], [AC] et [AB] (voir Fig. 7).

Géométrie sphérique

Dans un triangle sphérique ABC (Fig. 7), le théorème d'Al-Kashi s'écrit

$\cos c = \cos a \, \cos b + \sin a \, \sin b \, \cos\gamma.$

Lorsque le rayon de courbure est très grand devant les dimensions du triangle, c’est-à-dire lorsque

$\,a <\!\!< 1,$

etc. Cette expression se simplifie pour donner la version euclidienne du théorème d'Al-Kashi. Pour ce faire, on utilise les développements limités suivants :

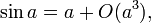$\,\sin a = a + O(a^3),$ etc.,

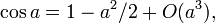$\,\cos a = 1 - a^2/2 + O(a^3),$ etc.

Il existe une identité similaire qui relie les trois angles :

$\cos\gamma = - \cos\alpha\,\cos\beta + \sin\alpha\,\sin\beta\,\cos c$

Géométrie hyperbolique

Dans un triangle hyperbolique ABC, le théorème d'al-Kashi s'écrit

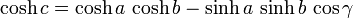$\cosh c = \cosh a\,\cosh b - \sinh a\,\sinh b\,\cos\gamma$ .

Lorsque le rayon de courbure devient très grand devant les dimensions du triangle, on retrouve le théorème d'al-Kashi euclidien à partir des développements limités

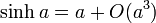$\,\sinh a = a + O(a^3)$ , etc.,

$\,\cosh a = 1 + a^2/2 + O(a^3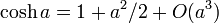)$ , etc.

Généralisation à l'espace euclidien

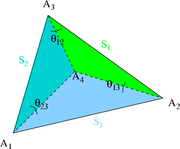
Fig. 8 - Tétraèdre : faces et angles diédraux.

On considère un tétraèdre A₁A₂A₃A₄ de l'espace euclidien. La figure 8 ci-contre présente les notations concernant les sommets, faces et angles dans le tétraèdre :

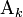$S k$ la face opposée au sommet $\mathrm A_k\$ ;
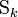$s k$ la surface de $\mathrm S_k\$ ;
$Δ k$ le plan dans lequel 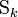$\mathrm S_k\$ est plongée ;
$θ i j$ l'angle diédral $(Δ i,Δ j)$ .

Alors, surfaces et angles vérifient :

$s_4^2 = s_1^2+s_2^2+s_3^2 - 2s_1s_2\cos\theta_{12} - 2s_1s_3\cos\theta_{13} - 2s_2s_3\cos\theta_{23}.\,$

Voir aussi

Liens externes

Ces liens ont servi de sources de l'article

Les Éléments, tome II, Euclide, sur la Bibliothèque nationale française en ligne.
Law of cosines, sur le site Math World (en anglais)

Bibliographie

Géométrie Supérieure, N. Éfimov, Moscou, Éditions MIR, 1981
Petite Encyclopédie des Mathématiques, Paris, Éditions K. Pagoulatos, 1980

La version du 14 février 2005 de cet article a été reconnue comme « article de qualité » (comparer avec la version actuelle).
Pour toute information complémentaire, consulter sa page de discussion et le vote l’ayant promu.

Portail de la géométrie

Ce document provient de « Th%C3%A9or%C3%A8me d%27Al-Kashi ».

Catégories : Article de qualité | Géométrie du triangle | Mathématiques élémentaires | Trigonométrie | Théorème de géométrie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi des cosinus de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Cosinus — Fonction trigonométrique Pour les articles homonymes, voir Cosinus (homonymie), Tangente et Sinus. Toutes les valeurs des fonctions trigonométriques en u … Wikipédia en Français
cosinus — [ kɔsinys ] n. m. • co sinus 1717; de co et sinus ♦ Fonction trigonométrique faisant correspondre à l angle de deux axes la mesure de la projection orthogonale sur l un, d un vecteur unitaire porté par l autre; sinus de l angle complémentaire.… … Encyclopédie Universelle
Fonction cosinus — Fonction trigonométrique Pour les articles homonymes, voir Cosinus (homonymie), Tangente et Sinus. Toutes les valeurs des fonctions trigonométriques en u … Wikipédia en Français
Théorème du cosinus — Théorème d Al Kashi Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment… … Wikipédia en Français
Loi De Stefan-Boltzmann — La loi de Stefan Boltzmann ou de Stefan établit que la puissance totale rayonnée par unité de surface dans le demi espace libre du corps noir (exitance[1] énergétique du corps noir) s exprime par la formule : Où σ est la constante de Stefan… … Wikipédia en Français
Loi de Stefan — Boltzmann La loi de Stefan Boltzmann ou de Stefan établit que la puissance totale rayonnée par unité de surface dans le demi espace libre du corps noir (exitance[1] énergétique du corps noir) s exprime par la formule : Où σ est la constante… … Wikipédia en Français
Loi de stefan — Boltzmann La loi de Stefan Boltzmann ou de Stefan établit que la puissance totale rayonnée par unité de surface dans le demi espace libre du corps noir (exitance[1] énergétique du corps noir) s exprime par la formule : Où σ est la constante… … Wikipédia en Français
Loi de stefan-boltzmann — La loi de Stefan Boltzmann ou de Stefan établit que la puissance totale rayonnée par unité de surface dans le demi espace libre du corps noir (exitance[1] énergétique du corps noir) s exprime par la formule : Où σ est la constante de Stefan… … Wikipédia en Français
Loi De Cassie — La loi de Cassie décrit l angle de contact θc pour un liquide déposé sur une surface composite. Elle date de 1944 et permet d expliquer pourquoi un substrat plus grossier augmente l angle [1]. La description formelle est la suivante : avec… … Wikipédia en Français
Loi de cassie — La loi de Cassie décrit l angle de contact θc pour un liquide déposé sur une surface composite. Elle date de 1944 et permet d expliquer pourquoi un substrat plus grossier augmente l angle [1]. La description formelle est la suivante : avec… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Loi des cosinus

Théorème d'Al-Kashi

Sommaire

Histoire

Le théorème et ses applications