- Loi de Bernouilli
-
Loi de Bernoulli
Pour les articles homonymes, voir Théorème de Bernoulli.Bernoulli Densité de probabilité / Fonction de masse Fonction de répartition Paramètres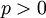 
(nombre réel)
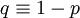
Support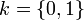 
Densité de probabilité (fonction de masse)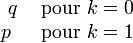 
Fonction de répartition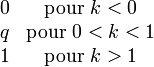 
Espérance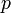 
Médiane (centre) non disponible Mode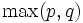 
Variance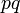 
Asymétrie (statistique)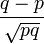 
Kurtosis (non-normalisé)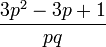 
Entropie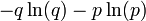 
Fonction génératrice des moments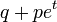 
Fonction caractéristique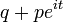 
En mathématiques, la distribution de Bernoulli ou loi de Bernoulli, du nom du mathématicien suisse Jacques Bernoulli, est une distribution discrète de probabilité, qui prend la valeur 1 avec la probabilité p et 0 avec la probabilité q = 1 − p.
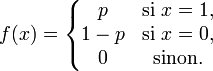
L'espérance mathématique d'une variable aléatoire de Bernoulli vaut p et la variance vaut pq = p(1 − p).
Le Kurtosis tend vers l'infini pour des valeurs hautes et basses de p, mais pour p = 1 / 2 la distribution de Bernoulli a un kurtosis plus bas que toute autre distribution, c’est-à-dire 1.
Variable de Bernoulli
Une variable aléatoire suivant la loi de Bernoulli est appelée variable de Bernoulli.
La loi de Bernoulli est la loi de la variable aléatoire qui code le résultat d'une épreuve de Bernoulli de la manière suivante : 1 pour "succès", 0 pour "échec", ou quel que soit le nom qu'on donne aux deux issues d'une épreuve de Bernoulli.
Plus généralement, toute application mesurable à valeur dans {0,1} est une variable de Bernoulli. Autrement dit, toute fonction indicatrice mesurable suit la loi de Bernoulli. Réciproquement, pour toute variable de Bernoulli X définie sur (Ω,A,P), on peut trouver un ensemble mesurable B tel que X et la fonction indicatrice de B soient presque sûrement égaux : toute variable de Bernoulli est presque sûrement égale à une fonction indicatrice.
Classiquement, écrire une variable aléatoire N, comptant un nombre d'évènements dans une situation donnée, comme la somme d'une famille de variables de Bernoulli permet de calculer simplement l'espérance de N, comme étant la somme des paramètres de ces variables de Bernoulli:
![\left\{N=\sum_{i\in I} X_i\right\}\quad\Rightarrow\quad\left\{\mathbb{E}[N]=\sum_{i\in I} \mathbb{P}(X_i=1)\right\}.](/pictures/frwiki/98/bd8297ce7dec883811c3a22f914f8fca.png)
Cette méthode simplifie aussi le calcul de la variance de N, dans certains cas.
Distributions liées
- Si
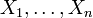sont des variables aléatoires de Bernoulli avec paramètre p, indépendantes et identiquement distribuées, alors leur somme N suit la Loi binomiale :
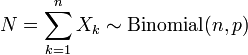
Voir aussi
Portail des probabilités et des statistiques
Catégorie : Loi de probabilité - Si
Wikimedia Foundation. 2010.
