- Lemme des tiroirs
-
Principe des tiroirs
En mathématiques, le principe des tiroirs, ou principe des tiroirs de Dirichlet, affirme que si n chaussettes occupent m tiroirs, et si n > m, alors au moins un tiroir doit contenir strictement plus d'une chaussette. Une autre formulation serait que m tiroirs ne peuvent contenir strictement plus de m chaussettes avec une seule chaussette par tiroir; ajouter une autre chaussette obligera à réutiliser l'un des tiroirs.
Mathématiquement, le principe des tiroirs peut s'énoncer ainsi :
- Si E et F sont deux ensembles finis, tels que card(E) > card(F) et si f : E→F est une application de E dans F, alors il existe un élément de F qui admet au moins deux antécédents par f ; autrement dit il n'existe pas d'application injective de E dans F.
Sommaire
Appellation
La première version du principe fut énoncée par Dirichlet en 1834 sous le nom de Schubfachprinzip (« principe du tiroir »), suite à une observation de ses chaussettes dans sa commode. Dans certains pays comme la Russie, ce principe s'appelle le principe de Dirichlet (à ne pas confondre avec le principe du maximum pour les fonctions harmoniques, du même nom). Ce principe est aussi appelé principe des tiroirs de Dirichlet-Schläfli.
En anglais, ce principe est appelé pigeonhole principle. Il fait référence à la répartition des pigeons dans les cases d'un pigeonnier.
Applications
Bien que le principe des tiroirs semble être une observation triviale, il peut être employé pour démontrer des résultats inattendus.
Par exemple, il doit y avoir au moins deux personnes à Dallas au Texas avec le même nombre de cheveux sur leur tête. Démonstration : une tête normale a environ 150 000 cheveux et il est raisonnable de supposer que personne n'a plus de 1 000 000 de cheveux sur la tête. Il y a plus de 1 000 000 personnes à Dallas. Si nous associons à chaque nombre de cheveux sur une tête un tiroir, et si nous plaçons chaque habitant de Dallas dans le tiroir correspondant à son nombre de cheveux sur la tête, alors d'après le principe des tiroirs, il y a nécessairement au moins deux personnes ayant exactement le même nombre de cheveux sur la tête à Dallas ! Évidemment, le résultat reste vrai pour n'importe quelle mégalopole.
Approximation d'un réel
Soit un réel x et un entier naturel n. Pour tout réel y, on note {y} la partie fractionnaire de y (c'est à dire la différence entre y et sa partie entière). Les (n + 1) éléments de [0,1[ définis par
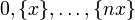se répartissent dans les n "tiroirs" [r / n,(r + 1) / n[, où 
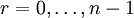. Il existe donc un entier r et deux entiers 
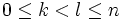tels que :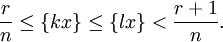
En notant p la différence des parties entières de kx et lx, on en déduit :
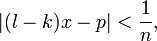
ou encore, en introduisant l'entier q = l − k, inférieur à n :
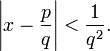
Généralisations
Une version généralisée de ce principe déclare que, si n objets discrets occupent m récipients, alors au moins un récipient doit contenir au moins
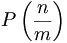objets où P est la fonction qui associe à un réel x le plus petit entier supérieur ou égal à x. Le nombre 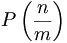est donc le plus petit entier supérieur ou égal à 
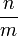, et peut s'écrire avec la fonction partie entière : 
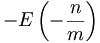.Le principe des tiroirs est un exemple d'argument de dénombrement. Ce principe peut être appliqué à de nombreux problèmes sérieux, y compris ceux qui impliquent des ensembles infinis qui ne peuvent pas être mis en correspondance univoque. En approximation diophantienne, l'application quantitative du principe montre l'existence de solutions entières d'un système d'équations linéaires et ce résultat porte le nom de lemme de Siegel.
Voir aussi
Portail des mathématiques
Catégories : Théorie des ensembles | Analyse combinatoire | Théorème de mathématiques
Wikimedia Foundation. 2010.
