Lemme De Lebesgue
Contenu soumis à la licence CC-BY-SA. Source : Article Lemme De Lebesgue de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Lemme de lebesgue — En mathématiques, le lemme de Lebesgue est un résultat important en théorie de l approximation. Il permet d obtenir une borne sur l erreur de projection. Enoncé Soit un espace vectoriel normé, U un sous espace vectoriel de V et soit P un… … Wikipédia en Français
Lemme de Lebesgue — En mathématiques, le lemme de Lebesgue est un résultat important en théorie de l approximation. Il permet d obtenir une borne sur l erreur de projection. Enoncé Soit un espace vectoriel normé, U un sous espace vectoriel de V et soit P un… … Wikipédia en Français
Lemme De Fatou — Le lemme de Fatou est un important résultat dans la théorie de l intégration de Lebesgue. Il a été démontré par le mathématicien français Pierre Fatou (1878 1929). Ce lemme traite d un cas où une propriété de convergence simple d une suite de… … Wikipédia en Français
Lemme de fatou — Le lemme de Fatou est un important résultat dans la théorie de l intégration de Lebesgue. Il a été démontré par le mathématicien français Pierre Fatou (1878 1929). Ce lemme traite d un cas où une propriété de convergence simple d une suite de… … Wikipédia en Français
Lemme De Recouvrement De Vitali — Le lemme de recouvrement de Vitali est un résultat combinatoire de théorie de l intégration des espaces euclidiens. Il est largement utilisé dans des démonstrations en analyse réelle. L idée basique du lemme est la suivante: supposons que l on… … Wikipédia en Français
Lemme de recouvrement de vitali — Le lemme de recouvrement de Vitali est un résultat combinatoire de théorie de l intégration des espaces euclidiens. Il est largement utilisé dans des démonstrations en analyse réelle. L idée basique du lemme est la suivante: supposons que l on… … Wikipédia en Français
Lemme de Riemann — Théorème de Riemann Lebesgue En analyse, le théorème de Riemann Lebesgue, parfois aussi appelé lemme de Riemann Lebesgue (ou encore lemme intégral de Riemann Lebesgue) est un résultat de théorie de Fourier. Il apparaît sous deux formes… … Wikipédia en Français
Lemme de Cousin — En mathématiques, le lemme de Cousin[1] est une propriété de la droite réelle équivalente à l existence de la borne supérieure pour les parties majorées de . Il joue un rôle important dans l intégrale de Kurzweil Henstock, mais permet également… … Wikipédia en Français
Lemme de Fatou — Le lemme de Fatou est un important résultat dans la théorie de l intégration de Lebesgue. Il a été démontré par le mathématicien français Pierre Fatou (1878 1929). Ce lemme compare l intégrale d une limite inférieure de fonctions mesurables… … Wikipédia en Français
Lemme de Scheffé — Ne doit pas être confondu avec Théorème de Lehman Scheffé. Le lemme de Scheffé (en) est un critère de convergence en loi concernant les suites de variables aléatoires à densité. Sommai … Wikipédia en Français
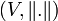 un espace vectoriel normé, U un sous-espace vectoriel de V et soit P un projecteur lineaire sur U. Alors, pour chaque
un espace vectoriel normé, U un sous-espace vectoriel de V et soit P un projecteur lineaire sur U. Alors, pour chaque 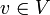 :
: