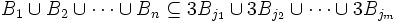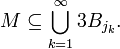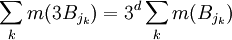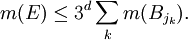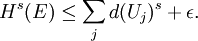Lemme de recouvrement de vitali

Lemme de recouvrement de Vitali

Le lemme de recouvrement de Vitali est un résultat combinatoire de théorie de l'intégration des espaces euclidiens. Il est largement utilisé dans des démonstrations en analyse réelle.

L'idée basique du lemme est la suivante: supposons que l'on ait une collection de cercles dans le plan, autorisés à se superposer. Alors il est possible d'en extraire une sous-collection dont les cercles ne s'intersectent pas, et si l'on multiplie par 3 leurs rayons, ces cercles recouvrent la collection initiale.

Enoncé

Version finie: Soit $B 1,..., B n$ une collection de boules de 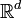$\mathbb{R}^{d}$ . Alors, il existe une sous-collection disjointe 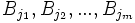$B_{j_{1}},B_{j_{2}},...,B_{j_{m}}$ de ces boules satisfaisant

$B_{1}\cup B_{2}\cup\cdots \cup B_{n}\subseteq 3B_{j_{1}}\cup 3B_{j_{2}}\cup\cdots \cup 3B_{j_{m}}$

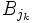où $3B_{j_{k}}$ dénotant la boule de même centre que $B_{j_{k}}$ mais ayant 3 fois son rayon.

Version infinie: Soit $M$ un ensemble borné de 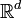$\mathbb{R}^{d}$ ; ${B j}$ une collection infinie (dénombrable ou non) de boules de 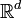$\mathbb{R}^{d}$ centrées en des points de $M$ et dont la réunion recouvre $M$ . Alors, il existe une sous-collection dénombrable de boules disjointes 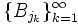$\{B_{j_{k}}\}_{k=1}^{\infty}$ de la collection initiale avec

$M\subseteq \bigcup_{k=1}^{\infty} 3B_{j_{k}}.$

Preuve

Dans la version finie :

Démonstration

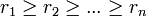Sans aucune perte de généralité et quitte à réordonner les indices des boules, on peut supposer qu'elles sont rangées par ordre de rayon décroissant, plus précisément si pour tout $k\in\{1,...,n\},\quad r_k$ désigne le rayon de la boule $B k$ alors $r_1\geq r_2\geq...\geq r_n$ . On pose $j 1 = 1$ et on retire toutes les boules qui ont une intersection non vide avec $B 1$ . On pose $j 2$ le plus grand entier parmi les indices des boules restantes si il y en a. On retire des boules restantes toutes les boules ayant une intersection non vide avec $B_{j_2}$ . On recommence ce processus qui s'arrête au bout d'un nombre de fini d'étapes (le nombre de boules étant fini). 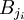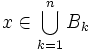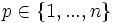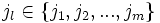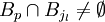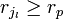On a alors une partie ${j 1, j 2,..., j m}$ de ${1,..., n}$ telle que les boules $B_{j_i}$ sont disjointes et si $x\in\bigcup_{k=1}^{n}B_k$ alors il existe $p\in\{1,...,n\}$ tel que $x\in B_p$ et par construction il existe $j_l\in\{j_1,j_2,...,j_m\}$ tel que $B_p\cap B_{j_l}\neq\empty$ et $r_{j_l}\geq r_p$ , en prenant 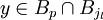$y\in B_p\cap B_{j_l}$ on a alors si $x p$ désigne le centre de $B p$ et 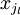$x_{j_l}$ le centre de 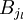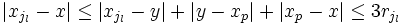$B_{j_l}$ : $|x_{j_l}-x|\leq|x_{j_l}-y|+|y-x_p|+|x_p-x|\leq 3r_{j_l}$ donc $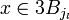x\in 3B_{j_l}$ et on a bien démontré que $\bigcup_{k=1}^{n}B_k\subset\bigcup_{i=1}^{m}3B_{j_i}$ .

Dans la version infinie :

Démonstration

On peut supposer sans perte de généralité que la famille des rayons est bornée. Sinon, comme le domaine est borné, une seule boule suffisamment grosse suffit à couvrir $M$ . On reproduit la preuve précédente en prendant à chaque fois une boule dont le rayon excède la moitié de la borne supérieure des boules qui n'intersectent pas la zone déjà couverte. Eventuellement, le procédé peut s'arrêter en temps fini si on a tout recouvert. Soit $B (x, r)$ une boule de la collection initiale. Si la séquence s'est arrêtée, il est clair qu'elle intersecte une des boules choisies, sinon on aurait pu continuer la séquence. Sinon, la suite des rayons tend vers 0 car on ne peut loger une infinité de boules disjointes de rayon minoré dans un domaine borné. Alors la boule $B (x, r)$ intersecte la suite des rayons des boules dès que cette séquence passe en dessous de r. Finalement, dans tout les cas, toute boule $B (x, r)$ de la famille intersecte une boule de rayon plus grand de la sous-famille extraite. Cela donne le résultat par l'inégalité triangulaire comme précédemment.

Applications

Une application directe du lemme de recouvrement de Vitali permet de prouver l'inégalité maximale de Hardy-Littlewood. Comme dans cette preuve, le lemme de Vitali est fréquemment utilisé lorsque, par exemple, on étudie la mesure de Lebesgue, $m$ , d'un ensemble 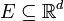$E\subseteq\mathbb{R}^{d}$ , que l'on sait être contenu dans l'union d'une certaine collection de boules ${B j}$ , chacune d'entre elles ayant une mesure pouvant être calculée aisément, ou ayant une propriété particulière que l'on souhaite exploiter. Donc, si l'on calcule la mesure de cette union, on aura une borne supérieure de la mesure de $E$ . Cependant, il est difficile de calculer la mesure de l'union de ces boules si elles se superposent. Avec les théorème de Vitali, on peut choisir une sous-collection 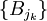$\{B_{j_{k}}\}$ disjointe. Alors, en triplant leur rayon, cette subcollection transformée contiendra le volume occupé par la collection de boules originale, et donc couvrira $E$ . On a donc,

$m(E)\leq m\left(\bigcup_{j}B_{j}\right) \leq m\left(\bigcup_{k}3B_{j_{k}}\right)\leq \sum_k m(3B_{j_{k}})$

Comme on triple le rayon d'une boule de dimension d revient à multiplier son volume par un facteur de $3 d$ , on a:

$\sum_k m(3B_{j_{k}})=3^d \sum_{k} m(B_{j_{k}})$

et donc:

$m(E)\leq 3^{d}\sum_{k}m(B_{j_{k}}).$

On peut utiliser cette approche en considérant la dimension de Hausdorff à la place de la mesure de Lebesgue. Dans ce cas, on obtient le théorème suivant.

Théorème de recouvrement de Vitali

Définition. Pour un ensemble 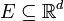$E\subseteq\mathbb{R}^{d}$ , on définit la classe de Vitali 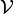$\mathcal{V}$ pour $E$ comme étant une collection d'ensembles tel que pour tout 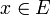$x\in E$ et $δ > 0$ il existe un ensemble 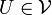$U\in\mathcal{V}$ tel que 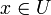$x\in U$ et le diamètre de $U$ est plus petit que $δ.$

Théoreme. Soit 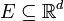$E\subseteq\mathbb{R}^{d}$ un ensemble $H s$ -mesurable et 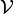$\mathcal{V}$ une classe de Vitali pour $E$ . Alors il existe une collection disjointe, dénombrable 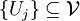$\{U_{j}\}\subseteq \mathcal{V}$ telle que soit

$H^{s}(E\backslash \bigcup_{j}U_{j})=0 \mbox{ ou }\sum_{j}d(U_{j})^{s}=\infty.$

De plus, si $E$ à une mesure de Hausdorff finie, alors pour tout $ε > 0$ , on peut choisir cette sous-collection ${U j}$ telle que

$H^{s}(E)\leq \sum_{j}d(U_{j})^{s}+\epsilon.$

Sources

(en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Vitali covering lemma ».
Measure theory and inegration, Michael E. Taylor, American Mathematical Society.
K. J. Falconer, The Geometry of Fractal Sets, Cambridge University Press, 1985.
Rami Shakarchi & Elias Stein, Princeton Lectures in Analysis III: Real Analysis, Princeton University Press, 2005.

Portail des mathématiques

Ce document provient de « Lemme de recouvrement de Vitali ».

Catégories : Théorie des ensembles | Lemme de mathématiques | Théorie de la mesure

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Lemme de recouvrement de vitali de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Lemme De Recouvrement De Vitali — Le lemme de recouvrement de Vitali est un résultat combinatoire de théorie de l intégration des espaces euclidiens. Il est largement utilisé dans des démonstrations en analyse réelle. L idée basique du lemme est la suivante: supposons que l on… … Wikipédia en Français
Lemme de recouvrement de Vitali — Le lemme de recouvrement de Vitali[1] est un résultat combinatoire de théorie de l intégration des espaces euclidiens. Il est largement utilisé dans des démonstrations en analyse réelle. L idée basique du lemme est la suivante : supposons… … Wikipédia en Français
Giuseppe Vitali — Pour les articles homonymes, voir Vitali. Giuseppe Vitali Giuseppe Vitali (né le 26 août 1875 à Ravenne, en Émilie Romagne mort le 29 février … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Fonction maximale de Hardy-Littlewood — En mathématiques et plus particulièrement en analyse, la fonction maximale de Hardy Littlewood est un opérateur mathématiques M qui associe à toute fonction intégrable une autre fonction Mf ; cette fonction Mf est définie en chaque point… … Wikipédia en Français
Théorème de différenciation de Lebesgue — En mathématiques, et plus particulièrement dans la théorie de l intégration, le théorème de différenciation de Lebesgue stipule que sous certaines conditions on peut retrouver une fonction en dérivant son intégrale, mais il faut avant tout… … Wikipédia en Français
Théorème de différentiation de Lebesgue — En mathématiques, et plus particulièrement dans la théorie de l intégration, le théorème de différentiation de Lebesgue stipule que sous certaines conditions on peut retrouver une fonction en dérivant son intégrale, mais il faut avant tout… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Lemme de recouvrement de vitali