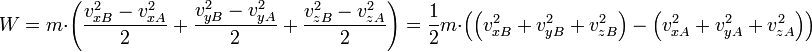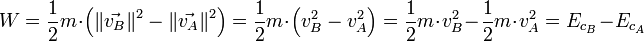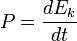- Kinétique
-
Énergie cinétique
L'énergie cinétique est l’énergie que possède un corps du fait de son mouvement. L’énergie cinétique d’un corps est égale au travail nécessaire pour faire passer le dit corps du repos à son mouvement de translation ou de rotation.
Sommaire
Historique
Article détaillé : vis viva.Gottfried Leibniz, s'opposant ainsi à Descartes, qui estimait que la quantité de mouvement se conservait toujours, développa l'idée de la « force vive » (vis viva), à laquelle il attribuait la valeur mv2. La force vive est donc le double de l'énergie cinétique.
« Il y a longtemps déjà que j’ai corrigé la doctrine de la conservation de la quantité de mouvement, et que j’ai posé à sa place quelque chose d’absolu, justement la chose qu’il faut, la force (vive) absolue… On peut prouver, par raison et par expérience, que c’est la force vive qui se conserve… » [1]
Définitions
Cas d'un point matériel
Dans le domaine de validité de la mécanique newtonienne, la notion d'énergie cinétique peut être facilement mise en évidence, pour un corps considéré comme ponctuel (ou point matériel) de masse m constante.
En effet, la relation fondamentale de la dynamique s'écrit :
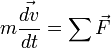 , avec
, avec 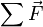 somme des forces appliquées au point matériel de masse m (y compris les "forces d'inertie" dans le cas d'un référentiel non galiléen).
somme des forces appliquées au point matériel de masse m (y compris les "forces d'inertie" dans le cas d'un référentiel non galiléen).En prenant le produit scalaire, membre à membre, par la vitesse
 du corps, il vient :
du corps, il vient :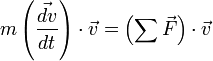 , or
, or 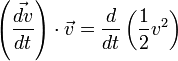 , il vient ainsi :
, il vient ainsi : 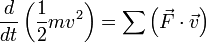 .
.On met en évidence dans le membre de gauche la quantité
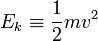 appelée énergie cinétique du point matériel, dont la variation est égale à la somme des puissances
appelée énergie cinétique du point matériel, dont la variation est égale à la somme des puissances 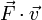 des forces appliquées au corps (théorème de l'énergie cinétique, forme "instantanée").
des forces appliquées au corps (théorème de l'énergie cinétique, forme "instantanée").On peut obtenir une expression plus générale en considérant que l'on a donc
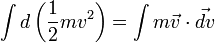 , puisque
, puisque 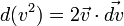 . En introduisant la variation infinitésimale de la quantité de mouvement du corps,
. En introduisant la variation infinitésimale de la quantité de mouvement du corps, 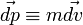 , il vient au final l'expression :
, il vient au final l'expression : 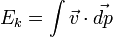 .
.Cas d'un système de points
Dans le cas d'un corps que l'on ne peut considérer ponctuel, il est possible de l'assimiler à un système (d'une infinité) de points matériels Mi de masses mi avec
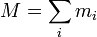 masse totale du corps.
masse totale du corps.L'énergie cinétique Ek du système de points peut être alors simplement définie comme la somme des énergies cinétiques associées aux points matériels constituant le système :
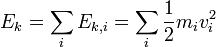 , (1). Cette expression est générale et ne préjuge pas de la nature du système, déformable ou pas.
, (1). Cette expression est générale et ne préjuge pas de la nature du système, déformable ou pas.Remarque : en considérant la limite des milieux continus on a
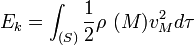 , M étant un point courant du système (S).
, M étant un point courant du système (S).Unité
L'unité légale est le joule. Les calculs s'effectuent avec les masses en kg et les vitesses en
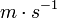 .
.Théorème de König
L'expression (1) n'est guère utilisable directement, bien que générale. Il est possible de la réécrire sous une autre forme, dont l'interprétation physique est plus aisée.
Enoncé
Ce théorème se démontre en faisant intervenir le référentiel barycentrique (R*) lié au centre d'inertie G du système, et en mouvement de translation par rapport au référentiel d'étude (R). Il s'écrit:
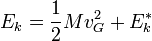 .
.L'énergie cinétique d'un système est alors la somme de deux termes: l'énergie cinétique du centre de masse de (S) affectée de sa masse totale M,
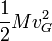 , et l'énergie cinétique propre du système dans (R*),
, et l'énergie cinétique propre du système dans (R*), 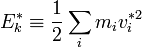 .
.Application à un solide
Un solide est un système de points tels que les distances entre deux points quelconques de (S) sont constantes. Il s'agit d'une idéalisation d'un solide réel, considéré comme absolument rigide.
Cas général : axe instantané de rotation
Dans ce cas, le mouvement du solide peut être décomposé en un mouvement de son centre de masse G dans (R) et un mouvement de rotation autour d'un axe instantané (Δ) dans le référentiel barycentrique (R*).
Plus précisément, pour un solide on peut écrire le champ des vitesses dans le référentiel barycentrique (R*) sous la forme
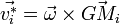 ,
, 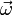 étant le vecteur rotation instantané du solide dans (R*) [ou (R), puisque les deux référentiels sont en translation]. Son énergie cinétique propre
étant le vecteur rotation instantané du solide dans (R*) [ou (R), puisque les deux référentiels sont en translation]. Son énergie cinétique propre 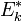 s'exprime alors
s'exprime alors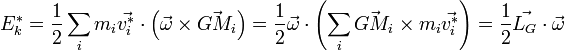 ,
,
puisque
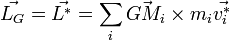 , moment cinétique du solide par rapport à G, égal au moment cinétique propre
, moment cinétique du solide par rapport à G, égal au moment cinétique propre 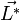 (voir théorèmes de König).
(voir théorèmes de König).D'après le théorème de König, l’énergie cinétique totale d’un solide s'écrit donc ainsi:
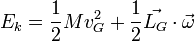 ,
,que l'on peut considérer comme la somme d’une énergie cinétique "de translation" et d’une énergie cinétique de rotation
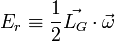 , aussi appelée énergie cinétique angulaire.
, aussi appelée énergie cinétique angulaire.Cas de la rotation autour d'un axe fixe
Si, de surcroît, il y a rotation autour d'un axe (Δ) fixe dans (R), le moment cinétique par rapport à G du solide s'écrit
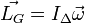 , où IΔ est le moment d'inertie du solide par rapport à l'axe de rotation (Δ). Son énergie cinétique de rotation se mettra ainsi sous la forme:
, où IΔ est le moment d'inertie du solide par rapport à l'axe de rotation (Δ). Son énergie cinétique de rotation se mettra ainsi sous la forme: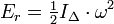 .
.
En mécanique relativiste
Dans la théorie de la relativité d’Einstein (utilisée principalement pour les vitesses proches de la vitesse de la lumière, mais valable pour toutes vitesses), l’énergie cinétique est :
- Ek = mc2(γ − 1) = γmc2 − mc2
- Avec :
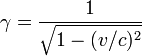 ; (le facteur relativiste)
; (le facteur relativiste)
- Ek : l’énergie cinétique du corps (dans le référenciel considéré) ;
- v : la vitesse du corps (dans le référenciel considéré) ;
- m : sa masse au repos (dans son référenciel) ;
- c : la vitesse de la lumière dans le vide (dans TOUT référenciel) ;
- γmc2 : l’énergie totale du corps (dans le référenciel considéré) ;
- mc2 est l’énergie au repos (90 pétajoules par kilogramme) exprimée en unités conventionnelles.
La théorie de la relativité affirme que l’énergie cinétique d’un objet (ayant une masse « au repos[2]» non nulle) tend vers l’infini quand sa vitesse s’approche de la vitesse de la lumière et que, par conséquent, il est impossible d’accélérer un objet jusqu’à cette vitesse.
On peut montrer que le rapport de l’énergie cinétique relativiste sur l’énergie cinétique newtonienne tend vers 1 quand la vitesse v tend vers 0, i.e.,
Ce résultat peut être obtenu par un développement limité au premier ordre du rapport. Le terme de second ordre est 0,375 mv4/c4, c’est-à-dire que, pour une vitesse de 10 km/s il vaut 0,04 J/kg, et que, pour une vitesse de 100 km/s il vaut 40 J/kg, etc.
Quand la gravité est faible et que l’objet se déplace à des vitesses très inférieures à la vitesse de la lumière (c’est le cas de la plupart des phénomènes observés sur Terre), la formule de la mécanique newtonienne est une excellente approximation de l’énergie cinétique relativiste.
Théorème de l’énergie cinétique
Ce théorème, valable uniquement dans le cadre de la mécanique newtonienne, permet de lier l’énergie cinétique d’un système au travail des forces auxquelles celui-ci est soumis.
Énoncé
Dans un référentiel galiléen, pour un corps ponctuel de masse m constante parcourant un chemin reliant un point A à un point B, la variation d’énergie cinétique est égale à la somme W des travaux des forces extérieures et intérieures qui s’exercent sur le solide en question :
où EkA et EkB sont respectivement l’énergie cinétique du solide aux points A et B.
Démonstration
D’après la 2e loi de Newton, l’accélération du centre de gravité est liée aux forces qui s’exercent sur le solide par la relation suivante :
Pendant une durée dt, le solide se déplace de
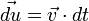 où
où  est la vitesse du solide. On en déduit le travail élémentaire des forces :
est la vitesse du solide. On en déduit le travail élémentaire des forces :Si le solide parcourt un chemin d’un point A à un point B, alors le travail total s’obtient en faisant une intégrale le long du chemin :
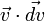 étant une différentielle totale, l’intégrale ne dépend pas du chemin suivi entre A et B et peut donc être obtenue explicitement :
étant une différentielle totale, l’intégrale ne dépend pas du chemin suivi entre A et B et peut donc être obtenue explicitement :Théorème de la puissance cinétique
Dans un référentiel galiléen, la puissance des forces s'appliquant au point M est égale à la dérivée par rapport au temps de l'énergie cinétique.
L’énergie thermique en tant qu’énergie cinétique
L’énergie thermique est une forme d’énergie due à l’énergie cinétique totale des molécules et des atomes qui forment la matière. La relation entre la chaleur, la température et l’énergie cinétique des atomes et des molécules est l’objet de la mécanique statistique et de la thermodynamique.
De nature quantique, l’énergie thermique se transforme en énergie électromagnétique par le phénomène de rayonnement du corps noir.
La chaleur, qui représente un échange d’énergie thermique, est aussi analogue à un travail dans le sens où elle représente une variation de l’énergie interne du système. L’énergie représentée par la chaleur fait directement référence à l’énergie associée à l’agitation moléculaire. La conservation de la chaleur et de l’énergie mécanique est l’objet du premier principe de la thermodynamique.
Articles détaillés : Constante de Boltzmann et capacité calorique spécifique.Notes et références
Voir aussi
- Portail de la physique
- Portail du génie mécanique
Catégories : Mécanique classique | Énergie
Wikimedia Foundation. 2010.

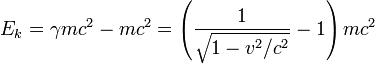
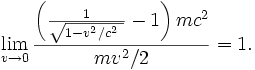
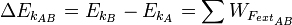
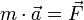
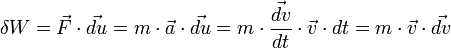
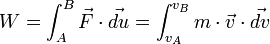
![W=m\cdot\int_{v_A}^{v_B}\vec{v}\cdot\vec{dv} = m\cdot\left (\int_{v_{xA}}^{v_{xB}}v_x\cdot dv_x+\int_{v_{yA}}^{v_{yB}}v_y\cdot dv_y+\int_{v_{zA}}^{v_{zB}}v_z\cdot dv_z\right )=m\cdot\left (\left[ \frac{v_x^2}{2} \right]_{v_{xA}}^{v_{xB}}+\left[ \frac{v_y^2}{2} \right]_{v_{yA}}^{v_{yB}}+\left[ \frac{v_z^2}{2} \right]_{v_{zA}}^{v_{zB}}\right )](/pictures/frwiki/102/fc56f4a458cbcf16b949629b5facb79a.png)