Itération De Halley
- Itération De Halley
-
Itération de Halley
En analyse numérique, l'itération de Halley ou méthode de Halley est un algorithme de recherche d'un zéro d'une fonction utilisé pour les fonctions d'une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2).
L'algorithme est itératif et de convergence cubique.
Il doit son nom à son inventeur, l'astronome Edmund Halley.
Énoncé
Soit f une fonction C² et a un zéro de f. La méthode de Halley consiste à itérer
![x_{n+1} = x_n - \frac {2 f(x_n) f'(x_n)} {2 {[f'(x_n)]}^2 - f(x_n) f''(x_n)}](/pictures/frwiki/54/623d63e2dca42f0d7217b203e14c3a9e.png)
à partir d'une valeur x0 proche de a.
Au voisinage de a, la suite vérifie :
- | xn + 1 − a | < K | xn − a | 3,
avec K > 0 ; ce qui signifie que la convergence est donc (au pire) cubique.
Déduction
La formule se déduit par exemple de la méthode de Newton appliquée à la fonction 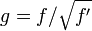 :
:
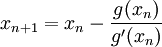 ,
,
avec
![g'(x) = \frac {2 {[f'(x)]}^2 - f(x) f''(x)} {2 f'(x) \sqrt{f'(x)}},](/pictures/frwiki/99/cf298dda630cc2b3fba30745dab3d52f.png)
d'où le résultat. Si f′(c) = 0, cela ne s'applique que si g peut être prolongée en c.
Voir aussi
Liens internes
Liens externes
 Portail des mathématiques
Portail des mathématiques
Catégorie : Algorithme de recherche d'un zéro d'une fonction
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Itération De Halley de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Iteration de Halley — Itération de Halley En analyse numérique, l itération de Halley ou méthode de Halley est un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e … Wikipédia en Français
Itération de Halley — En analyse numérique, l itération de Halley ou méthode de Halley est un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2). L algorithme… … Wikipédia en Français
Itération de halley — En analyse numérique, l itération de Halley ou méthode de Halley est un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2). L algorithme… … Wikipédia en Français
Iteration de Householder — Itération de Householder En analyse numérique, l itération de Householder ou méthode de Householder désigne un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée… … Wikipédia en Français
Itération De Householder — En analyse numérique, l itération de Householder ou méthode de Householder désigne un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2).… … Wikipédia en Français
Itération de Householder — En analyse numérique, l itération de Householder ou méthode de Householder désigne un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2).… … Wikipédia en Français
Itération de householder — En analyse numérique, l itération de Householder ou méthode de Householder désigne un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2).… … Wikipédia en Français
Halley-Verfahren — Das Halley Verfahren (auch Verfahren der berührenden Hyperbeln) ist, ähnlich wie das Newton Verfahren, eine Methode der numerischen Mathematik zur Bestimmung von Nullstellen f(x)=0 reeller Funktionen . Im Gegensatz zum Newton Verfahren hat es die … Deutsch Wikipedia
Fixed point iteration — In numerical analysis, fixed point iteration is a method of computing fixed points of iterated functions.More specifically, given a function f defined on the real numbers with real values and given a point x 0 in the domain of f, the fixed point… … Wikipedia
Racine carrée de deux — La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu’il est multiplié par lui même, donne le nombre 2, autrement dit √2 × √2 = 2. C’est un nombre irrationnel, dont une valeur approchée à 10 9… … Wikipédia en Français
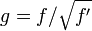 :
: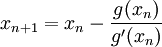 ,
,
![x_{n+1} = x_n - \frac {2 f(x_n) f'(x_n)} {2 {[f'(x_n)]}^2 - f(x_n) f''(x_n)}](/pictures/frwiki/54/623d63e2dca42f0d7217b203e14c3a9e.png)
![g'(x) = \frac {2 {[f'(x)]}^2 - f(x) f''(x)} {2 f'(x) \sqrt{f'(x)}},](/pictures/frwiki/99/cf298dda630cc2b3fba30745dab3d52f.png)