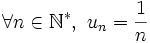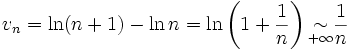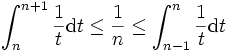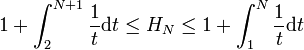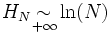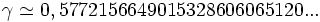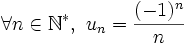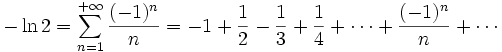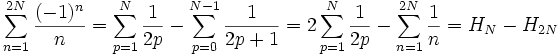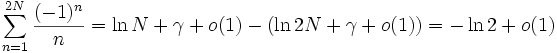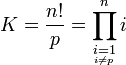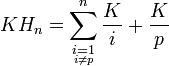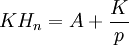Serie harmonique

Série harmonique

Pour les articles homonymes, voir Série et Harmonique.

En mathématiques, la série harmonique est une série de nombres réels. C'est la série des inverses des entiers naturels non nuls.

Sujet d'étude classique en analyse, elle fait partie de la famille plus large des séries de Riemann, qui permettent de déterminer la nature de nombreuses séries, par les théorèmes de comparaison.

Définition

Le terme général $(u n)$ de la série harmonique est défini par

$\forall n \in \N^*,\ u_n=\frac{1}{n}$

On note classiquement $H n$ la n-ième somme partielle de la série harmonique, qui est donc égale à

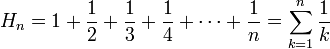$H_n=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n} = \sum_{k=1}^{n} \frac{1}{k}$ .

La série harmonique diverge

Expérimentation

En calculant les premières sommes partielles de la série harmonique, il apparaît que la suite de nombres obtenus est croissante et ne bouge pas très vite. On a même l'impression au bout d'un moment qu'elle est presque stationnaire.

On peut donc suspecter au premier abord cette série d'être une série convergente.

Valeur de n	Valeur de H_n	Valeur de n	Valeur de H_n
1	1	11	3,019877345
2	1,5	12	3,103210678
3	1,833333333	13	3,180133755
4	2,083333333	14	3,251562327
5	2,283333333	15	3,318228993
6	2,45	16	3,380728993
7	2,592857143	17	3,439552523
8	2,717857143	18	3,495108078
9	2,828968254	19	3,547739657
10	2,928968254	20	3,597739657

Réalité mathématique

En fait, la série harmonique diverge, elle tend vers $+\infty$ .

Valeur de n	Valeur de H_n
10	2,928968254
100	5,187377518
1 000	7,485470861
10 000	9,787606036
100 000	12,09014613
1 000 000	14,39272672

Dans le tableau ci-dessus, à chaque fois qu'on multiplie la valeur de n par 10, il semble qu'on rajoute une constante à H_n, de l'ordre de 2,3. Ce comportement apparent est de type logarithmique en n. C'est bien ce qu'on obtient on faisant une étude asymptotique plus poussée.

Démonstration

Cette série croissante ne peut avoir que deux types de comportement : ou bien elle converge ou bien elle diverge et tend vers + ∞. On raisonne par l'absurde. Supposons que la suite $H n$ converge vers $l$ . Dans ce cas, on sait aussi que la suite extraite $H 2 n$ converge aussi vers $l$ . Par conséquent, la suite $H 2 n - H n$ converge vers $0$ .

Or, on a les inégalités suivantes :

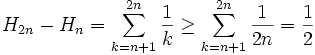$H_{2n}-H_{n} = \sum_{k=n+1}^{2n} \frac{1}{k} \geq \sum_{k=n+1}^{2n} \frac{1}{2n}=\frac{1}{2}$ .

On aboutit à une contradiction.

Autres démonstrations

On peut comparer la série harmonique à une série télescopique bien choisie

$v_n = \ln(n+1)-\ln n = \ln \left(1+\frac{1}{n}\right)\underset{+\infty}{\sim} \frac {1}{n}$

Alors $v n$ est le terme général d'une série divergente, à termes positifs, donc par comparaison la série harmonique diverge elle aussi.

On peut aussi montrer le résultat à l'aide de la méthode de comparaison série-intégrale (c'est un peu ce qui est caché, d'ailleurs dans le choix « judicieux » de la série télescopique).

Développement asymptotique de $H n$

Tous les termes du développement asymptotique peuvent s'obtenir par la méthode de comparaison série-intégrale.

Équivalent de $H n$

En utilisant l'encadrement suivant, lié à la décroissance de la fonction inverse (t donne 1/t)

$\int_n^{n+1} \frac {1}{t} \mathrm{d}t\leq \frac {1}{n} \leq \int_{n-1}^{n} \frac {1}{t} \mathrm{d}t$

Et en sommant de 2 à n et en ajoutant 1, on arrive à

$1+\int_2^{N+1}\frac {1}{t} \mathrm{d}t \leq H_N \leq 1+ \int_1^{N}\frac {1}{t} \mathrm{d}t$

Puis en calculant les deux membres et en constatant qu'ils sont tous deux équivalents à $ln n$

$H_N \underset{+\infty}{\sim} \ln(N)$

Second terme du développement asymptotique

De plus en continuant l'expérimentation avec sa calculatrice, l'on peut calculer les premier termes de la suite 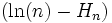$\ (\ln (n)- H_n)$ . On peut alors s'apercevoir assez rapidement que cette série semble tendre vers une limite finie.

Cette fois nous ne nous sommes pas trompés : on peut prouver que cette suite admet effectivement une limite finie. On a donc la formule d'Euler

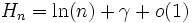$\ H_n = \ln (n)+\gamma +o(1)$ ,

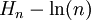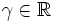C'est-à-dire que la suite $\ H_n - \ln(n)$ tend vers une certaine limite $\gamma \in \R$ .

Cette valeur $γ$ a été baptisée constante d'Euler-Mascheroni. Voici les 25 premiers chiffres de son développement décimal

$\gamma \simeq 0,5772156649015328606065120...$

Pour la démonstration de la formule d'Euler, et la généralisation à d'autres séries, voir l'article comparaison série-intégrale.

Généralisation et terme général du développement asymptotique

La méthode est détaillée dans l'article comparaison série-intégrale ; les premiers termes du développement sont

$\sum_{k=1}^n \frac1k= \ln(n)+\gamma+\frac1{2n}-\frac1{12n^2}+\frac1{120n^4}-\frac1{252n^6}+\frac1{240n^8}-\frac1{132n^{10}}+ O\left(\frac1{n^{12}}\right)$

La série harmonique alternée

Le terme général $(u n)$ de la série harmonique alternée est définie par

$\forall n \in \N^*,\ u_n=\frac{(-1)^n}{n}$

C'est donc une variante de la série harmonique. L'alternance des signes change tout puisque cette série converge, par le critère de convergence des séries alternées. On peut se servir de l'étude effectuée avec la série harmonique pour déterminer la nature et la somme de la série harmonique alternée.

En séparant termes pairs et impairs dans le calcul des sommes partielles, et en appliquant la formule d'Euler précédente, on prouve que la série harmonique alternée converge et a pour somme

$-\ln 2 = \sum_{n=1}^{+\infty} \frac{(-1)^n}{n}=-1+\frac{1}{2}-\frac{1}{3}+\frac{1}{4}+\cdots+\frac{(-1)^n}{n}+\cdots$

Démonstration détaillée : on décompose les sommes partielles d'ordre pair

$\sum_{n=1}^{2N} \frac1{n}=\sum_{p=1}^{N} \frac{1}{2p}+\sum_{p=0}^{N-1} \frac{1}{2p+1}$

$\sum_{n=1}^{2N} \frac{(-1)^n}{n}=\sum_{p=1}^{N} \frac{1}{2p}-\sum_{p=0}^{N-1} \frac{1}{2p+1} =2\sum_{p=1}^{N} \frac{1}{2p}-\sum_{n=1}^{2N} \frac1{n}=H_N-H_{2N}$

Une formule d'Euler pour chaque terme

$\sum_{n=1}^{2N} \frac{(-1)^n}{n}=\ln N+\gamma+o(1)-(\ln 2N+\gamma+o(1)) =-\ln 2+o(1)$

Pour conclure il faut encore signaler que si on prend une somme partielle d'ordre impair, elle a aussi pour limite - ln 2 (on ajoute en effet à la somme d'ordre pair précédente un terme qui tend vers 0).

Variante : on peut utiliser la théorie des séries entières en établissant la formule plus générale

$\forall x \in [-1,1[,\ -\ln (1-x)= \sum_{n=1}^{+\infty} \frac{x^n}{n}$

Série harmonique et entier naturel

Pour tout entier 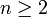$n \geq 2$ , $H n$ n'est jamais entier.

L'argumentation s'appuie sur le postulat de Bertrand : pour tout entier $k \geq 1$ , il existe un nombre premier $p$ compris (au sens large) entre $k + 1$ et $2 k$ .

Soit 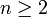$n \geq 2$ , et soit $k$ la partie entière de $n / 2$ . Il existe donc un nombre premier $p$ compris entre $k + 1$ et $2 k$ . Ce nombre premier $p$ est donc inférieur à $n$ et son double est strictement supérieur à $n$ . On en déduit que $p$ ne divise alors aucun des entiers de 1 à $n$ sauf lui-même.

Soit l'entier $K$ vérifiant

$K = \frac{n!}{p} = \prod_{\underset{ i \ne p}{i=1}}^n i$

D'après la remarque précédente, $p$ ne divise aucun des entiers de 1 à $p$ sauf lui-même, il ne divise donc pas leur produit, il ne divise donc pas $K$ .

On multiplie alors $H n$ par $K$

$KH_n = \sum_{\underset{ i \ne p}{i=1}}^n \frac Ki + \frac Kp$

Or pour tout 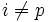$i \neq p$ , $K / i$ est un entier donc la somme des $K / i$ est un entier noté $A$ , donc

$KH_n = A + \frac Kp$

$A$ est un entier, $K / p$ n'est pas entier donc $K H n$ n'est pas entier et $H n$ n'est pas entier.

Voir aussi

Portail des mathématiques

Ce document provient de « S%C3%A9rie harmonique ».

Catégorie : Série

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Serie harmonique de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Série harmonique — Pour les articles homonymes, voir Série et Harmonique. En mathématiques, la série harmonique est une série de nombres réels. C est la série des inverses des entiers naturels non nuls. Elle fait partie de la famille plus large des séries de… … Wikipédia en Français
série harmonique — harmoninė eilutė statusas T sritis fizika atitikmenys: angl. harmonic series vok. harmonische Reihe, f rus. гармонический ряд, m pranc. série harmonique, f … Fizikos terminų žodynas
Série harmonique (mathématiques) — Nombre harmonique En mathématiques, les nombres harmoniques d ordre sont donnés par . Le cas particulier est fréquemment écrit sans l exposant, sous la forme . À la limite , l … Wikipédia en Français
harmonique — [ armɔnik ] adj. et n. m. ou f. • XIVe; lat. harmonicus, gr. harmonikos 1 ♦ Qui concourt à l harmonie musicale. ♢ Se dit de certains sons, de certains rapports ou assemblages de sons caractéristiques, en harmonie. Gamme, échelle harmonique. ⇒… … Encyclopédie Universelle
Série numérique — Série (mathématiques) Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L étude des séries consiste à effectuer la somme d un nombre fini … Wikipédia en Français
Série semi-convergente — Série (mathématiques) Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L étude des séries consiste à effectuer la somme d un nombre fini … Wikipédia en Français
série — [ seri ] n. f. • 1715; lat. series, spécialisé dès le XVIIe en math. 1 ♦ Math. Somme d un nombre fini de termes. Série harmonique : somme des inverses des entiers. Série convergente, telle que la somme de ses n premiers termes tend vers une… … Encyclopédie Universelle
Serie de Bertrand — Série de Bertrand Pour α et β deux réels, on appelle série de Bertrand la série à termes réels positifs suivante : . La série harmonique en est un cas particulier (au premier terme près), pour α = 1 et β = 0 … Wikipédia en Français
Série de bertrand — Pour α et β deux réels, on appelle série de Bertrand la série à termes réels positifs suivante : . La série harmonique en est un cas particulier (au premier terme près), pour α = 1 et β = 0 … Wikipédia en Français
Serie alternee — Série alternée En mathématiques, et plus particulièrement en analyse, une série alternée est un cas particulier de série à coefficients réels, dont la forme particulière permet d avoir des résultats de convergence notables. Une série à… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Serie harmonique

Série harmonique

Sommaire

Définition