- Inductance électrique
-
Inductance
L'inductance d’un circuit électrique est un coefficient qui traduit le fait qu’un courant le traversant crée un champ magnétique à travers la section entourée par ce circuit. Il en résulte un flux du champ magnétique à travers la section limitée par ce circuit.
L’inductance est égale au quotient du flux de ce champ magnétique par l’intensité du courant traversant le circuit. L’unité de l’inductance est le henry (H).
Par extension, on désigne par inductance tout circuit électrique ou dipôle électrique qui par sa construction a une certaine valeur d’inductance (grandeur physique). Ces dipôles sont généralement des bobines, souvent appelées inductances ou self (en anglais self inductance qui a donné le mot « self ») par abus de langage (ou métonymie) comme pour la résistance.
Sommaire
Inductance propre
La définition la plus courante d'inductance propre est la suivante : La surface circonscrite par un circuit électrique parcouru par un courant I est traversée par le flux du champ magnétique (appelé autrefois flux d’induction)
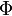 . L’inductance L du circuit électrique est alors définie comme le rapport entre le flux embrassé par le circuit et le courant :
. L’inductance L du circuit électrique est alors définie comme le rapport entre le flux embrassé par le circuit et le courant :Il est important de préciser que le flux
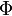 en question est celui produit par le courant I et non celui provenant d'une autre source (courant, aimant, etc.).
en question est celui produit par le courant I et non celui provenant d'une autre source (courant, aimant, etc.).Malgré sa popularité, cette définition présente deux inconvénients. Le premier est que la définition de l'inductance est donnée en fonction du flux
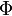 qui est une grandeur physique inaccessible directement. Il n'existe pas de moyen de mesurer le flux magnétique sans le faire varier en fonction du temps. Le second inconvénient est que la « surface circonscrite par le circuit » n'est pas toujours facile à déterminer et, dans certains cas, elle n'existe même pas (par exemple si le circuit « fait un nœud »).
qui est une grandeur physique inaccessible directement. Il n'existe pas de moyen de mesurer le flux magnétique sans le faire varier en fonction du temps. Le second inconvénient est que la « surface circonscrite par le circuit » n'est pas toujours facile à déterminer et, dans certains cas, elle n'existe même pas (par exemple si le circuit « fait un nœud »).Une deuxième définition qui ne présente pas ces inconvénients est :
où :
- L est l'inductance propre du circuit ou composant.
- u est la tension aux bornes du circuit.
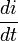 est la variation du courant qui traverse le circuit avec le temps (mesurée en ampères/seconde).
est la variation du courant qui traverse le circuit avec le temps (mesurée en ampères/seconde).- u et i sont des valeurs instantanées.
nous remarquons que :
- Lorsque le courant est constant, di/dt est nul et par conséquent la tension u auto-induite est nulle aussi.
- Le signe (-) indique que la tension auto-induite aux bornes de l'inductance s'oppose aux variations du courant qui la traverse.
- Quand on applique une tension constante à une inductance, le courant qui rentre par l'extrémité positive augmente avec le temps.
Ce n'est qu'en utilisant cette définition que l'on pourrait mesurer la valeur de l'inductance d'un circuit et, à partir de là, déterminer le flux magnétique équivalent qui traverse la « surface circonscrite » équivalente mais il faudrait pour cela que la tension aux bornes de cette portion de circuit ne dépende que de phénomènes magnétiques. Malheureusement celle -ci dépend d'un grand nombre d'effets physiques très divers (dont l'effet Joule), ce qui empêche toute mesure éventuelle de l'inductance d'une portion de circuit
De plus, cette définition n'est pas valable pour des portions de circuit présentant des non-linéarités (par exemple : des inductances à noyau ferromagnétique). La valeur de l'inductance dépendra alors de la valeur du courant et de son histoire (hystérésis).
Une partie du flux produit par le courant traverse le câble lui-même. Il convient donc de distinguer l’inductance externe et l’inductance interne d’un circuit. L’inductance interne d’un câble diminue lorsque la fréquence du courant augmente à cause de l’effet pelliculaire ou effet de peau. En pratique, l'effet de peau est presque complet à partir d'une ou deux dizaines de kilohertzs et l'inductance ne varie plus.
Inductance mutuelle
Lorsqu’un circuit 1 traversé par un courant noté
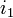 , produit un champ magnétique à travers un circuit 2, on peut écrire :
, produit un champ magnétique à travers un circuit 2, on peut écrire :La valeur de cette inductance mutuelle dépend des deux circuits en présence (caractéristiques géométriques, nombre de spires) mais aussi de leur position relative : éloignement et orientation.
Le dipôle « Inductance », ou bobine
Son symbole dans les schémas est L. Une inductance L est un dipôle tel que :
Cette relation vient de l’expression du flux du champ magnétique et de la loi de Faraday qui seront vues en magnétostatique :
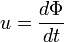 et de
et de 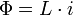
Cette équation montre que l’intensité du courant traversant une inductance ne peut pas subir de discontinuité, cela correspondrait en effet à une tension infinie à ses bornes, donc à une puissance infinie.
Puissance instantanée
Remarque : on ne peut stocker que de l'énergie. Le terme puissance emmagasinée est donc un abus de langage qui correspond en réalité à la puissance que l'on fournit à l'inductance et qui vient augmenter l'énergie emmagasinée dans cette dernière.
La puissance instantanée fournie à l'inductance est égale à :
En utilisant la transformation mathématique suivante :
on obtient la relation :
La puissance instantanée fournie à une inductance est liée à la variation du carré de l’intensité qui la traverse : si celui-ci augmente, l’inductance emmagasine de l'énergie. Elle en restitue dans le cas contraire.
L’énergie échangée entre 2 instants ti et tf vaut :
Il en résulte qu’il est difficile de faire varier rapidement le courant qui circule dans une bobine et ceci d’autant plus que la valeur de son inductance sera grande. Cette propriété est souvent utilisée pour supprimer de petites variations de courant non désirées.
L’effet de l’inductance face aux variations du courant est analogue en mécanique à l’effet de la masse face aux variations de la vitesse : quand on veut augmenter la vitesse il faut fournir de l’énergie cinétique et ceci d’autant plus que la masse est grande. Quand on veut freiner, il faut récupérer cette énergie. Débrancher une bobine parcourue par un courant, c’est un peu arrêter une voiture en l’envoyant contre un mur.
Puissance en régime sinusoïdal
En régime sinusoïdal, une inductance idéale (dont la résistance est nulle) ne consomme pas de puissance active. En revanche, il y a stockage ou restitution d’énergie par la bobine lors des variations de l'intensité du courant.
Impédance
A chaque instant
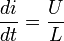 .
.On a
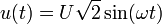 et
et 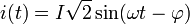 .
.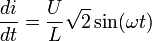
Donc
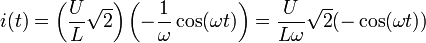
On obtient finalement :
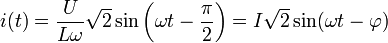 . Donc :
. Donc : 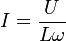 .
.- Loi d'Ohm en valeurs efficaces :
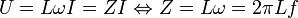 avec Z en Ohms, L en Henrys, ω en rad/s et f en Hz.
avec Z en Ohms, L en Henrys, ω en rad/s et f en Hz.
- En continu, f = 0: une bobine parfaite se comporte comme un court-circuit (en effet :
![Z = 0 \Rightarrow U = 0\cdot I = 0[V]](/pictures/frwiki/49/1703b94d5ded1d9b72d60462edccfe63.png) ).
).
En complexes
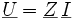 avec
avecD'où :
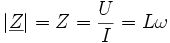 ; et
; et 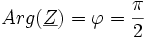
On en déduit que
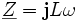 avec
avec 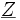 imaginaire pur de la forme
imaginaire pur de la forme 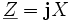 et X = Lω > 0.
et X = Lω > 0.Ouverture du circuit
Les inductances s'opposant à la variation du courant qui les traverse, l'ouverture d'un circuit inductif parcouru par un courant peut amener des surtensions. Ces surtensions oscillent avec une pulsation
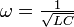 .
. 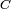 représentant les capacités parasites du circuit. La tension maximale de l'oscillation peut être très élevée. Ceci vient du fait qu'après l'interruption du courant l'énergie de l'inductance
représentant les capacités parasites du circuit. La tension maximale de l'oscillation peut être très élevée. Ceci vient du fait qu'après l'interruption du courant l'énergie de l'inductance 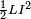 a été transférée aux capacités parasites sous la forme
a été transférée aux capacités parasites sous la forme 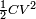 .
.Voir aussi
Liens internes
Liens externes
- Portail de l’électricité et de l’électronique
- Portail de la physique
Catégories : Théorie électrique | Grandeur physique
Wikimedia Foundation. 2010.


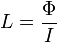
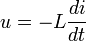
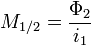
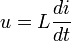
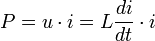
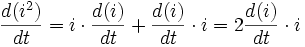
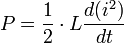
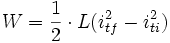

![\underline{U} = [U, 0]](/pictures/frwiki/97/a022edbfa88f01df2752797598dd9f90.png)
![\underline{I} = [I = \frac{U}{L\omega}, -\frac{\pi}{2} rad]](/pictures/frwiki/100/d09820292aa0405a8fa69b05eb6141e2.png)