Indice de réfraction

Image animée des fronts d'onde émis par une source ponctuelle au-dessus d'un dioptre, mettant en évidence le phénomène de réfraction. La zone inférieure a un plus grand indice de réfraction et donc une vitesse de phase plus faible que la zone supérieure. Pour une raison de clarté, la réflexion partielle n'est pas montrée.

L'indice de réfraction d'un milieu à une longueur d'onde donnée mesure le facteur de réduction de la vitesse de phase de la lumière dans le milieu. Par exemple, dans un verre ordinaire d'indice 1,5, la vitesse des fronts d'onde vaut 1/1,5=0,67 fois la vitesse dans le vide. Les rayons de lumière changent de direction lorsqu'ils passent d'un matériau à un autre, en suivant les lois de Snell-Descartes, qui mettent en jeu le rapport des indices de réfraction. Cet effet, appelé réfraction, est à la base de la conception des lentilles optiques. Les indices de réfraction se mesurent par réfractométrie.

Sommaire

1 Définition
2 Variations de l'indice de réfraction...
3 Notes et références
4 Voir aussi
- 4.1 Articles connexes
- 4.2 Liens externes

Définition

L'indice de réfraction n d'un milieu déterminé pour une radiation monochromatique donnée est égale au rapport de la vitesse de la lumière c dans le vide, à la vitesse de phase v de cette radiation dans ce milieu :

$n = \frac{c}{v}$

La vitesse de propagation v d'une onde électromagnétique dans un matériau isotrope est reliée à la permittivité diélectrique ε et à la perméabilité magnétique μ par la formule :

εμ v 2 = 1

En particulier, dans le vide, on a :

ε 0 μ 0 c 2 = 1

où $ε 0$ et $μ 0$ sont respectivement la permittivité diélectrique et la perméabilité magnétique du vide.

En conséquence, l'indice de réfraction n est relié aux valeurs relatives $ε r = ε / ε 0$ et $μ r = μ / μ 0$ par la relation :

$n = \sqrt{\varepsilon_r \mu_r}$

Pour un milieu isotrope non magnétique :

$n = \sqrt{\varepsilon_r}$

Ces relations sont également valables pour des valeurs complexes $n + i k$ et $ε r' + i ε r''$ , qui permettent de prendre en compte l'atténuation des ondes dans les milieux absorbants ou métalliques. La partie imaginaire de l'indice est appelée coefficient d'extinction. Il est à noter que dans le cas où on choisit une dépendance temporelle $e i ω t$ au lieu de $e - i ω t$ , l'indice complexe prend la forme $n - i k$ .

Dans le domaine des rayons X, l'indice de réfraction des matériaux devient légèrement inférieur à l'unité. La vitesse de phase du rayonnement est alors supérieure à c. En revanche, la vitesse de groupe reste inférieure à c.

Dans le domaine visible et surtout infrarouge, la permittivité diélectrique relative des métaux est un nombre complexe, proche de l'axe réel négatif. L'indice de réfraction est proche de l'axe imaginaire.

Quelques exemples d'indices de réfraction : 1,33 pour l'eau, aux alentours de 1,5 pour le verre, 2,4 pour le diamant (c'est cet indice élevé qui est en partie responsable de son éclat)

Variations de l'indice de réfraction...

Avec la longueur d'onde

La valeur de l'indice dépend généralement de la longueur d'onde du rayon lumineux utilisé.

La première conséquence est l'effet sur la réfraction : l'angle de réfraction n'est pas le même pour différentes « couleurs ». Ceci explique la décomposition de la lumière par un prisme ou par des gouttes d'eau (arc-en-ciel). Ce phénomène est aussi responsable des aberrations chromatiques dans les instruments d'optique.

Les indices de réfraction doivent donc se référer à une radiation monochromatique précise : la raie D de l'hélium (longueur d'onde 587,6 nm), proche du milieu du spectre visible, est utilisée fréquemment comme référence. On utilise également la raie D du sodium (longueur d'onde 589 nm). Il faut donc faire attention puisque toutes les deux ont tendance à être représentées par l'indice « $n D$ », mais puisque les valeurs des deux longueurs d'ondes sont très près l'une de l'autre, les indices sont généralement équivalents dans les deux cas, compte tenu de l'arrondissement des décimales et des incertitudes liées aux instruments de mesures.

La variation de l'indice de réfraction d'un milieu transparent dans le spectre visible est appelée dispersion ; elle est caractérisée par le coefficient de dispersion ou nombre d'Abbe :

$\nu = \frac{n_D - 1}{n_F - n_C}$

F et C désignant deux raies de l'hydrogène (longueurs d'onde $λ F$ = 486,1 nm et $λ C$ = 656,3 nm)

Pour la radiation D, l'indice absolu $n D$ de l'eau à 20 °C est de 1,333 ; celui d'un verre ordinaire est compris entre 1,511 à 1,535.

Pour la lumière visible, une approximation satisfaisante des variations de l'indice avec la longueur d'onde est donné par la Loi de Cauchy^[1]

$n_{\lambda} = a_0 + \frac{a_1}{\lambda^2}$

où $a 0$ et $a 1$ sont des coefficients positifs, $a 0$ sans dimension, $a 1$ en m², à préciser pour chaque milieu.

Une généralisation de cette équation est l'équation de Sellmeier

$n^2(\lambda) = 1 + \frac{B_1 \lambda^2 }{ \lambda^2 - C_1} + \frac{B_2 \lambda^2 }{ \lambda^2 - C_2} + \frac{B_3 \lambda^2 }{ \lambda^2 - C_3}$

où B_1,2,3 et C_1,2,3 sont les coefficients de Sellmeier déterminés expérimentalement. Ces coefficients sont généralement déterminés pour λ mesuré en microns. λ est la longueur d'onde dans le vide et non pas celle dans le milieu d'intérêt, qui est λ/n(λ).

Variations de l'indice de quelques matériaux en fonction de la longueur d'onde

**Indices de réfraction**^[2]
Longueur d'onde (nm)	Source	BK7	SF2	Silice UV	CaF₂	MgF₂ (n_O)	MgF₂ (n_e)	Quartz cristallin (n_O)	Quartz cristallin (n_e)
193	Laser excimère ArF	1,65528	1,52127	1,57077	1,50153	1,42767	1,44127	1,66091	1,67455
244	Laser excimère ArF	1,58265	1,98102	1,51086	1,46957	1,40447	1,41735	1,60439	1,61562
248	Laser excimère ArF	1,57957	1,93639	1,50855	1,46803	1,40334	1,41618	1,60175	1,61289
257	Laser à l'argon ionisé	1,57336	1,86967	1,50383	1,46488	1,40102	1,41377	1,59637	1,60731
266	Laser à Nd:YAG	1,56796	1,82737	1,49968	1,46209	1,39896	1,41164	1,59164	1,60242
308	Laser excimère XeCl	1,55006	1,73604	1,48564	1,45255	1,39188	1,40429	1,57556	1,58577
325	Laser HeCd	1,54505	1,71771	1,48164	1,44981	1,38983	1,40216	1,57097	1,58102
337,1	Laser N₂	1,54202	1,70749	1,47919	1,44813	1,38858	1,40085	1,56817	1,57812
351	Laser excimère XeF	1,53896	1,69778	1,47672	1,44642	1,38730	1,39952	1,56533	1,57518
351,1	Laser à l'argon ionisé	1,53894	1,69771	1,47671	1,44641	1,38729	1,39951	1,56531	1,57516
354,7	Laser Nd:YAG	1,53821	1,69548	1,47612	1,44601	1,38699	1,39920	1,56463	1,57446
363,8	Laser à l'argon ionisé	1,53649	1,69029	1,47472	1,44504	1,38626	1,39844	1,56302	1,57279
404,7	Arc au mercure, raie h	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
416	Laser au kripton ionisé	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
435,8	Arc au mercure, raie g	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
441,6	Laser HeCd	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
457,9	Laser à l'argon ionisé	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
465,8	Laser à l'argon ionisé	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
472,7	Laser à l'argon ionisé	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
476,5	Laser à l'argon ionisé	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
480	Arc au cadmium, raie F'	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
486,1	Arc à l'hydrogène, raie F	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
488	Laser à l'argon ionisé	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
496,5	Laser à l'argon ionisé	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
501,7	Laser à l'argon ionisé	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
510,6	Laser à vapeur de Cu	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
514,5	Laser à l'argon ionisé	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
532	Laser Nd:YAG	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
543,5	Laser HeNe	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
546,1	Arc au mercure, raie e	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
578,2	Laser à vapeur de Cu	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
587,6	Arc à l'hélium, raie d	1,51680	1,x	1,x	1,x	1,x	1,x	1,x	1,x
589,3	Arc au sodium, raie D	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
594,1	Laser HeNe	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
611,9	Laser HeNe	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
628	Laser rubis	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
632,8	Laser HeNe	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
635	Diode laser	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
643,8	Arc au cadmium, raie C'	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
647,1	Laser au kripton ionisé	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
650	Diode laser	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
656,3	Arc à l'hydrogène, raie C	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
670	Diode laser	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
676,4	Laser au kripton ionisé	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
694,3	Laser rubis	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
750	Diode laser	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
780	Diode laser	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
830	Diode laser	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
850	Diode laser	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
852,1	Arc au césium, raie s	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
905	Diode laser	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
980	Diode laser	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
1014	Arc au mercure, raie t	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
1053	Laser Nd:YLF	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
1060	Laser Nd:verre	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
1064	Laser Nd:YLF	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
1300	Diode laser	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
1320	Laser Nd:YLF	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
1550	Diode laser	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
1970.1	Arc au mercure	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
2100	Laser Ho:YAG	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
1325,4	Arc au mercure	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x
2940	Laser Er:YAG	1,x	1,x	1,x	1,x	1,x	1,x	1,x	1,x

Avec la température et la pression

L'indice d'un milieu dépend des paramètres qui caractérisent le milieu : température, pression, densité, etc. Les contraintes imposées à un matériau transparent modifient également son indice. La conséquence de cette contrainte est généralement l'apparition d'une biréfringence liée à l'anisotropie qui en résulte. Ceci est utilisé pour étudier certaines structures mécaniques.

Cas de l'atmosphère terrestre

Suréfraction d'un faisceau radar

L’indice de l'air est égal à 1,000 292 6 dans les conditions normales de température et de pression dans l’atmosphère terrestre, mais cet indice dépend de la masse volumique de l'air, et sa variation continue entre des couches de température différente. On définit $\triangle n$ comme le co-indice N qui s'exprime ainsi $N = (n - 1) * 10 6$ . N est relié aux paramètres d'environnement par la formule^[3] :

$N=77,6 \left( \frac {P} {T} \right) + 3,73*10^5 \left( \frac {e}{T^2} \right)\begin{cases} P = pression\ exprim\acute{e}e\ en\ hPa \\ T = temp \acute{e} rature \ absolue\ (K)\\ e = pression\ de\ vapeur\ d'eau\ contenue\ dans\ l'air\ (hPa) \end{cases}$

On peut donc mesurer la variation de N quand on connait P, e et T; et vice-versa.

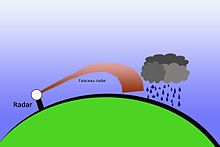
Le principe affecte la propagation de toutes les ondes qui parcourront un chemin différent de la ligne droite en traversant les couches de l'atmosphère. Il permet d'expliquer les mirages dans le domaine de la lumière visible et dans le domaine des radars, les échos de sol se développant lors d'une inversion de température^[3].

Avec la direction de propagation : la biréfringence

Certains matériaux n'ont pas un indice de réfraction isotrope : il dépend alors de la direction de propagation et l'état de polarisation de la lumière. Cette propriété porte le nom de biréfringence.

Article détaillé : Biréfringence.

Notes et références

↑ Réfraction, Comprendre la météo, Météo-France. Consulté le 2010-09-29
↑ Catalogue Général 2006-2007 - Newport, pages 492-493
↑ ^{a et b} (en)Fabry, F., C. Frush, I. Zawadzki et A. Kilambi, « Extracting near-surface Index of refraction using radar phase measurements from ground targets », dans Journal of Atmospheric and Oceanic Technology, American Meteorological Society, n^o 14, 1997, p. 978-987 [texte intégral]

Voir aussi

Liens externes

Portail de la physique

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Indice de réfraction de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Indice De Réfraction — Image animée des fronts d onde émis par une source ponctuelle au dessus d un dioptre, mettant en évidence le phénomène de réfraction. La zone inférieure a un plus grand indice de réfraction et donc une vitesse de phase plus faible que la zone… … Wikipédia en Français
Indice de refraction — Indice de réfraction Image animée des fronts d onde émis par une source ponctuelle au dessus d un dioptre, mettant en évidence le phénomène de réfraction. La zone inférieure a un plus grand indice de réfraction et donc une vitesse de phase plus… … Wikipédia en Français
indice de réfraction — lūžio rodiklis statusas T sritis automatika atitikmenys: angl. index of refraction; refraction index; refractive index vok. Brechungsindex, m; Brechungsverhältnis, n; Brechungszahl, f; Brechzahl, f; Refraktionsindex, m rus. индекс преломления, m; … Automatikos terminų žodynas
indice de réfraction — lūžio rodiklis statusas T sritis Standartizacija ir metrologija apibrėžtis Esant nesugeriančiai terpei, tai elektromagnetinės spinduliuotės sklidimo greičio vakuume ir tam tikro dažnio elektromagnetinės spinduliuotės fazinio greičio terpėje… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
indice de réfraction — lūžio rodiklis statusas T sritis Standartizacija ir metrologija apibrėžtis Medžiagos parametras, apibūdinantis jos savybę laužti šviesos bangas. atitikmenys: angl. refraction index; refractive index vok. Brechungsindex, m rus. показатель… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
indice de réfraction — lūžio rodiklis statusas T sritis fizika atitikmenys: angl. refraction index; refractive index vok. Brechungsindex, m; Brechungsverhältnis, n; Brechungszahl, f rus. показатель преломления, m pranc. indice de réfraction, m … Fizikos terminų žodynas
indice de réfraction — lūžio rodiklis statusas T sritis Energetika apibrėžtis Vakuumo ir tam tikros aplinkos šviesos greičių santykis. atitikmenys: angl. refraction index vok. Brechungsindex, m rus. показатель преломления, m pranc. indice de réfraction, m … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
Indice de refraction des microbilles de verre pour marquages routiers — Indice de réfraction des microbilles de verre pour marquages routiers L indice de réfraction des microbilles de verre pour marquages routiers, microbilles de verre à la base de la visibilité nocturne, est une des propriétés de ces microbilles qui … Wikipédia en Français
Indice de réfraction absolu — ● Indice de réfraction absolu indice d un milieu par rapport au vide … Encyclopédie Universelle
Indice de réfraction du second milieu par rapport au premier — ● Indice de réfraction du second milieu par rapport au premier rapport de la vitesse de la lumière dans le premier milieu à la vitesse de la lumière dans le second … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Indice de réfraction

Sommaire

Définition