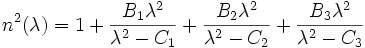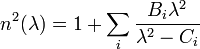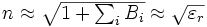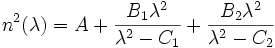Equation de Sellmeier

Equation de Sellmeier

Équation de Sellmeier

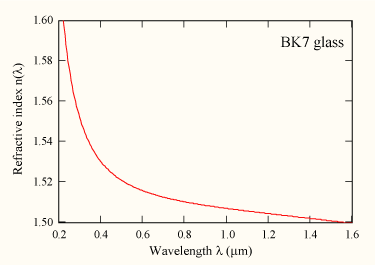Un graphique de l'indice de réfraction en fonction de la longueur d'onde en utilisant l'équation de Sellmeier pour du verre BK7.

En optique, l'équation de Sellmeier est une relation empirique entre l'indice de réfraction n et la longueur d'onde λ pour un milieu transparent donné. La forme habituelle de cette équation pour les verres est[1]:

n^2(\lambda) = 1 + \frac{B_1 \lambda^2 }{ \lambda^2 - C_1} + \frac{B_2 \lambda^2 }{ \lambda^2 - C_2} + \frac{B_3 \lambda^2 }{ \lambda^2 - C_3}

où B1,2,3 et C1,2,3 sont les coefficients de Sellmeier déterminés expérimentalement. Ces coefficients sont généralement déterminés pour λ mesuré en microns. λ est la longueur d'onde dans le vide et non pas celle dans le milieu d'intérêt, qui est λ/n(λ).

Cette équation est utilisée pour déterminer la dispersion de la lumière dans un milieu réfringent. Une différente forme de l'équation est parfois utilisée pour certains types de matériaux, par exemple les cristaux.

Cette équation a été trouvée en 1871 par W. Sellmeier, et était un développement du travail de Augustin Cauchy sur l'équation de Cauchy pour modéliser la dispersion.

Les coefficients de Sellmeier pour plusieurs verres optiques communs peuvent êtres trouvés dans le catalogue de Schott[2]. Dans sa forme la plus générale, l'équation de Sellmeier est:

n^2(\lambda) = 1 + \sum_i \frac{B_i \lambda^2}{\lambda^2 - C_i}

où chaque terme de la somme représente une résonance d'absorption de force Bi à la longueur d'onde √Ci. Par exemple, les coefficients pour le BK7 ci-dessous correspondent à deux résonance d'absorption dans l'ultraviolet, est une dans l'infrarouge. Près de chaque pic d'absorption, l'équation donne la valeur non-physique de n=±∞, et un modèle de dispersion plus précis, tel que le modèle de dispersion d'Helmoltz, est requis pour décrire adéquatement ces régions.

Aux longues longueurs d'ondes loin des pics d'absorption, la valeur de n tend vers :

\begin{matrix} n \approx \sqrt{1 + \sum_i B_i } \approx \sqrt{\varepsilon_r} \end{matrix}

où εr est la constante diélectrique relative du milieu.

L'équation de Sellmeier peut également prendre la forme :

n^2(\lambda) = A + \frac{B_1 \lambda^2}{\lambda^2 - C_1} + \frac{ B_2 \lambda^2}{\lambda^2 - C_2}

où le coefficient A est une approximation de la contribution de l'absorption des courtes longueurs d'ondes (par exemple, ultraviolet) à l'indice de réfraction dans les longueurs d'ondes plus grandes.

Table de coefficients de l'équation de Sellmeier
Matériau B1 B2 B3 C1 C2 C3
Al2O3
Alumine
(pour l'onde ordinaire)		 1.43134930 6.5054713x10−1 5.3414021 5.2799261x10−3µm2 1.42382647x10−2µm2 3.25017834x102µm2
Al2O3
Alumine
(pour l'onde extraordinaire)		 1.5039759 5.5069141x10−1 6.5937379 5.48041129x10−3µm2 1.47994281x10−2µm2 4.0289514x102µm2
BK7 1.03961212 2.31792344x10−1 1.01046945 6.00069867x10−3µm2 2.00179144x10−2µm2 1.03560653x102µm2

Sommaire

Notes et références de l'article

Voir aussi

Articles connexes

Liens et documents externes

Ce document provient de « %C3%89quation de Sellmeier ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Equation de Sellmeier de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Équation de sellmeier — Un graphique de l indice de réfraction en fonction de la longueur d onde en utilisant l équation de Sellmeier pour du verre BK7. En optique, l équation de Sellmeier est une relation empirique entre l indice de réfraction n et la longueur d onde λ …   Wikipédia en Français

  • Équation de Sellmeier — Un graphique de l indice de réfraction en fonction de la longueur d onde en utilisant l équation de Sellmeier pour du verre BK7. En optique, l équation de Sellmeier est une relation empirique entre l indice de réfraction n et la longueur d onde λ …   Wikipédia en Français

  • Sellmeier equation — In optics, the Sellmeier equation is an empirical relationship between refractive index n and wavelength λ for a particular transparent medium. The usual form of the equation for glasses [ [http://schott.com/optics devices/english/download/tie 29 …   Wikipedia

  • Cauchy's equation — is an empirical relationship between the refractive index n and wavelength of light λ for a particular transparent material. It is named for the mathematician Augustin Louis Cauchy, who defined it in 1836.The most general form of Cauchy s… …   Wikipedia

  • Liste Des Équations Et Formules — Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X …   Wikipédia en Français

  • Liste des equations et formules — Liste des équations et formules Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H …   Wikipédia en Français

  • Liste des équations et formules — Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X …   Wikipédia en Français

  • Liste d'équations et formules — Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X …   Wikipédia en Français

  • Indice de réfraction — Image animée des fronts d onde émis par une source ponctuelle au dessus d un dioptre, mettant en évidence le phénomène de réfraction. La zone inférieure a un plus grand indice de réfraction et donc une vitesse de phase plus faible que la zone… …   Wikipédia en Français

  • Triborate de lithium — Général No CAS 12007 41 9 Apparence …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”