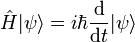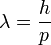Hypothese de De Broglie

Hypothese de De Broglie

Hypothèse de De Broglie

Cet article fait partie de la série
Mécanique quantique
\hat H | \psi\rangle = i\hbar\frac{{\rm d}}{{\rm d}t}|\psi\rangle
Postulats de la mécanique quantique

Histoire de la mécanique quantique

En physique, l'hypothèse de De Broglie est l'affirmation que toute matière est dotée d'une onde associée : ceci donne lieu à la dualité onde-particule. De plus, la longueur d'onde et la quantité de mouvement d'une particule sont reliées par une équation simple :

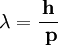\mathbf{ \lambda = { h\over\ p} } qui posait les bases de la mécanique quantique.

Cette hypothèse a été formulée en 1924 par Louis de Broglie dans sa thèse[1] où il argumente son bienfondé et examine ses conséquences. En 1929, il reçoit le prix Nobel [2] pour ces travaux.

Sommaire

Détails

La longueur d'onde et la quantité de mouvement d'une particule sont reliés par l'équation :

\lambda = \frac{h}{p}

où : λ est la longueur d'onde de la particule

h est la constante de Planck de la particule
p est la quantité de mouvement de la particule
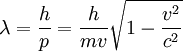
  • Si la particule est de masse non-nulle, cela donne : \lambda = \frac{h}{p} = \frac {h}{{m}{v}} \sqrt{1 - \frac{v^2}{c^2}}
avec : m est la masse de la particule
v est la vitesse de la particule
On remarquera que le cas v = 0 n'est pas envisagé dans cette hypothèse.
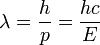
  • Si la particule est de masse nulle (dans le cas du photon par exemple), cela donne : \lambda = \frac{h}{p} = \frac {hc}{E}
avec : p = E / c quantité de mouvement de la particule de masse nulle


Plus l'énergie est grande, plus la fréquence est importante et la longueur d'onde petite.

Si l'on s'intéresse à des particules macroscopiques, la masse des objets mesurés est tellement grande devant la constante de Planck que la longueur d'onde obtenue devient infime (pour une bille, elle serait de l'ordre de 10 − 32 mètres tout au plus). C'est la raison pour laquelle le caractère ondulatoire des objets massifs macroscopiques n'est pas observable.

Les longueurs d'ondes d'objets microscopiques comme l'électron sont de l'ordre de grandeur de la taille des atomes (pour les électrons lents, accélérés sous une différence de potentiel de quelques volts, par exemple). Dans les microscopes électroniques (tension accélératrice de 10 kV), on arrive tout de même à les faire diffracter par des cristaux grâce aux faibles angles d'incidence.

Contexte historique

Article détaillé : Histoire de la mécanique quantique.

Avant

La constante de Planck, introduite en 1900 pour modéliser le rayonnement du corps noir, amena l'idée d'une quantification de l'énergie du champ électromagnétique dépendant de la fréquence de l'onde, ainsi que l'a exprimé clairement Einstein en 1905, alors qu'en théorie et expérimentalement -jusqu'aux expériences de ce début de siècle- l'énergie de cette onde ne semblait dépendre que de son amplitude, comme toutes les ondes connues.
En 1913, Niels Bohr expliqua les raies spectrales de l'atome d'hydrogène, en utilisant de nouveau la quantification, dans son article de juillet 1913 On the Constitution of Atoms and Molecules[3].
Ces théories bien que pertinentes vis-a-vis des données expérimentales, étaient strictement phénoménologiques : il n'existait pas de justification rigoureuse pour la quantification, et ne semblaient pas compatibles avec les autres aspects de la physique classique comme relativiste, malgré les efforts des plus grands physiciens du moment.
Louis de Broglie, nourri d'une connaissance précise de l'histoire de la physique, exprima et argumenta l'idée qui débloqua la situation.

Accueil de l'hypothèse

À la fin de sa soutenance de thèse, Jean Perrin, qui était son directeur de thèse, lui demanda comment mettre en évidence cette onde hypothètique. Louis de Broglie lui répondit, sans hésiter, « en diffractant des électrons ».[réf. nécessaire] Ce qui fut fait en 1927 dans une expérience réalisée par George Paget Thomson, et indépendamment par Clinton Joseph Davisson et Lester Halbert Germer.
Paul Langevin envoya un exemplaire de la thèse à Einstein, qui lui répondit par courrier que Louis de Broglie avait « levé un coin du grand voile ».[4]

Le fait que la thèse ait été soutenue par Einstein amena Erwin Schrödinger à prendre connaissance de l'hypothèse de de Broglie, et en « laissant de côté les conceptions relativistes qui m'avaient initialement guidées, mais serrant de plus près que je ne l'avais fait l'analogie entre mes résultats et la vieille théorie d'Hamilton-Jacobi »[5] obtient en 1925, l'équation différentielle vérifiée par cette onde, l'équation de Schrödinger, non relativiste mais plus maniable que le principe tel que formulé par de Broglie.

Après

Le développement très rapide de la mécanique quantique après la publication de son travail à mis Louis de Broglie face à une interprétation probabiliste de la fonction d'onde qui ne lui convenait pas et, se sentant plus proche de la vision einsteinienne de la physique, il a essayé de développer sa propre interprétation de la théorie quantique : la théorie de l'onde pilote formulée vers 1927.
À noter que ses hypothèses sur les quanta de lumière, évoquées et utilisées dans sa thèse, n'ont pas eu le même succès.

Contenu de la thèse de de Broglie

Cette partie de l'article fait un rapide survol, dans un langage parfois modernisé, du contenu de cette célèbre thèse. Le lecteur soucieux d'exactitude pourra lire la thèse à partir du lien cité en référence.

Une introduction historique

Louis de Broglie dans une première partie examine l'histoire de la physique, mettant en valeur l'émergence de la physique des ondes et de la mécanique. Puis, dans une deuxième partie, il rappelle les étapes de la récente physique des quanta, en particulier les arguments et expériences liés à l'effet photoélectrique et la relation de Planck-Einstein.
Cette introduction fini par ces termes :
« Bref, le moment semblait venu de tenter un effort dans le but d’unifier les points de vue corpusculaire et ondulatoire et d’approfondir un peu le sens véritable des quanta. C’est ce que nous avons fait récemment [6] et la présente thèse a pour principal objet de présenter un exposé plus complet des idées nouvelles que nous avons proposées, des succès auxquels elles nous ont conduit et aussi des très nombreuses lacunes qu’elles contiennent. »

« L'onde de phase »

Après avoir argumenté sur la nécessité d'unifier la théorie de la relativité et la physique des quanta, notamment du fait que les échanges d'énergie se font par quanta dans l'effet photoélectrique, Louis de Broglie écrit :

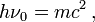
« On peut donc concevoir que par suite d’une grande loi de la Nature, à chaque morceau d’énergie de masse propre m, soit lié un phénomène périodique de fréquence ν0 telle que l’on ait : 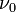\ h\nu_0 = mc^2 \, , \ \nu_0 étant mesurée, bien entendu, dans le système lié au morceau d’énergie. Cette hypothèse est la base de notre système : elle vaut, comme toutes les hypothèses, ce que valent les conséquences qu’on en peut déduire. »

Plus loin dans son travail, il explique ce qui lui fait penser que ce phénomène périodique n'a pas lieu d'être considéré a priori comme confiné : il s'agirait donc d'une onde se propageant dans l'espace.
Louis de Broglie précise alors sa conception de l'atome : « Ce qui caractérise l’électron comme atome d’énergie, ce n’est pas la petite place qu’il occupe dans l’espace, je répète qu’il l’occupe tout entier, c’est le fait qu’il est insécable, non subdivisible, qu’il forme une unité »

Puis, il présente une contradiction apparente entre son hypothèse et la relativité restreinte, disant que c'était là « une difficulté qui [l]’a longtemps intrigué » :

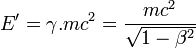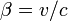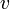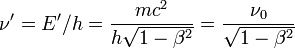  • Un changement de référentiel donne une énergie du corps, dans le nouveau référentiel, égale à E' = \gamma.mc^2 = \frac{mc^2}{\sqrt{1-\beta^2}}, avec \ \beta = v/c où \ v est la vitesse relative des deux référentiels. Donc dans cet autre référentiel, la fréquence du phénomène périodique est égale à \nu' = E'/h = \frac{mc^2}{h \sqrt{1-\beta^2}} = \frac{\nu_0}{\sqrt{1-\beta^2}}.
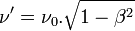  • Ce même changement de référentiel induit, en relativité restreinte, un ralentissement du temps qui donne comme fréquence observée dans le deuxième référentiel : \nu' = \nu_0.\sqrt{1-\beta^2}.

De toute évidence, les deux valeurs de ν' sont incompatibles.

De Broglie en propose la résolution par l'hypothèse qu'on peut considérer l'onde associée au corps comme composée de deux ondes ayant chacune sa fréquence et sa vitesse :

  • La "fréquence de groupe" 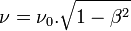\nu = \nu_0.\sqrt{1-\beta^2} et la "vitesse de groupe" 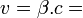\ v = \beta.c = vitesse "de la particule" dans le référentiel. Elles concernent le déplacement des amplitudes de l'onde, on dit aujourd'hui de "l'enveloppe" : cela correspond au déplacement de l'énergie du corps. La vitesse de groupe est celle du corps, inférieure à la vitesse de la lumière.
  • La "fréquence de phase" 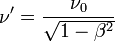\nu' = \frac{\nu_0}{\sqrt{1-\beta^2}} et la "vitesse de phase" 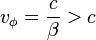\ v_{\phi} = \frac{c}{\beta} > c. Elles concernent le déplacement des crêtes de l'onde postulée, sans que les amplitudes de l'onde ne suivent ce déplacement : il n'y a pas alors de déplacement d'énergie. La vitesse de phase est supérieure à la vitesse de la lumière. C'est la "fréquence de phase", véritable fréquence de l'onde, qui vérifie la relation \ h.\nu' = E.

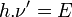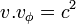La moyenne géométrique des deux vitesses est la vitesse de la lumière : \ v.v_{\phi}=c^2.

Il énonce un théorème qu'il appelle "harmonie des phases". Ce théorème indique que la phase du phénomène périodique ne change pas par changement de référentiel : 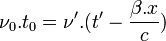\nu_0.t_0 = \nu'.(t'-\frac{\beta.x}{c}). Cette propriété est démontrée de deux manières, dont une utilisant les transformations de Lorentz, et est interprétée comme une indication que l'onde est une onde dans l'espace des phases : c'est une « onde de phase ». De Broglie ne fait aucune hypothèse sur la nature de l'onde.

À la suite de quoi, il étudie des propriétés mathématiques, et aussi physiques dans le cadre de la relativité restreinte, de l'onde de phase.

Principes de moindre action et de Fermat

Après avoir justifié la restriction de son travail au cadre de la relativité restreinte par la difficulté théorique de le concevoir dans le cadre de la relativité générale, Louis de Broglie écrit : « Nous étudierons d’une part le principe mécanique de la moindre action sous ses formes Hamiltonienne et Maupertuisienne dans la dynamique classique et dans celle de la Relativité et d’autre part à un point de vue très général, la propagation des ondes et le principe de Fermat. Nous serons alors amené à concevoir une synthèse de ces deux études, synthèse sur laquelle on peut discuter mais dont l’élégance théorique est incontestable. »


Ainsi, il montre que pour ces deux principes il est possible d'en réécrire la formulation sous une forme très similaire, utilisant la quadri-impulsion du corps (ayant une charge électrique, éventuellement), pour l'un, et le quadri-vecteur d'onde, pour l'autre principe. Remarquant ensuite que l'égalité hν = E = γ.mc2 est l'égalité de la première coordonnée de ces deux quadri-vecteurs (plus exactement leur proportionnalité par la constante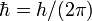 \hbar = h/(2\pi) car k0 = ω = 2π.ν et p0 = E = γ.mc2), de Broglie écrit : « Le fait que deux vecteurs aient une composante égale ne prouve pas qu’il en soit de même pour les autres. Cependant, par une généralisation tout indiquée nous poserons » l'égalité des autres coordonnées (leur proportionnalité par la même constante) : 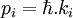p_i = \hbar.k_i pour i = 0;1;2;3.

De Broglie conclut : « Le principe de Fermat appliqué à l’onde de phase est identique au principe de Maupertuis appliqué au mobile ; les trajectoires dynamiquement possibles du mobile sont identiques aux rayons possibles de l’onde. »

Puis il utilise ces nouvelles égalités dans des exemples simples afin de mieux montrer leur signification.

Etude du modèle quantique de l'atome

Louis de Broglie rappelle le modèle de l'atome d'hydrogène avancé par Niels Bohr, permettant de calculer les orbites stables de l'électron autour du proton. L'énoncé en a été amélioré par Arnold Sommerfeld et Wilson, puis Einstein en 1917 « a donné à la condition de quantification une forme invariante par rapport aux changements de coordonnées » utilisant l'intégrale du principe de moindre action telle qu'avancée plus haut dans la thèse. Utilisant alors l'égalité supposée avec le principe de Fermat pour l'onde de phase de l'électron, de Broglie montre que les orbites stables sont celles dont la longueur l vérifie l = n.λ, où λ = la longueur d'onde de l'onde de phase et 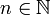n \in \N pour qu'il y ai résonance, et retrouve ainsi la formule de Bohr.
Puis, il discute du caractère approximatif de ces conditions mathématiques par rapport à la réalité physique où interviennent la dimension de l'électron et le temps de libration nécessaire à la stabilisation de l'orbite.
Enfin, il traite l'ensemble proton-électron vis-à-vis de leur centre de gravité et examine alors la géométrie des orbites, à l'aide de leurs ondes de phase.

Les quanta de lumière

Louis de Broglie développe sa conception de la lumière basée sur la théorie des quanta, la relativité restreinte et son onde de phase. Il élabore une vision des quanta de lumière comme dotés d'une masse non-nulle en invoquant l'équivalence masse-énergie de la relativité restreinte (m = E / c2). Ayant une masse non nulle, mais expérimentalement inférieure à 10-44 gramme, un photon ne peut donc pas atteindre la "vitesse de la lumière" (rebaptisée "vitesse limite de l'énergie"). Admettant que « c’est un fait expérimental que l’énergie lumineuse se déplace avec une vitesse indiscernable de la valeur limite c », Louis de Broglie émet l'hypothèse « qu’un jour en mesurant la vitesse dans le vide d’ondes de très basse fréquence, on trouvera des nombres assez sensiblement inférieurs à c ».

Louis de Broglie évoque la diffraction, sans proposer une synthèse mathématique précise entre les points de vues corpusculaire et ondulatoire.
Il utilise les quanta de lumière associés à son onde de phase (notamment l'idée qu'ils vont à une vitesse inférieure à la vitesse limite de l'énergie), dans les cas d'un effet Doppler par mouvement de la source, de la réflexion sur un miroir mobile, et au sujet de la pression de radiation du rayonnement noir : il retouve les formules des intensités lumineuses « connus des théories ondulatoires ».

Abordant l'étude de « l’optique ondulatoire », il écrit que « malheureusement, il est encore impossible d’arriver à des résultats satisfaisants » par la théorie des quanta, comparativement à la théorie de Maxwell. Louis de Broglie fait des propositions théoriques qui « doivent être considérées comme de vagues suggestions plutôt que comme de véritables explications », entre autres : « assimiler les ondes de phase aux ondes électromagnétiques, tout au moins quant à la répartition des phases dans l’espace, la question des intensités devant être réservée », « la probabilité des réactions entre atomes de matière et atomes de lumière est en chaque point liée à la résultante (ou plutôt à la valeur moyenne de celle-ci) d’un des vecteurs caractérisant l’onde de phase », le « postulat » que « l’onde de phase liée au mouvement d’un atome de lumière peut en passant sur des atomes matériels excités, déclencher l’émission d’autres atomes de lumière dont la phase sera en accord avec celle de l’onde » et exprime l'accord entre sa conception de la lumière et « loi des fréquences de Bohr : h.ν = W1 − W2. »

La diffusion des rayons X

De Broglie désire « étudier la diffusion des rayons X et γ, et montrer sur cet exemple particulièrement suggestif la position respective actuelle de la théorie électromagnétique et de celle des quanta de lumière »
Il commence « par définir le phénomène même de la diffusion : lorsqu’on envoie un faisceau de rayons sur un morceau de matière, une partie de l’énergie en est, en général, éparpillée dans toutes les directions. On dit qu’il y a diffusion et affaiblissement par diffusion du faisceau pendant la traversée de la substance. »
Puis il passe en revue les diverses lois de la diffusion de la lumière et surtout des rayons X :

  • La « théorie électronique », dont de Broglie note qu'elle « semble en opposition directe avec le modèle atomique de Bohr », permet de conclure que dans le domaine du visible, « la radiation secondaire globale est en raison inverse de la 4ème puissance de la longueur d’onde ; les radiations sont donc d’autant plus diffusées qu’elles sont de fréquence plus élevées. C’est sur cette conclusion que lord Rayleigh a appuyé sa belle théorie de la couleur bleue du ciel ». Et « dans le domaine des très hautes fréquences (Rayons X et γ) », « M. J. J. Thomson (...) constitua la première théorie de la diffusion des Rayons X. » en concluant, entre autres, que « l’énergie diffusée varie en fonction de θ comme (1 + cosθ) / 2 », où θ est « l’angle du prolongement de la direction d’incidence avec la direction de diffusion ».
  • La « théorie de M. Debye » mise au point car la théorie précédente n'est pas cohérentes avec les résultats de certaines expériences de MM. Bragg et Barkia.
  • La « théorie récente de MM. P. Debye et A. H. Compton » dont la mise au point fût rendue nécessaire car « les expériences dans le domaine des rayons X durs et des rayons γ ont révelé des faits très différents de ceux que les théories précédentes peuvent prévoir. ». Après un rapide exposé de cette théorie utilisant le quanta de lumière et la quantité de mouvement, Louis de Broglie note que « dans un article de la Physical Review, de mai 1923, et dans un plus récent article du Philosophical Magasine (novembre 1923), M. A.-H. Compton a montré que les nouvelles idées ci-dessus exposées rendaient compte de beaucoup de faits expérimentaux et qu’en particulier pour les rayons durs et les corps légers, la variation de longueur d’onde prévue était quantitativement vérifiée. ». Toutefois, « pour les basses fréquences », de Broglie rappelle qu'une expérience de M. Ross montre « l’existence d’une raie non déplacée » non expliquée par cette théorie, et cite d'autres résultats expérimentaux liés à la « loi empirique due à MM. Bragg et Pierce ».

Puis Louis de Broglie annonce « on peut généraliser la théorie de Compton-Debye en considérant la diffusion d’un quantum de radiation par un électron en mouvement. », et, tenant compte de la fréquence de l'onde de phase pour le quanta de lumière, trouve une loi de diffusion incluant la loi de Compton et un effet Doppler, concluant qu'il « n’est pas impossible que certaines des conclusions ci-dessus énoncées puissent être soumises à une vérification expérimentale ».

La mécanique statistique et les quanta

Louis de Broglie rappelle « une démonstration bien connue de l’expression analytique des grandeurs thermodynamiques, démonstration qui a l’avantage d’être valable aussi bien quand la suite des états possibles est discontinue que dans le cas inverse », soulignant que « le théorème de Liouville (valable également dans la dynamique de la relativité) nous apprend que l’élément d’extension en phase d’une molécule égale à dxdydzdpdqdr (où x, y et z sont les coordonnées, p, q, r les moments correspondants) est un invariant des équations du mouvement dont la valeur est indépendante du choix des coordonnées », puis admettant « que le nombre des états d’égale probabilité représentés par un élément de cette extension en phase était proportionnel à la grandeur de celui-ci », « ceci conduit immédiatement à la loi de répartition de Maxwell ». Louis de Broglie rappelle ensuite que M. Planck a énoncé « l’hypothèse suivante quelque peu déconcertante : L’extension en phase d’une molécule est divisée en cellules d’égale probabilité dont la valeur est finie et égale à h3 » pour aboutir aux égalités donnant l'énergie et l'entropie du système thermodynamique en fonction de ses caractéristiques.

Puis Louis de Broglie reprend la démonstration en y introduisant les ondes de phase « formant des systèmes stationnaires (c’est-à-dire résonant sur les dimensions de l’enceinte) », « comme dans la conception du rayonnement noir développée par M. Jeans », ce qui est possible car « pendant la durée du libre parcours [d'un atome dans son environnement], l’onde de phase peut parcourir plusieurs fois la longueur d’un récipient même de grande dimension » du fait que sa très grande vitesse (supérieure à la vitesse limite de l'énergie). Démontrant l'égalité λ = h / (mv), utilisant les vitesses de phase et de groupe, Louis de Broglie fait aboutir ses calculs à une formulation du « nombre [d'atomes] qui sont contenus dans l’élément de volume dxdydz et dont l’énergie cinétique est comprise entre w et w+dw » qui lui permet d'écrire « Nous justifions donc l’hypothèse de M. Planck et, par suite, les résultats obtenus par ce savant et exposés plus haut ».

Louis de Broglie cherche ensuite à appliquer ces résultats à un « gaz d'atomes de lumières », mais conclut cet essai par ces mots : « Malheureusement, la loi ainsi obtenue est la loi de Wien qui est seulement le premier terme de la série qui constitue la loi expérimentalement exacte de Planck. Ceci ne doit pas nous surprendre car, en supposant les mouvements des atomes de lumière complètement indépendants, nous devons nécessairement parvenir à une loi dont le facteur exponentiel est identique à celui de la loi de Maxwell. »
Louis de Broglie poursuit : « Pour retrouver le résultat de Planck, il faudra donc faire ici une nouvelle hypothèse (...) sans nous éloigner de la conception des quanta de lumière », à savoir « Si deux ou plusieurs atomes ont des ondes de phase qui se superposent exactement dont on peut dire par suite qu’ils sont transportés par la même onde, leurs mouvements ne pourront plus être considérés comme entièrement indépendants et ces atomes ne pourront plus être traités comme des unités distinctes dans les calculs de probabilité ». « Cette hypothèse de cohérence nous oblige à reprendre entièrement la démonstration de la loi de Maxwell. Comme nous ne pouvons plus prendre chaque atome comme « objet » de la théorie générale, ce sont les ondes de phase stationnaires élémentaires qui doivent jouer ce rôle » écrit de Broglie, avant d'aboutir à la forme de Planck après de quelques calculs utilisant cette hypothèse.
Puis, de Broglie retrouve la loi de Planck des « fluctuations d’énergie dans un volume V de rayonnement noir », ce qui lui permet de conclure « on peut également évaluer correctement les fluctuations du rayonnement noir en ne faisant aucunement appel à la théorie des interférences, mais en introduisant la cohérence des atomes liés à une même onde de phase ».

Appendice sur les quanta de lumière

Dans cet appendice, Louis de Broglie revient sur la conception des « atomes de lumière comme de petits centres d’énergie caractérisés par une masse propre très faible m0 et animés de vitesse généralement très voisines de c, de telle façon qu’il existe entre la fréquence ν, la masse propre m0 et la vitesse 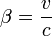\beta = \frac{v}{c} la relation : » 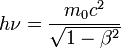h \nu = \frac{m_0c^2}{\sqrt{1- \beta ^2}}, ce qui amenant 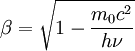\beta = \sqrt{1-\frac{m_0c^2}{h \nu}} donne une vitesse nulle, voir imaginaire suivant les valeurs de la fréquence ν.
Pour lever cette objection, Louis de Broglie rappelle le succès dans la présente thèse en « concevant l’existence d’ensembles d’atomes de lumière liés à la propagation d’une même onde de phase », et poursuit, plus loin, «  nous pourrions peut-être supposer que la masse des centres d’énergie liés à une même onde diffère de la masse propre m0 d’un centre isolé et dépend du nombre d’autres centres avec lesquels ils se trouvent en interaction. On aurait alors : μ0 = f(p) avec , f(1) = m0 en désignant par p le nombre des centres portés par l’onde », ce qui lui permet de conclure que « La vitesse de l’ensemble des p centres formant une onde serait alors : »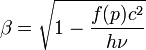 \beta = \sqrt{1-\frac{f(p)c^2}{h \nu}} , avec quelques propriétés supplémentaire sur la fonction f permettant de lever l'objection.
« L’hypothèse précédente détruit un peu la simplicité de la conception du « quantum de lumière », mais cette simplicité ne peut certainement pas être entièrement conservée si l’on veut pouvoir raccorder la théorie électromagnétique avec la discontinuité révélée par les phénomènes photoélectriques. » écrit de Broglie, avant de conclure « Il faut avouer que la structure réelle de l’énergie lumineuse reste encore très mystérieuse. »

Conclusion

Après avoir rappelé les différents points qu'il a développés dans sa thèse, et appelant de ses vœux « une théorie électromagnétique nouvelle conforme naturellement au principe de Relativité, rendant compte de la structure discontinue de l’énergie radiante et de la nature physique des ondes de phase », Louis de Broglie conclut : « La présente théorie doit donc plutôt être considérée comme une forme dont le contenu physique n’est pas entièrement précisé que comme une doctrine homogène définitivement constituée. »

Articles connexes

Références

  1. ↑ (fr) thèse de 1924,
  2. ↑ (en)Broglie, Louis de, The wave nature of the electron, Nobel Lecture, December 12, 1929
  3. ↑ En francais : sur la constitution des atomes et molécules.
  4. ↑ Einstein à Langevin. 16 décembre 1924. Einstein Archive, Jerusalem
  5. ↑ Le dualisme des ondes et corpuscules dans l'oeuvre d'Albert Einstein. L. de Broglie, 1955
  6. ↑ (fr)note de 1923, présentée par Jean Perrin
  • Portail de la physique Portail de la physique
Ce document provient de « Hypoth%C3%A8se de De Broglie ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Hypothese de De Broglie de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Hypothèse De De Broglie — Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire …   Wikipédia en Français

  • Hypothèse de De Broglie — Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire …   Wikipédia en Français

  • Hypothèse de de broglie — Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire …   Wikipédia en Français

  • Hypothèse de de Broglie — « Longueur d onde de de Broglie » redirige ici. Pour le concept statistique, voir Longueur d onde thermique de de Broglie. En physique, l hypothèse de de Broglie est l affirmation que toute matière est dotée d une onde associée :… …   Wikipédia en Français

  • Hypothese von de Broglie — de Broilio hipotezė statusas T sritis fizika atitikmenys: angl. de Broglie’s hypothesis vok. Hypothese von de Broglie, f rus. гипотеза де Бройля, f pranc. hypothèse de de Broglie, f …   Fizikos terminų žodynas

  • hypothèse de de Broglie — de Broilio hipotezė statusas T sritis fizika atitikmenys: angl. de Broglie’s hypothesis vok. Hypothese von de Broglie, f rus. гипотеза де Бройля, f pranc. hypothèse de de Broglie, f …   Fizikos terminų žodynas

  • BROGLIE (L. de) — Prix Nobel de physique (1929) pour la «découverte de la nature ondulatoire de l’électron», Louis de Broglie a réussi la paradoxale synthèse consistant à étendre aux particules matérielles le dualisme onde corpuscule, valable dans les théories de… …   Encyclopédie Universelle

  • Relation de De Broglie — Hypothèse de De Broglie Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire …   Wikipédia en Français

  • Louis de Broglie — Pour les autres membres de la famille, voir : Maison de Broglie. Louis Victor de Broglie Naissance 15 août …   Wikipédia en Français

  • Louis-Victor de Broglie — Louis de Broglie Louis Victor de Broglie Naissance 15 août 1892 Dieppe (France) Décès 19  …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”