- Groupe de lie compact
-
Groupe de Lie compact
Un groupe de Lie compact est un groupe de Lie réel ou complexe dont l'espace topologique sous-jecent est compact. Un groupe de Lie réel compact admet une métrique riemannienne invariante par translations à droite et à gauche. La classification des groupes de Lie complexes compacts est connue : ils sont tous commutatifs.
Sommaire
Groupe de Lie réel compact
Représentation d'un groupe de Lie compact
Article détaillé : Représentation d'un groupe de Lie compact.Un groupe de Lie réel compact G est un exemple de groupe topologique compact. En tant que tel, il admet une unique mesure de probabilité invariante par translation à gauche, appelée la mesure de Haar de G. Toute représentation du groupe G de dimension finie est équivalente à une représentation unitaire. Plus exactement, pour tout espace vectoriel réel ou complexe V et tout morphisme de groupes de Lie
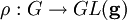, il existe une structure euclidienne et hermitienne sur V invariante par l'action de G : l'application ρ est à valeurs dans les groupe orthogonal ou groupe unitaire associés.Métrique riemannienne biinvariante
Pour tout groupe de Lie réel connexe G, toute structure euclienne sur l'espace tangent
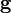de G en l'élément neutre induit par transport des structures une unique métrique riemannienne sur G invariante par translation à gauche. Si le groupe n'est pas commutatif, cette métrique n'a aucune raison d'être invariante par translation à droite.Si mg et dg sont les multiplications à gauche et à droite par g et par g-1 ; par définition, la différentielle en l'élément neutre de mgdg est ad(g). Via la correspondance précédente, les métriques riemmanniennes biinvariantes sur G correspondent exactement aux structures euclidiennes sur
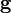invariantes par la représentation adjointe.L'existence d'une structure euclidienne invariante par la représentation adjointe découle précisément des considérations générales sur les représentations.
Pour une telle métrique riemannienne, les multiplications à gauche et à droite sont des isométries riemanniennes. Les sous-groupes à un paramètres sont les géodésiques de G passant par l'élément neutre. Comme G est compact, le théorème de Hopf-Rinow implique l'existence d'une géodésique de l'élément neutre à n'importe quel élément de G. Ainsi :
- L'application exponentielle est surjective.
Groupe de Lie complexe compact
- Un groupe de Lie compact complexe G est commutatif.
La représentation adjointe de G est une application holomorphe
. Comme G est une variété complexe compacte, l'application ad est constante, égale à sa valeur en l'élément neutre. De suite, le crochet de Lie sur son algèbre de Lie est trivial ; et la loi de groupe est commutative.Les groupes de Lie complexes compacts G de dimension 1 sont les quotients de
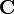par ses réseaux. Un réseau de 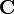est un sous-groupe additif discret de rang 2.
Portail des mathématiques
Catégorie : Groupe de Lie
Wikimedia Foundation. 2010.
