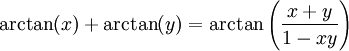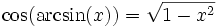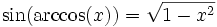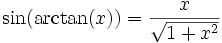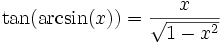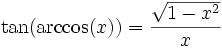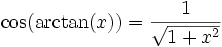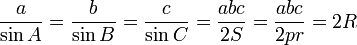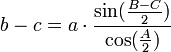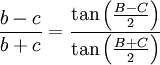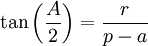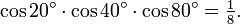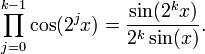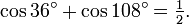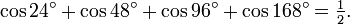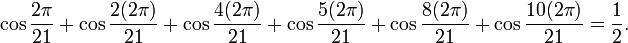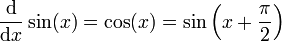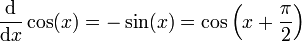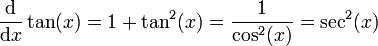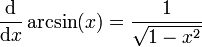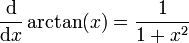- Formule de Simpson
-
Identité trigonométrique
Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une expression comportant des fonctions trigonométriques a besoin d'être simplifiée. Elles constituent donc une « boîte à outils » utile pour la résolution de problèmes.
Les fonctions trigonométriques servent beaucoup en intégration, pour intégrer des fonctions « non trigonométriques » : un procédé habituel consiste à effectuer un changement de variable en utilisant une fonction trigonométrique, et à simplifier ensuite l'intégrale obtenue avec les identités trigonométriques.
Notation : avec les fonctions trigonométriques, nous définirons sin2, cos2, etc., les fonctions telles que pour tout réel x, sin2(x) = (sin(x))2, ...
À partir des définitions
Propriétés liées au cercle trigonométrique
Symétries, parité
Parité - Réflexion d'axe θ = 0 Réflexion d'axe θ = π / 2 Réflexion d'axe θ = π 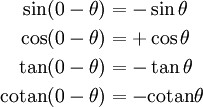
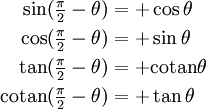
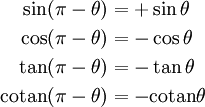
Périodicité, décalages
Décalage de 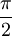
Décalage de π
(Période de tan et cotan)Décalage de 2π
(Période de sin et cos)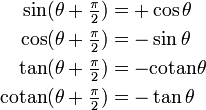
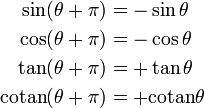
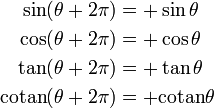
À partir du théorème de Pythagore
Équation trigonométrique
Formules d'addition et de différence
Le moyen le plus rapide pour retrouver ces formules est d'utiliser les formules d'Euler en analyse complexe.
Un moyen mnémotechnique pour retenir : « Le cosinus est méchant : il ne sympathise pas avec les sinus, et de plus il change les signes ».
Une conséquence intéressante de ces égalités est qu'elles permettent de ramener la combinaison linéaire d'un sinus et d'un cosinus à un sinus :
où
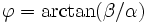 si α est positif et
si α est positif et 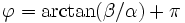 sinon
sinon
Démonstration des formules d'additionIl existe de nombreuses démonstrations possibles dont une utilisant les propriétés d'une corde dans un cercle et une autre la relation entre cosinus d'un angle et produit scalaire. La démonstration proposée ici démontre à la fois la formule du cosinus et celle du sinus. Elle utilise la propriété du changement de repère.
Sur le cercle trigonométrique, on considère le point M tel que
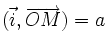 et le point M' tel que la base
et le point M' tel que la base 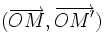 soit orthonormale directe. Les deux vecteurs ont alors, dans la base
soit orthonormale directe. Les deux vecteurs ont alors, dans la base 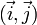 respectivement les coordonnées (cos(a),sin(a)) et ( − sin(a),cos(a))
respectivement les coordonnées (cos(a),sin(a)) et ( − sin(a),cos(a))On considère le point N tel que
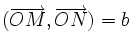 .
.Dans la base
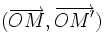 , le vecteur
, le vecteur 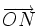 a pour coordonnées (cos(b);sin(b)). Ce qui conduit aux égalités vectorielles :
a pour coordonnées (cos(b);sin(b)). Ce qui conduit aux égalités vectorielles :D'autre part, puisque
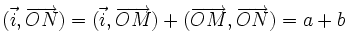 , on a :
, on a :Les formules s'obtiennent alors par identification.
La formule de la tangente s'obtient alors par quotient
par division au numérateur et dénominateur par cos(a)cos(b)
Formules de duplication et d'angle moitié
Formules de l'angle double
Appelées aussi formules d'angle double, elle peuvent être obtenues en remplaçant a et b par x dans les formules d'addition et en utilisant le théorème de Pythagore pour les deux dernières, ou bien en utilisant la formule de Moivre avec n = 2.
Une conséquence amusante de la formule de duplication du cosinus :
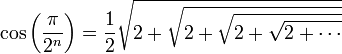 avec n-1 "2" sous le radical.
avec n-1 "2" sous le radical.En passant à la limite, on a une démonstration du fait que
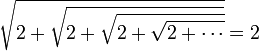
Formules de réduction du carré
Ces formules permettent d'écrire cos2(x), sin2(x) et tan2(x) en fonction du cosinus de l'angle double.
Formules d'angle moitié
En remplaçant x par
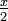 dans les formules de réduction des carrés, et ensuite en cherchant l'expression de
dans les formules de réduction des carrés, et ensuite en cherchant l'expression de 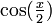 et
et 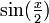 , nous obtenons :
, nous obtenons :En multipliant
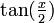 par
par 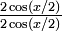 et en le remplaçant par
et en le remplaçant par 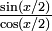 on obtient au numérateur sinx d'après la formule d'angle double, et au dénominateur
on obtient au numérateur sinx d'après la formule d'angle double, et au dénominateur 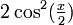 qui est aussi égal à cosx + 1 selon la formule de réduction du carré.
qui est aussi égal à cosx + 1 selon la formule de réduction du carré.La seconde formule vient de la première en multipliant numérateur et dénominateur par sinx et en simplifiant en utilisant le théorème de Pythagore et l'identité remarquable 1 − cos2x = (1 − cosx)(1 + cosx).
Formules impliquant la « tangente de l'arc moitié »
Si on pose
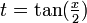 , on a :
, on a :Dans le cas de changement de variable en intégration, on ajoutera :
Ces formules permettent de simplifier des calculs trigonométriques en se ramenant à des calculs sur des fractions rationnelles. Elles permettent aussi de déterminer l'ensemble des points rationnels du cercle unité.
Formules de Simpson
Transformation de produits en sommes
Ces formules peuvent être démontrées en développant leurs membres de droite en utilisant les formules d'addition
Transformation de sommes en produits
Il suffit de remplacer p par
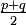 et q par
et q par 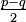 dans les formules de transformation de produit en somme.
dans les formules de transformation de produit en somme.Un moyen mnémotechnique pour retenir : « Si, coco, si ; coco, si si ! Priorité au sinus et à l'addition, −2 à la dernière ».
Formules d'Euler
Article détaillé : Formules d'Euler.Article connexe : Trigonométrie complexe.Formule de Moivre et formules d'angle multiple
La formule de Moivre s'écrit :
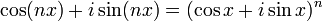 où i est l'unité imaginaire.
où i est l'unité imaginaire.
Si Tn est le n-ième polynôme de Tchebychev alors
Pour tout entier naturel n on a
Le noyau de Dirichlet Dn est la fonction définie par :
- pour tout réel x,
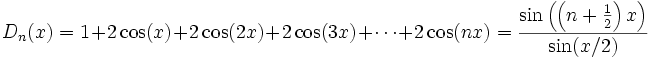
Le produit de convolution de n'importe quelle fonction de carré intégrable et de période 2π avec le noyau de Dirichlet coïncide avec la somme d'ordre n de sa série de Fourier.
Linéarisation
Connaissant la formule de De Moivre :
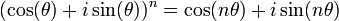 ;
;
il suffit alors de développer la somme grâce à la formule du binôme de Newton, à regrouper les termes sachant que
Formules de linéarisation de degré 2
Formules de Linéarisation de degré 3Formules de Linéarisation : généralisation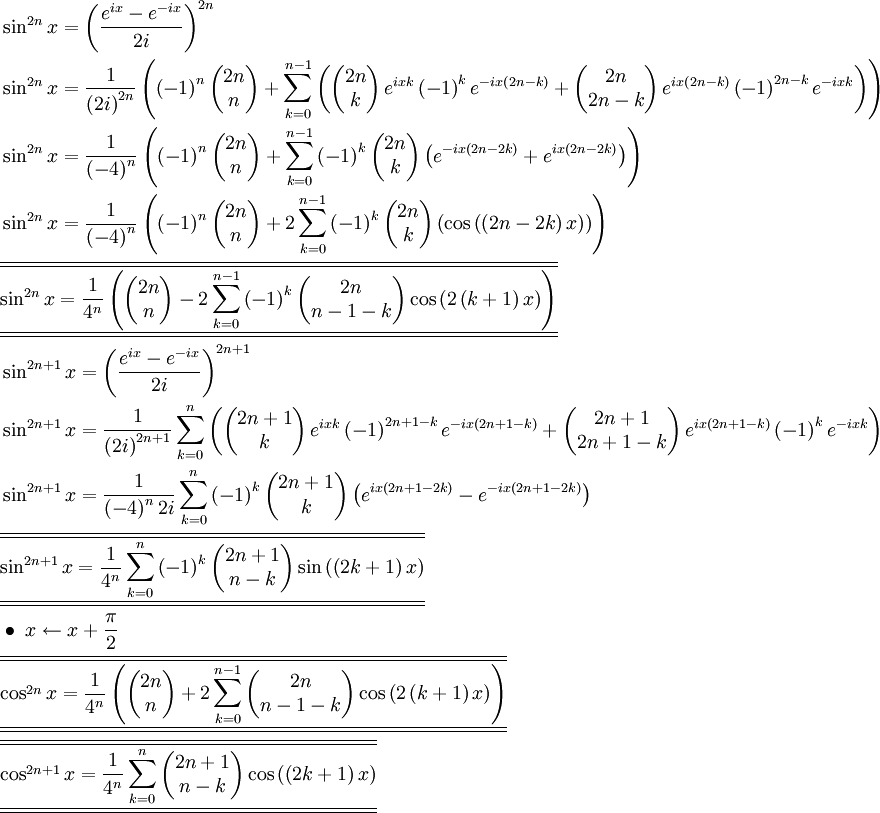
Fonctions trigonométriques réciproques
Ce sont les fonctions réciproques des fonctions sinus, cosinus et tangente.
Si x > 0 alors
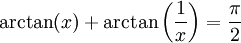 .
.
Si x < 0 alors le côté droit de l'égalité doit être remplacé par
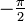 .
.Beaucoup d'identités similaires aux suivantes peuvent être obtenues à partir du théorème de Pythagore :
Propriétés métriques dans un triangle quelconque
Formule des sinus
Il suffit de voir que ha = 2S avec h = csinB donc abcsinB = 2Sb. D'autre part soit I le point de concours des bissectrices r le cercle inscrit ra + rb + rc = 2S = 2rp.
R est le rayon du cercle circonscrit.
Formule des différences des côtés
(Se rappeler que
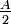 étant aigu,
étant aigu, 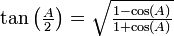 et appliquer le théorème d'Al-Kashi.
et appliquer le théorème d'Al-Kashi.Identités sans variable
Richard Feynman qui était réputé pour avoir très bien appris ses formules de trigonométrie, s'est toujours rappelé cette curieuse identité :
Une telle identité est un exemple d'identité qui ne contient pas de variable et s'obtient à partir de l'égalité :
Les relations suivantes peuvent aussi être considérées comme des identités sans variable :
Il se trouve que la mesure en degrés des angles ne donne pas une formule plus simple qu'avec la mesure en radians lorsque nous considérons cette identité avec 21 aux dénominateurs :
Mais les facteurs 1, 2, 4, 5, 8, 10 peuvent nous faire penser aux entiers inférieurs à 21/2 qui n'ont pas de facteur commun avec 21. Les derniers exemples sont des conséquences d'un résultat de base sur les polynômes cyclotomiques ; les cosinus sont les parties réelles des racines de ces polynômes ; la somme des zéros donne la valeur de la fonction de Möbius en 21 (dans le tout dernier cas qui précède) ; seulement la moitié des racines sont présentes dans la relation précédente.
En analyse
En analyse, il est essentiel que les angles qui apparaissent comme arguments de fonctions trigonométriques soient mesurés en radians ; s'ils sont mesurés en degrés ou dans n'importe quelle autre unité, alors les relations reportées ci-dessous deviennent fausses. Si les fonctions trigonométriques sont définies géométriquement, alors leurs dérivées peuvent être obtenues en établissant préalablement ces limites :
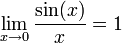 ,
,
et
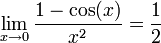 ;
;
et en utilisant alors la définition avec les limites de la dérivée en un point ainsi que les théorèmes d'addition ; si les fonctions trigonométriques sont définies par leurs séries de Taylor, alors les dérivées peuvent être obtenues en dérivant les séries entières terme à terme.
Les autres fonctions trigonométriques peuvent être dérivées en utilisant les identités précédentes et les règles de dérivation, par exemple :
Les identités sur les intégrales peuvent être trouvées dans la table d'intégrales.
Voir aussi
- Portail des mathématiques
Catégories : Analyse réelle | Identité mathématique | Trigonométrie
Wikimedia Foundation. 2010.

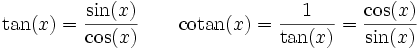
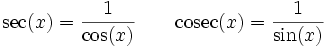
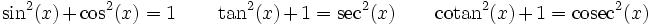
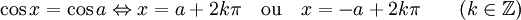
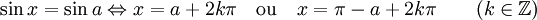
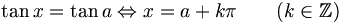
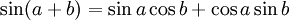
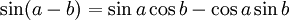
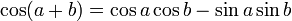
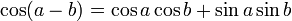
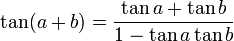
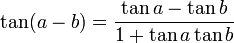
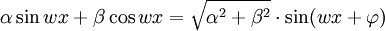
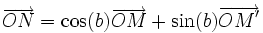
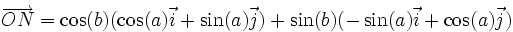
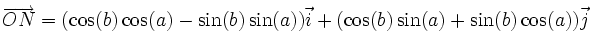
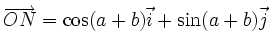
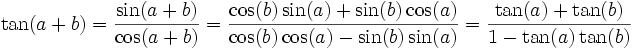
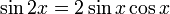
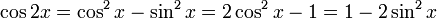
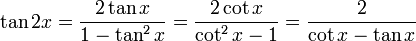
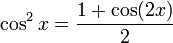
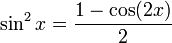
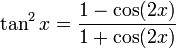
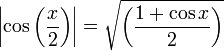
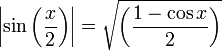
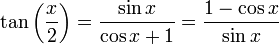
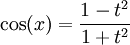
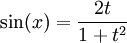
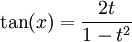
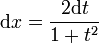
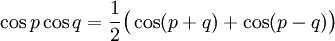
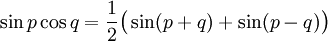
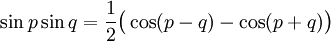
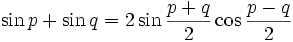
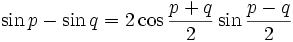
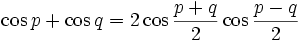
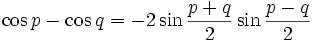
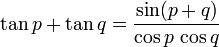
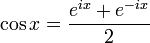
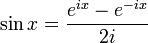
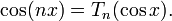
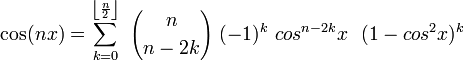
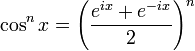
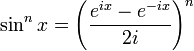
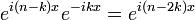
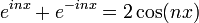
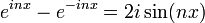
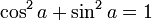
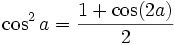
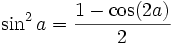
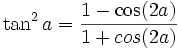
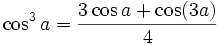
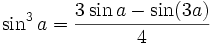
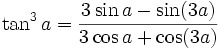
![y=\arcsin x\Leftrightarrow x=\sin y\quad \text{avec}\quad y\in\left[\frac{-\pi}{2}\, ;\frac{\pi}{2}\right]](/pictures/frwiki/54/60528daef493dab8ee2020b27776d6b1.png)
![y=\arccos x\Leftrightarrow x=\cos y\quad \text{avec}\quad y\in\left[0\, ;\pi\right]](/pictures/frwiki/98/bd3698a032d00c0454fcb2de513329f8.png)
![y=\arctan x\Leftrightarrow x=\tan y\quad \text{avec}\quad y\in\left]\frac{-\pi}{2}\, ;\frac{\pi}{2}\right[](/pictures/frwiki/101/eeee4efd2fad1b54a968b9b92de3ab9e.png)