- Méthode de simpson
-
Méthode de Simpson
 Pour les articles homonymes, voir Simpson.
Pour les articles homonymes, voir Simpson.En analyse numérique, la méthode de Simpson, du nom de Thomas Simpson est une technique de calcul numérique d'une intégrale, c'est-à-dire, le calcul approché de :
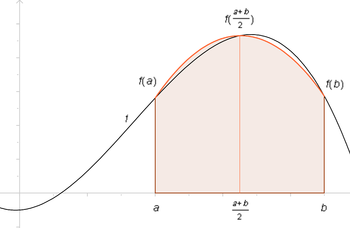
Cette méthode utilise l'approximation d'ordre 2 de f par un polynôme quadratique P prenant les mêmes valeurs que f aux points d'abscisse a, b et
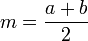 . Pour déterminer l'expression de cette parabole (polynôme de degré 2), on utilise l'interpolation lagrangienne. Le résultat peut être mis sous la forme :
. Pour déterminer l'expression de cette parabole (polynôme de degré 2), on utilise l'interpolation lagrangienne. Le résultat peut être mis sous la forme :Un polynôme étant une fonction très facile à intégrer, on approche l'intégrale de la fonction f sur l'intervalle [a,b], par l'intégrale de P sur ce même intervalle. On a ainsi, la simple formule:
Un autre moyen d'arriver à ce résultat est d'appliquer les formules de Newton-Cotes avec n=2.
Si f est 4 fois continument différentiable sur [a,b], l'erreur d'approximation vaut :
![-\frac{h^5}{90}f^{(4)}(\xi), \xi \in [a,b]](/pictures/frwiki/98/bdbb5d6a07263b5dd661b62e0d8e3edf.png) où
où 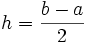
Cette expression du terme d'erreur signifie que la méthode de Simpson est exacte (c'est-à-dire que le terme d'erreur s'annule) pour tout polynôme de degré inférieur ou égal à 3. De plus, cette méthode est d'ordre 4 pour toute fonction 4 fois continument dérivable sur [a,b].
Par ailleurs, il apparait que plus l'intervalle est petit, plus l'approximation de la valeur de l'intégrale est bonne. Par conséquent, pour obtenir un résultat correct, on subdivise chaque intervalle [a,m] et [m,b] en sous intervalles et on additionne la valeur obtenue sur chaque intervalle. Soit :
où :
- n est le nombre de sous intervalles de [a,b] avec n pair,
- h = (b − a) / n est la longueur de ces sous intervalles
- xi = a + ih pour
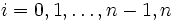 ,
, - x0 = a et xn = b.
Pour cette formule composite, le terme d'erreur devient égal à
ce qui signifie que la méthode composite fournit aussi des résultats exacts pour des polynômes de degré inférieur ou égal à trois.
À la fois cause de sa simplicité de mise en œuvre, et de sa bonne précision, cette méthode est la plus utilisée par les calculatrices pour tous calculs approchés d'intégrales de fonctions explicites.
Voir aussi
- Calcul intégral (mathématiques élémentaires)
- Formules de Newton-Cotessur Math-Linux.com
Catégorie : Intégration numérique
Wikimedia Foundation. 2010.

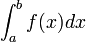
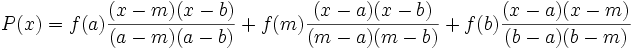
![\int_{a}^{b} f(x) dx \approx \int_{a}^{b} P(x) dx = \frac{b-a}{6}\left[f(a) + 4f\left(\frac{a+b}{2}\right)+f(b)\right]](/pictures/frwiki/99/caf08136e269c922875a7c12f3567eff.png)
![\int_a^b f(x) dx\approx
\frac{h}{3}\bigg[f(x_0)+2\sum_{j=1}^{n/2-1}f(x_{2j})+
4\sum_{j=1}^{n/2}f(x_{2j-1})+f(x_n)
\bigg],](/pictures/frwiki/52/4024d50a16ecfb7727688a2c78a78c73.png)
![n \times \frac{h^5}{180}f^{(4)}(\xi'), \xi' \in [a,b]](/pictures/frwiki/100/d3b83363b087834510bfe71b0538f69f.png)