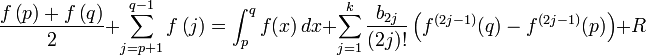Formule d'euler-maclaurin

Formule d'Euler-Maclaurin

En mathématiques, la formule d'Euler-Maclaurin est une relation entre sommes discrètes et intégrales. Elle fut découverte indépendamment, aux alentours de 1735, par le mathématicien suisse Leonhard Euler et l'écossais Colin Maclaurin. Elle peut être utilisée pour approcher des intégrales par un procédé discret, par exemple dans la méthode des trapèzes ou celle de Romberg, ou à l'inverse pour transformer une somme discrète (finie ou non) et lui appliquer les techniques du calcul infinitésimal.

Énoncé

Soient deux entiers relatifs p et q. Pour une fonction 2k fois continûment dérivable sur le segment $[p, q]$ , la formule s'énonce ainsi :

$\frac{f\left( p\right) +f\left( q\right) }{2}+\sum_{j=p+1}^{q-1}f\left( j\right) =\int_p^q f(x)\,dx +\sum_{j=1}^k\frac{b_{2j}}{(2j)!}\left(f^{(2j-1)}(q)-f^{(2j-1)}(p)\right)+R$

avec :

$R = - \int_p^q f^{(2k)}(x) {B_{2k}(x-\lfloor x \rfloor) \over (2k)!}\,dx,$

La notation $B i$ désigne le i-ème polynôme de Bernoulli, et $B_i(x-\lfloor x \rfloor)$ en est une version périodisée. Les nombres b_i désignent les nombres de Bernoulli : b₁ = −1/2, b₂ = 1/6, b₃ = 0, b₄ = −1/30, b₅ = 0, b₆ = 1/42, b₇ = 0, b₈ = −1/30.

Bien sûr, un simple changement de variable permet d'obtenir une formule analogue pour une fonction définie sur un segment à bornes non entières.

Démonstration

On se contentera de faire la démonstration sur l'intervalle $[n, n + 1]$ avec 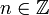$n \in \mathbb{Z}$ ; la formule précédente s'en déduit par sommation.

Soit g une fonction continûment dérivable sur $[n, n + 1]$ . En utilisant la propriété des polynômes de Bernoulli : 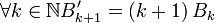$\forall k \in \mathbb{N} B_{k+1}' = \left(k+1\right) B_{k}$ , on trouve en faisant une intégration par parties :

$\int_n^{n+1} g \left( t \right) B_k \left( t-n \right) dt = \left[ \frac{g \left( t \right) B_{k+1} \left( t-n \right)}{k+1} \right]_n^{n+1} - \frac{1}{k+1} \int_n^{n+1} g' \left( t \right) B_{k+1} \left( t-n \right) dt$

Or, sachant que pour 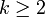$k \ge 2$ , on a $B_k \left( 1 \right) = B_k \left( 0 \right) = b_k$ , on en déduit :

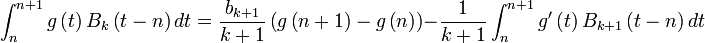
$\int_n^{n+1} g \left( t \right) B_k \left( t-n \right) dt = \frac{b_{k+1}}{k+1} \left( g \left( n+1 \right) - g \left( n \right) \right) - \frac{1}{k+1} \int_n^{n+1} g'\left( t\right) B_{k+1} \left( t-n \right) dt$

Par récurrence sur k de 0 à 2p, en prenant $g = f (2 p)$ , on obtient :

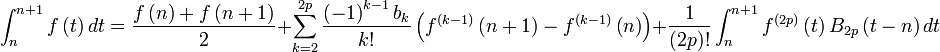
$\int_n^{n+1} f \left( t \right) dt = \frac{f\left( n\right) +f\left( n+1\right) }{2}+\sum_{k=2}^{2p} \frac{\left( -1 \right)^{k-1} b_k}{k!} \left( f^{(k-1)}\left(n+1\right) - f^{(k-1)}\left(n\right) \right) + \frac{1}{(2p)!} \int_n^{n+1} f^{(2p)} \left( t\right) B_{2p} \left( t-n \right) dt$

Enfin, avec la propriété : $\forall k \ge 1 , b_{2k+1} = 0$ , on en déduit :

$\int_n^{n+1} f \left( t \right) dt = \frac{f\left( n\right) +f\left( n+1\right) }{2}+\sum_{k=2}^{\lfloor \frac{p}{2} \rfloor} \frac{b_{2k}}{(2k)!} \left( f^{(2k-1)}\left(n+1\right) - f^{(2k-1)}\left(n\right) \right) + \frac{1}{(2p)!} \int_n^{n+1} f^{(2p)} \left( t\right) B_{2p} \left( t-n \right) dt$

Références

Analyse numérique et équations différentielles, J.-P. Demailly, Presses universitaires de Grenoble

Portail des mathématiques

Ce document provient de « Formule d%27Euler-Maclaurin ».

Catégorie : Analyse réelle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule d'euler-maclaurin de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Formule D'Euler-Maclaurin — En mathématiques, la formule d Euler Maclaurin est une relation entre sommes discrètes et intégrales. Elle fut découverte indépendamment, aux alentours de 1735, par le mathématicien suisse Leonhard Euler et l écossais Colin Maclaurin. Elle peut… … Wikipédia en Français
Formule d'Euler-Maclaurin — En mathématiques, la formule d Euler Maclaurin (appelée parfois formule sommatoire d Euler) est une relation entre sommes discrètes et intégrales. Elle fut découverte indépendamment, aux alentours de 1735, par le mathématicien suisse Leonhard… … Wikipédia en Français
Formule De Stirling — Pour les articles homonymes, voir Stirling. La formule de Stirling, du nom du mathématicien James Stirling, donne un équivalent de la factorielle au voisinage de l infini réel (quand n tend vers l infini) : que l on trouve souvent … Wikipédia en Français
Formule de stirling — Pour les articles homonymes, voir Stirling. La formule de Stirling, du nom du mathématicien James Stirling, donne un équivalent de la factorielle au voisinage de l infini réel (quand n tend vers l infini) : que l on trouve souvent … Wikipédia en Français
Euler — Leonhard Euler « Euler » redirige ici. Pour les autres significations, voir Euler (homonymie). Leonhard Euler … Wikipédia en Français
Formule de Stirling — Pour les articles homonymes, voir Stirling. La formule de Stirling, du nom du mathématicien écossais James Stirling, donne un équivalent de la factorielle au voisinage de l infini réel (quand n tend vers l infini) : que l on trouve souvent… … Wikipédia en Français
EULER (L.) — Avec Joseph Louis Lagrange, son émule plus jeune, Leonhard Euler est l’un des deux géants mathématiques qui ont dominé la science du XVIIIe siècle. Ses travaux, d’une abondance inégalée, couvrent tout le champ des mathématiques, de la mécanique… … Encyclopédie Universelle
Leonard Euler — Leonhard Euler « Euler » redirige ici. Pour les autres significations, voir Euler (homonymie). Leonhard Euler … Wikipédia en Français
Leonhard Euler — « Euler » redirige ici. Pour les autres significations, voir Euler (homonymie). Leonhard Euler Portrait par Johann Georg Brucker Naissance … Wikipédia en Français
Leonhard Paul Euler — Leonhard Euler « Euler » redirige ici. Pour les autres significations, voir Euler (homonymie). Leonhard Euler … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Formule d'euler-maclaurin