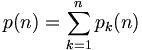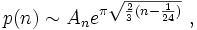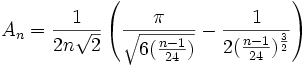Fonction partage d'un entier

En théorie des nombres, la fonction partage d'un entier, notée p(n), est une fonction qui, pour n entier, donne le nombre de toutes les façons possibles de partager l'entier naturel n, en entiers supérieurs ou égaux à 1, autrement dit le nombre de façons distinctes (ne dépendant pas de l'ordre des termes) de représenter n comme une somme d'entiers naturels. Elle n'est pas une fonction multiplicative.

Signalons que certains l'appellent « fonction de partition d'un entier » : il s'agit d'un anglicisme.

Calculs

La valeur de la fonction est facile à calculer. Une façon de faire est de définir une fonction intermédiaire, notons-la p_k, qui à un entier n fait correspondre le nombre de façons d'écrire cet entier sous forme de sommes d'exactement k termes; c'est aussi le nombre de partages de n en sommes ayant un plus grand terme égal à k.

Nous pouvons représenter un partage d'un entier n en exactement k entiers, par une k-liste décroissante 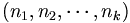$\left(n_1, n_2, \cdots, n_k\right)$ . Nous comptons les partages avec la fonction p_k en partitionnant l'ensemble des partages de l'entier n en k entiers, en deux sous-ensembles :

1. l'un formé des partages de n en exactement k entiers, tels que le kème entier soit égal à 1,

2.l'autre formé des partages en exactement k entiers dont le dernier est strictement supérieur à 1.

Il y a autant de partages dans le premier ensemble que de (k-1)-listes 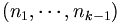$\left(n_1, \cdots, n_{k-1}\right)$ telles que 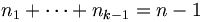$n_1+\cdots+n_{k-1}=n-1$ , c'est-à-dire autant que de partages de l'entier n-1 en exactement k-1 entiers, soit p_k-1(n-1),

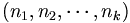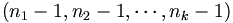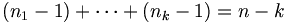Il y a autant de partages dans le second ensemble que de k-uplets décroissants $\left(n_1, n_2, \cdots, n_k\right)$ tels que $n_1+\cdots+n_{k}=n$ , soit puisque tous les entiers sont strictement supérieurs à 1, autant que k-uplets de la forme $\left(n_1-1, n_2-1, \cdots, n_k-1\right)$ tels que $(n_1-1)+\cdots+(n_{k}-1)=n-k$ et donc autant que de partages de l'entier n-k en k entiers soit p_k(n-k). Puisque les deux ensembles sont disjoints, le nombre de partages de l'entier n en somme de k entiers est égal à p_k-1(n-1)+p_k(n-k). D'où la relation :

p_k(n)=p_k-1(n-1)+p_k(n-k)

Ce que nous pouvons écrire :

p(k,n)=p(k-1,n-1)+p(k,n-k)

Les conditions initiales de cette fonction p récursive sont les suivantes :

p(k,n) = 0 si k > n

p(k,n) = 1 si k = n

Donnons les exemples de calcul pour n de 1 à 8 :

n	k	p_k(n)	écritures	n	k	p_k(n)	écritures
1	1	1	1="1"	6	1	1	6="6"
				6	2	3	6="5"+1="4"+2="3"+3
2	1	1	2="2"	6	3	3	6="4"+1+1="3"+2+1="2"+2+2
2	2	1	2="1"+1	6	4	2	6="3"+1+1+1="2"+2+1+1
				6	5	1	6="2"+1+1+1+1
3	1	1	3="3"	6	6	1	6="1"+1+1+1+1+1
3	2	1	3="2"+1
3	3	1	3="1"+1+1	7	1	1	7="7"
				7	2	3	7="6"+1="5"+2="4"+3
4	1	1	4="4"	7	3	4	7="5"+1+1="4"+2+1="3"+3+1="3"+2+2
4	2	2	4="3"+1="2"+2	7	4	3	7="4"+1+1+1="3"+2+1+1="2"+2+2+1
4	3	1	4="2"+1+1	7	5	2	7="3"+1+1+1+1="2"+2+1+1+1
4	4	1	4="1"+1+1+1	7	6	1	7="2"+1+1+1+1+1
				7	7	1	7="1"+1+1+1+1+1+1
5	1	1	5="5"
5	2	2	5="4"+1="3"+2	8	1	1	8="8"
5	3	2	5="3"+1+1="2"+2+1	8	2	4	8="7"+1="6"+2="5"+3="4"+4
5	4	1	5="2"+1+1+1	8	3	5	8="6"+1+1="5"+2+1="4"+3+1="4"+2+2="3"+3+2
5	5	1	5="1"+1+1+1+1	8	4	5	8="5"+1+1+1="4"+2+1+1="3"+3+1+1="3"+2+2+1="2"+2+2+2
				8	5	3	8="4"+1+1+1+1="3"+2+1+1+1="2"+2+2+1+1
				8	6	2	8="3"+1+1+1+1+1="2"+2+1+1+1+1
				8	7	1	8="2"+1+1+1+1+1+1
				8	8	1	8="1"+1+1+1+1+1+1+1

etc.

Pour obtenir p(n), il suffit ensuite de calculer la somme :

$p(n)=\sum_{k=1}^n p_{k}(n)$

Dans notre exemple, les valeurs de p(1) à p(8) sont donc :

p(1) = 1
p(2) = 1 + 1 = 2
p(3) = 1 + 1 + 1 = 3
p(4) = 1 + 2 + 1 + 1 = 5
p(5) = 1 + 2 + 2 + 1 + 1 = 7
p(6) = 1 + 3 + 3 + 2 + 1 + 1 = 11
p(7) = 1 + 3 + 4 + 3 + 2 + 1 + 1 = 15
p(8) = 1 + 4 + 5 + 5 + 3 + 2 + 1 + 1 = 22

Les valeurs suivantes de p(n) sont :

p(9) = 30
p(10) = 42
p(50) = 204226
p(100) = 190569292
p(200) = 3972999029388
p(1000) = 24061467864032622473692149727991

Il a été démontré que si n se termine par 4 ou 9, alors p(n) est divisible par 5.

Méthode plus rapide

Il existe une autre méthode de calcul du nombre de partitions d'un entier qui se base sur le Théorème du nombre pentagonal d'Euler. Celui-ci donne une relation amusante qui lie p(n) aux p(i) pour $i < = n$ .

Cette relation est :

$p (n) = p (n - 1) + p (n - 2) - p (n - 5) - p (n - 7) + p (n - 12) + p (n - 15)...$ où les termes de cette somme sont

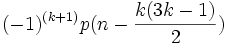$(-1)^{(k+1)} p(n-{k(3k-1) \over 2 })$ lorsque cette expression a un sens, avec $k$ entier relatif. Les nombres 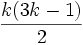$k(3k-1)\over 2$ sont les nombres pentagonaux généralisés.

Estimation asymptotique

Hardy et Ramanujan ont présenté en 1918 une fonction approximative de p(n) ; à savoir :

$p(n) \sim A_n e^{\pi \sqrt{\frac{2}{3}(n-\frac{1}{24})}}\ ,$

quand

$A_n = \frac{1}{2n\sqrt{2}}\left(\frac{\pi}{\sqrt{6(\frac{n-1}{24})}}-\frac{1}{2(\frac{n-1}{24})^\frac{3}{2}}\right)$

La correction très énigmatique 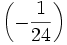$\left(-\frac{1}{24}\right)$ , inventée par Ramanujan, fait que p(200) est exact !

Plus tard, ils obtinrent une égalité stricte pour calculer p(n).

Série de Rademacher

En affinant la méthode employée par Hardy et Ramanujan, Rademacher démontra en 1937 la formule suivante:

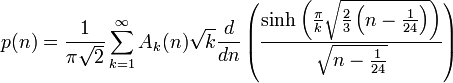
$p(n) = \frac{1}{\pi \sqrt{2}} \sum_{k=1}^{\infty}{A_k(n)\sqrt{k} \frac{d}{dn}\left( \frac{\sinh \left( \frac{\pi}{k} \sqrt{\frac{2}{3} \left( n-\frac{1}{24}\right)}\right)}{\sqrt{n-\frac{1}{24}}}\right)}$

avec 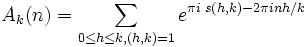$A_k(n) = \sum_{0 \leq h \leq k, (h,k)=1}{e^{\pi i\; s(h,k) - 2 \pi i n h/k}}$ et $s (h, k)$ la somme de Dedekind. Le démonstration de cette formule fait intervenir les suites de Farey, les cercles de Ford, et l'analyse complexe.

Références

Tom Apostol, Modular Functions and Dirichlet Series in Number Theory, Springer

Portail des mathématiques

Ce document provient de « Fonction partage d%27un entier ».

Catégorie : Fonction arithmétique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction partage d'un entier de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Fonction Partage D'un Entier — En théorie des nombres, la fonction partage d un entier, notée p(n), est une fonction qui, pour n entier, donne le nombre de toutes les façons possibles de partager l entier naturel n, en entiers supérieurs ou égaux à 1, autrement dit le nombre… … Wikipédia en Français
Partage d'un entier — Partition d un entier Une partition d un entier strictement positif n est une façon d écrire n comme une somme d entiers strictement positifs. Deux sommes qui diffèrent seulement de l ordre de leurs opérandes sont considérées comme étant la même… … Wikipédia en Français
Partage (concept) — Partage Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le partage est l action de transformation d un élément en plusieurs autres. Pour ce faire, l unité première peut : soit être divisée en… … Wikipédia en Français
Partage en commun — Partage Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le partage est l action de transformation d un élément en plusieurs autres. Pour ce faire, l unité première peut : soit être divisée en… … Wikipédia en Français
Fonction Arithmétique — En théorie des nombres, une fonction arithmétique f est une fonction définie sur l ensemble des entiers naturels non nuls, et à valeurs dans l ensemble des nombres complexes. En d autres termes, une fonction arithmétique n est rien d autre qu une … Wikipédia en Français
Fonction arithmetique — Fonction arithmétique En théorie des nombres, une fonction arithmétique f est une fonction définie sur l ensemble des entiers naturels non nuls, et à valeurs dans l ensemble des nombres complexes. En d autres termes, une fonction arithmétique n… … Wikipédia en Français
Partage — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le partage est l action de transformation d un élément en plusieurs autres, à des fins de mise à disposition à plusieurs personnes ou entités. Pour ce… … Wikipédia en Français
Fonction arithmétique — En théorie des nombres, une fonction arithmétique f est une fonction définie sur l ensemble des entiers naturels non nuls, et à valeurs dans l ensemble des nombres complexes. En d autres termes, une fonction arithmétique n est rien d autre qu une … Wikipédia en Français
entier — entier, ière [ ɑ̃tje, jɛr ] adj. et n. m. • XIe; lat. integer « non touché », de tangere « toucher »; cf. intégral 1 ♦ Dans toute son étendue. ⇒ total. Manger un pain entier. ⇒ tout (tout un, tout le). Payer place entière, sans réduction,… … Encyclopédie Universelle
Fonction étagée — En mathématiques et en analyse : Une fonction simple est une fonction numérique dont l image est constituée d’un nombre fini de valeurs réelles (ou éventuellement complexes). Une fonction étagée est une fonction simple définie sur un espace… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction partage d'un entier