- Fonction numerique
-
Fonction numérique

Cet article fait partie de la série
Mathématiques élémentairesAlgèbre Logique Arithmétique Probabilités Statistiques Lorsque nous exprimons qu’une quantité dépend d’une autre quantité nous supposons qu’il existe un moyen d’obtenir cette quantité à partir d’une autre. Et si ces quantités sont représentées par des variables, alors une variable est fonction d’une autre, quand il y a une règle qui permet d’obtenir la valeur de cette variable, à partir de la valeur de l’autre.
Exemple: la quantité "chiffre d'affaire" d'une entreprise dépend de la quantité "nb de produits vendus"
Une fonction numérique est une règle qui permet d'associer à un réel un autre nombre réel.
Donnons l’exemple d’un épicier qui augmente les prix de tous ses articles de 20%. Ajouter à chaque prix 20% du prix, revient à multiplier chaque prix par 120%. La règle que l’épicier va appliquer à chaque prix est la multiplication par 1,2 et nous dirons que le nouveau prix est fonction de l’ancien.Sommaire
Définition
Une fonction numérique f ou fonction réelle d’une variable réelle d’une partie D de
 dans
dans  , est une correspondance (ou application) qui à tout élément x de D associe un réel et un seul noté f(x).
, est une correspondance (ou application) qui à tout élément x de D associe un réel et un seul noté f(x).
Ce réel f(x) est l’image de x par f.Cette partie D de
 est appelée l’ensemble de définition de f.
est appelée l’ensemble de définition de f.Notation
Nous notons la fonction :
(observez que la seconde flèche possède un poussoir que n'a pas la première)
- ou plus simplement
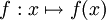
Exemple
Soit la fonction qui à tout nombre réel de l'intervalle [ − 1; + 1] associe son carré diminué de 1.
Nous pouvons définir la fonction f des manières suivantes :
Soit f définie par :
- pour tout réel x dans
![[ -1 ; +1 ],\ f(x) = x^2 - 1 ~](/pictures/frwiki/51/3ea461ea68e0eddbd4a076c064e58f3d.png)
ou encore :
Remarque
Nous ne devons pas confondre f et f(x). Dans l’exemple précédent f est la règle qui élève un réel au carré et lui retranche 1, tandis que f(x) est égal au réel x²-1 qui est associé à x.
Ensemble de définition
Soit f une fonction de D dans
 .
.
Soit x un réel. Si x appartient à D, alors on dit que f est définie en x, et si x n’appartient pas à D on dit que f n’est pas définie en x.Remarques
- L'ensemble de définition d'une fonction peut être donné dans l'énoncé définissant la fonction et sinon il doit être déterminé.
- Rechercher l’ensemble de définition ou le domaine de définition d’une fonction, c’est déterminer les réels x tels que f(x) existe.
Erreurs classiques
Bon nombre de lycéens tiennent pour vraie la relation f(a+b)=f(a)+f(b) :
- pour la fonction carré, cela donnerait (a+b)²=a²+b², ce qui est faux (voir identité remarquable) ;
- pour la fonction sinus, cela donnerait sin(a+b)=sin(a)+sin(b) donc 0=sin(180°)=sin(90°+90°)=sin(90°)+sin(90°)=2, soit 0=2 (voir fonction trigonométrique)
- pour la fonction logarithme, cela donnerait ln(a+b)=ln(a)+ln(b) donc ln(2)=ln(1)+ln(1)=0, ce qui est encore faux.
En fait la confusion vient de l’application abusive des règles de calcul uniquement valables pour les fonctions linéaires, en d’autres mots pour les situations de proportionnalité.
Voir aussi
Catégories : Mathématiques élémentaires | Analyse
Wikimedia Foundation. 2010.

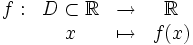
![\begin{matrix}f: & [-1;1] & \rightarrow & \mathbb R\\ & x & \mapsto & f(x) = x^2-1\end{matrix}](/pictures/frwiki/50/2ec32b6dccbfd466c6ea341ebdf5de66.png)