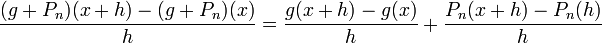- Fonction continue dérivable nulle part
-
Fonction continue nulle part dérivable
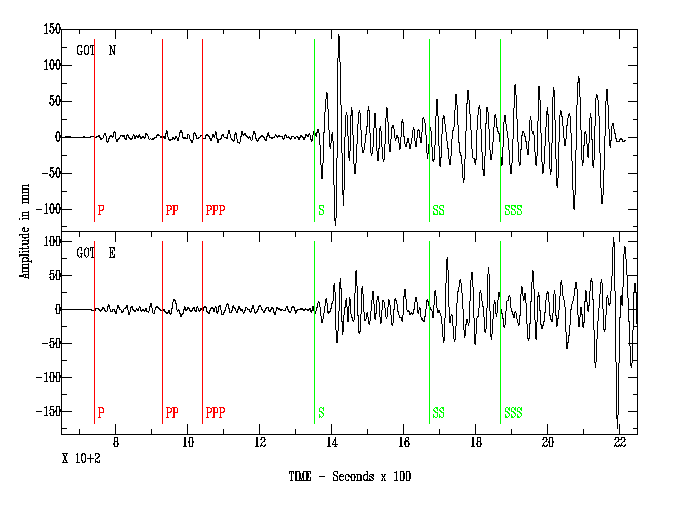 Sismogramme du Tremblement de terre de 1906 à San Francisco, bien que continue, cette courbe n'est pas « arrondie ».
Sismogramme du Tremblement de terre de 1906 à San Francisco, bien que continue, cette courbe n'est pas « arrondie ».
En mathématiques, une fonction continue nulle part dérivable est une fonction numérique qui est régulière du point de vue topologique (c'est-à-dire continue) mais ne l'est pas du tout du point de vue du calcul différentiel (c'est-à-dire qu'elle n'est dérivable en aucun point).
La continuité d'une fonction signifie que sa courbe représentative n'admet pas de « cassure ». La dérivabilité assure qu'elle est bien « arrondie ». Il est assez aisé de démontrer que tout fonction dérivable sur un intervalle est continue sur ce même intervalle. Les mathématiciens ont cru, jusqu'au XIXe siècle que la réciproque était en partie vraie, que les points où une fonction continue n'est pas dérivable sont rares. Il n'en est rien. De nombreux contre-exemples furent découverts. Il fut même démontré que ces fonctions sont les plus communes.
Depuis, l'étude de ces fonctions a montré qu'elles étaient importantes, non seulement du point de vue de la logique interne aux mathématiques, pour comprendre le concept de fonction, mais également pour fournir des modèles utiles aux autres sciences. Ainsi, en cinématique, la courbe d'une fonction dont la variable est le temps représente la trajectoire d'un mobile. La dérivée est la vitesse instantanée. Un fonction continue nulle part dérivable modélise la trajectoire d'un mobile qui change de direction à chaque instant, ce qui correspond au mouvement brownien d'une particule mais aussi aux cours de bourse étudiés par les mathématiques financières. Les fractales donnent également des exemples de courbes continues sans tangentes.
Sommaire
Histoire
Le concept même de fonction ne s'est clarifié qu'au XIXe siècle, lorsqu'en 1837, Dirichlet pose une définition moderne du concept de fonction.
Définition — Une quantité y est une fonction (univoque) d'une quantité x, dans un intervalle donné quand à chaque valeur attribuée à x dans cet intervalle correspond une valeur unique et déterminée de y, sans rien spécifier sur la façon dont les diverses valeurs de y s'enchaînent les unes aux autres[1].
À cette époque, la plupart des mathématiciens pensaient qu'une fonction continue était dérivable, sauf sur un ensemble discret de points[2]. Par exemple, André-Marie Ampère essaya de prouver que toute fonction est dérivable, sauf éventuellement en un nombre fini de points dans une publication de 1806[3], sans cependant clarifier ce qu'il entendait par fonction[2]. C'est pourquoi Bernhard Riemann étonna la communauté mathématique quand il exhiba, lors d'une conférence en 1861, un exemple de fonction qui est continue sur R mais dérivable seulement en de rares points[2]. Cette fonction est définie par
et n'est dérivable en x que lorsque x =
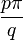 où p et q sont des entiers impairs.
où p et q sont des entiers impairs.En 1872, Karl Weierstrass fut le premier à publier non seulement une, mais tout une famille de fonctions continues et nulle part dérivables. Elles sont définies par
avec où a et b sont des constantes réelles, a étant dans ]0,1[ et le produit ab strictement supérieur à 1 + 3π⁄2. Après cette découverte, des mathématiciens en trouvèrent d'autres[2].
On alla même plus loin en prouvant que pour une fonction continue arbitraire, il existe une fonction continue partout et nulle part dérivable aussi proche d'elle que l'on désire. Cela signifie que ces fonctions particulières sont particulièrement nombreuses et forment un "gros" ensemble d'un point de vue topologique.
L'intérêt d'introduire ces fonctions, que l'on qualifie parfois de pathologiques, fut parfois rejeté par les mathématiciens. Citons par exemple Charles Hermite qui déclara en 1893 :
« Je me détourne avec effroi et horreur de cette plaie lamentable des fonctions continues qui n'ont point de dérivées.[4] »ou encore Henri Poincaré qui qualifie ces fonctions de « monstres »[Note 1].
La découverte de l'existence de ces fonctions a profondément modifié la vision qu'avaient les mathématiciens du concept de fonction et de celui de courbe. Les fonctions numériques réelles continues sont parfois présentées comme étant celles dont on peut tracer la courbe « sans lever le crayon »[5]. Or, le graphe d'une fonction continue nulle part dérivable ne peut pas être tracé.
Ces fonctions sont encore considérées, au tournant des années 2000, comme contre-intuitives et comme un facteur bloquant pour l'apprentissage des mathématiques :
« Bien entendu, on sait maintenant qu’il existe des fonctions continues nulle part dérivables, mais, au niveau de l’enseignement secondaire, il n’y a aucun inconvénient à s'appuyer sur l’intuition contraire.[6] »Mandelbrot, l'inventeur des fractales, soutient au contraire que les courbes continues sans tangentes sont intuitives, mais reconnaît qu'il n'a trouvé, parmi ses prédécesseurs, que deux mathématiciens partageant cette opinion[7].
Un exemple
L'article fonction de Weierstrass présente un exemple historique d'une classe de fonctions continues partout nulle part dérivables. Nous allons en donner une autre.
On définit une fonction par
On peut la prolonger par périodicité sur tous les réels en posant pour tout x réel
- g(x + 4) = g(x)
On pose alors
Cette fonction est continue sur
 , mais n'est dérivable en aucun point de
, mais n'est dérivable en aucun point de  .
.Principe de la construction. La fonction f est limite uniforme de fonctions fn définies par :
Ces fonctions fn sont continues, affines par morceaux, mais leurs représentations graphiques sont formées de segments de droites dont les pentes sont de plus en plus raides.
Démonstration-
- Continuité
Par définition de g, on a
Or on sait que
∑ 2 − k k est convergente (voir série géométrique), donc la suite (fn) converge uniformément vers f. Comme, de plus
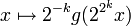 est continue sur
est continue sur  , il en est de même de fn et de sa limite uniforme f.
, il en est de même de fn et de sa limite uniforme f.-
- Dérivabilité
Soit
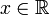 . On va construire une suite de réels (hn) convergeant vers 0 et telle que
. On va construire une suite de réels (hn) convergeant vers 0 et telle quece qui assurera que f n'est pas dérivable en x.
Pour ce x fixé et pour tout
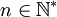 , on choisit
, on choisit 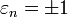 tel que
tel que 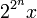 et
et 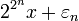 soient dans le même intervalle de la forme [2N;2N + 2]. On pose alors
soient dans le même intervalle de la forme [2N;2N + 2]. On pose alors 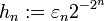 .
.- Pour k > n, on sait que
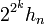 est un multiple de 4, et comme g est de période 4, on a
est un multiple de 4, et comme g est de période 4, on a
- Pour k = n, on a
- Pour k < n, comme on sait, par construction de la fonction g que
-
- (la pente de la droite joignant deux points de Cg est toujours comprise entre -1 et 1). On a en particulier
- donc
On peut donc le taux d'accroissement de f en x :
Ceci montre que f n'est pas dérivable en x, or ce point est arbitraire, donc f n'est dérivable en aucun point de
 .
.Densité
Théorème — Toute fonction continue sur [0,1] est limite uniforme de fonctions continues nulle part dérivables sur [0,1].
Cela signifie que pour une fonction
![f:[0,1] \rightarrow \R](/pictures/frwiki/48/061d8197e20e9853f16cbd308ba889c8.png) continue fixée et pour un
continue fixée et pour un 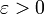 arbitraire, il existe une fonction
arbitraire, il existe une fonction ![g:[0,1] \rightarrow \R](/pictures/frwiki/101/e0b6ade2baa967bcf3df1f99dc58223b.png) continue nulle part dérivable telle que
continue nulle part dérivable telle queEn d'autres termes, cela signifie que l'ensemble des fonctions continues et nulle part dérivable est dense dans l'ensemble des fonctions continues, pour la topologie de la convergence uniforme.
On peut énoncer un résultat analogue sur
 : toute fonction continue sur
: toute fonction continue sur  est localement limite uniforme de fonctions continues nulle part dérivables.Démonstration
est localement limite uniforme de fonctions continues nulle part dérivables.DémonstrationSoit
![f:[0,1] \rightarrow \R](/pictures/frwiki/48/061d8197e20e9853f16cbd308ba889c8.png) continue. On a vu d'après la section précédente qu'il existe au moins une fonction
continue. On a vu d'après la section précédente qu'il existe au moins une fonction ![g:[0,1] \rightarrow \R](/pictures/frwiki/101/e0b6ade2baa967bcf3df1f99dc58223b.png) continue partout nulle part dérivable. On sait alors que f − g est une fonction continue de [0,1] dans
continue partout nulle part dérivable. On sait alors que f − g est une fonction continue de [0,1] dans  , donc d'après le théorème de Stone-Weierstrass, il existe une suite
, donc d'après le théorème de Stone-Weierstrass, il existe une suite 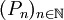 de fonctions polynômiales de [0,1] dans
de fonctions polynômiales de [0,1] dans  telle que
telle queOn a donc
La fonction f est donc limite uniforme sur [0,1] de la fonction g + Pn, qui est continue comme somme de fonctions continues mais nulle part dérivable sur [0,1]. En effet, soit
![x \in [0,1]](/pictures/frwiki/99/c628ba2b1047de93f66cb815d986e107.png) . On a
. On aOr le premier terme de la somme diverge quand
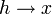 car g n'est pas dérivable en x, mais le second terme converge vers P'n(x), qui existe car une fonction polynômiale est infiniment dérivable.
car g n'est pas dérivable en x, mais le second terme converge vers P'n(x), qui existe car une fonction polynômiale est infiniment dérivable.On peut également fournir une démonstration non constructive (c'est-à-dire ne nécessitant pas d'exhiber un exemple de fonction continue nulle part dérivable) utilisant le lemme de Baire[8].
Annexes
Bibliographie
- Benoît Mandelbrot, Les objets fractals, 4e édition, Flammarion, 1995 (ISBN 2080813013).
L'ouvrage de référence sur les fractales, leur découverte, leurs applications, par leur inventeur.
- Henri Poincaré, Science et méthode, Flammarion, 1908
- (en) Johan Thim, Continuous Nowhere Differentiable Functions, 2003.
Une thèse. Étude complète de l'histoire des fonctions continues nulle part dérivables.
Notes
- ↑ La citation exacte est :
Poincaré 1908, p. 132.« La logique parfois engendre des monstres. On vit surgir toute une foule de fonctions bizarres qui semblaient s'efforcer de ressembler aussi peu que possible aux honnêtes fonctions qui servent à quelque chose. Plus de continuité, ou bien de la continuité, mais pas de dérivées[...] Autrefois, quand on inventait une fonction nouvelle, c'était en vue de quelque but pratique ; aujourd'hui, on les invente tout exprès pour mettre en défaut les raisonnements de nos pères, et on n'en tirera jamais que cela. »
Références
- ↑ Encyclopédie des sciences mathématiques pures et appliquées, Gauthier-Villard, 1909.
- ↑ a , b , c et d Johan Thim 2003.
- ↑ A. Ampère, Recherches sur quelques points de la théorie des fonctions dérivées qui conduisent à une nouvelle démonstration de la série de Taylor, et à l'expression finie de termes qu'on néglige lorsqu'on arrête cette série à un ordre quelconque, Journal de l'Ecole Polytechnique, No. 13, p. 148-191 (1806)
- ↑ Lettre 374 d'Hermite à Stieljtes du 20 mai 1893, Correspondance d’Hermite et de Stieltjes, éd. B. Baillaud et H. Bourget. vol 2, Gauthier-Villars, 1905, p.317-319
- ↑ Par exemple le programme officiel de mathématiques de 2001 des classes de terminale S en France.
- ↑ Rapport d'étape sur la géométrie et son enseignement, Commission de réflexion sur l’enseignement des mathématiques, Janvier 2000, dit rapport Kahane, sur le site de la Société mathématique de France.
- ↑ Mandelbrot 1995, chap. II.
- ↑ Xavier Gourdon, Les maths en tête : analyse, éditions Ellipses
Articles connexes
- Cas pathologique
- Fractales Les courbes des fonctions continues partout nulle part dérivables ont souvent des structures de fractales, et inversement les fractales fournissent des exemples de telles fonctions.
Liens externes
- Portail des mathématiques
Catégories : Analyse réelle | Fonction remarquable | Fractale
Wikimedia Foundation. 2010.

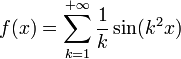
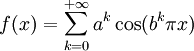
![g(x):=\begin{cases} 1+x & \text{si } x \in [-2,0] \\ 1-x & \text{si } x \in [0,2] \end{cases}](/pictures/frwiki/48/024e468083ea1fec8faa476ab5d04b3b.png)
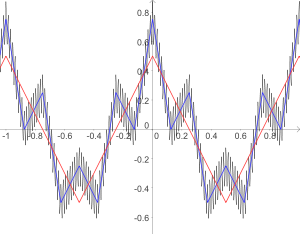
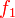 ,
,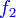 et
et dont
dont  est la limite
est la limite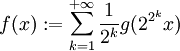
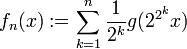
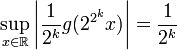
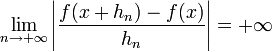
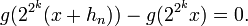
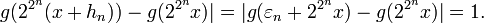
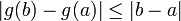
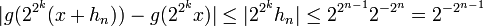
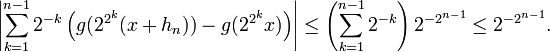
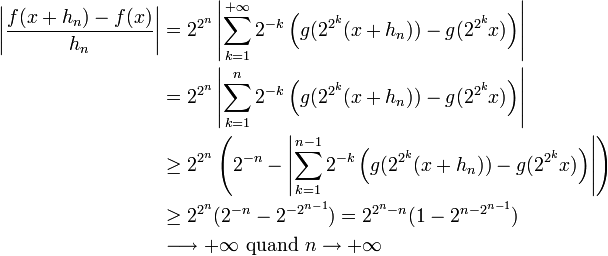
![\sup_{t \in [0,1]} |f(t) -g(t)| < \varepsilon.](/pictures/frwiki/101/e5293c96fda68293624f8bfaa27b23b0.png)
![\sup_{t \in [0,1]} |(f-g)(t) -P_n(t)| \underset{n \rightarrow +\infty}{\longrightarrow} 0](/pictures/frwiki/98/b61f8f7f4543cb95d7fb7097a93e731c.png)
![\sup_{t \in [0,1]} |f(t) -(g+P_n)(t)| \underset{n \rightarrow +\infty}{\longrightarrow} 0](/pictures/frwiki/55/752810d74c51767dc61f86139f33e5a3.png)