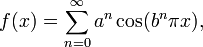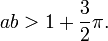Fonction de weierstrass

Fonction de Weierstrass

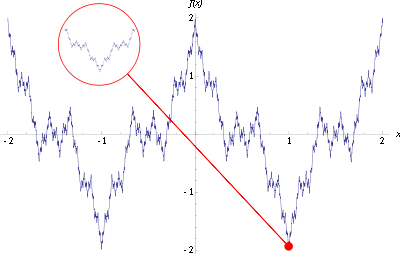
Représentation de la fonction de Weierstrass sur l'intervalle [-2,2]. La fonction a un comportement fractal : n'importe quel zoom (par exemple le cercle rouge) ressemble au zoom total.

La fonction de Weierstrass fut le premier exemple publié^[1] d'une fonction qui est continue partout mais qui n'est dérivable à aucun endroit. On la doit à Karl Weierstrass et Leopold Kronecker même s'il semble que la propriété concernant la dérivée fut découverte par Bernhard Riemann en 1861^[2].

Il s'agit en fait d'un groupe de fonctions qui peut être défini comme suit :

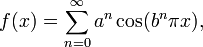
$f(x)=\sum_{n=0}^\infty a^n\cos(b^n\pi x),$

où $0 < a < 1$ et

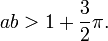
$ab>1+\frac{3}{2}\pi.$

Ce qui rend cette fonction intéressante est ses caractéristiques similaires aux fractales dans le sens où elle a une complexité uniforme et infinie, indépendamment du facteur d'échelle avec lequel on la considère.

L'hypothèse ab > 1 (G. H. Hardy) suffit, mais la preuve est sensiblement plus difficile.

Voir aussi

Fonction continue nulle part dérivable

Références

↑ K. Weierstrass. Über continuirliche Funktionen eines reellen Arguments, die für keinen Werth des letzteren einen bestimmten Differentialquotienten besitzen, 1967. in Karl Weiertrass Mathematische Werke, Abhandlungen II, Johnson, Gelesen in der Königl. Akademie der Wissenchaften am 18 Juli 1872
↑ Weierstrass Function -- from Wolfram MathWorld

Portail des mathématiques

Ce document provient de « Fonction de Weierstrass ».

Catégories : Analyse réelle | Fonction remarquable

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction de weierstrass de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Fonction De Weierstrass — Représentation de la fonction de Weierstrass sur l intervalle [ 2,2]. La fonction a un comportement fractal : n importe quel zoom (par exemple le cercle rouge) ressemble au zoom total. La fonction de Weierstrass fut le premier exemple… … Wikipédia en Français
Fonction de Weierstrass — Ne pas confondre avec les fonctions elliptiques de Weierstrass ou la fonction zêta de Weierstrass. Représentation de la fonction de Weierstrass sur l intervalle [ 2,2]. La fonction a un comporte … Wikipédia en Français
Fonction Zeta De Weierstrass — Fonction zêta de Weierstrass En mathématiques, les fonctions de Weierstrass sont des fonctions spéciales d une variable complexe qui sont reliées à la fonction elliptique de Weierstrass . Sommaire 1 Fonction sigma Weierstrass 2 Fonction zêta de… … Wikipédia en Français
Fonction zeta de Weierstrass — Fonction zêta de Weierstrass En mathématiques, les fonctions de Weierstrass sont des fonctions spéciales d une variable complexe qui sont reliées à la fonction elliptique de Weierstrass . Sommaire 1 Fonction sigma Weierstrass 2 Fonction zêta de… … Wikipédia en Français
Fonction zeta de weierstrass — Fonction zêta de Weierstrass En mathématiques, les fonctions de Weierstrass sont des fonctions spéciales d une variable complexe qui sont reliées à la fonction elliptique de Weierstrass . Sommaire 1 Fonction sigma Weierstrass 2 Fonction zêta de… … Wikipédia en Français
Fonction continue dérivable nulle part — Fonction continue nulle part dérivable Sismogramme du Tremblement de terre de 1906 à San Francisco, bien que continue, cette courbe n est pas « arrondie ». En mathématiques, une fonction continue nulle part dérivable est une fonction… … Wikipédia en Français
Fonction Elliptique — En analyse complexe, une fonction elliptique est, grossièrement parlant, une fonction définie sur le plan complexe qui est doublement périodique (périodique dans deux directions). Elle peut être vue comme analogue à une fonction trigonométrique… … Wikipédia en Français
FONCTION (NOTION DE) — FONCTION NOTION DE Le terme de fonction a été introduit par Leibniz (1692) dans un contexte géométrique: il s’agit pour lui de portions de lignes droites qui dépendent d’un point variable sur une courbe, comme la tangente ou la normale. Jean… … Encyclopédie Universelle
Weierstrass — Karl Weierstrass Karl Weierstrass Karl Theodor Wilhelm Weierstrass Naissance 31 octobre 1815 Ostenfelde (Westphalie) … Wikipédia en Français
Fonction zêta de Weierstrass — En mathématiques, les fonctions de Weierstrass sont des fonctions spéciales d une variable complexe qui sont reliées à la fonction elliptique de Weierstrass . Sommaire 1 Fonction sigma Weierstrass 2 Fonction zêta de Weierstrass … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction de weierstrass