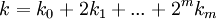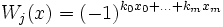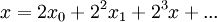Fonction de walsh

Fonction de Walsh

1  ----------------
2  --------________
3  ----________----
4  ----____----____
5  --____----____--
6  --____--__----__
7  --__--____--__--
8  --__--__--__--__

Table des huit premières fonctions orthogonales d'une base orthogonale

Les fonctions de Walsh sont un ensemble de fonctions qui forment une base orthogonale sur l'intervalle $[0;1]$ pour les fonctions qui respectent la condition suivante :

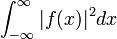$\int_{-\infty}^{\infty} {|f(x)|^2 dx}$ est finie.

Ces fonctions prennent uniquement les valeurs -1 et 1, sur des sous-intervalles définis par les fonctions dyadiques. Elles sont utiles en électronique et d'autres applications en ingénierie.

Les fonctions orthogonales de Walsh sont utilisées pour effectuer les transformées de Hadamard, qui sont très similaires aux sinusoïdales orthogonales employées dans le cadre de la transformée de Fourier. Les fonctions de Walsh partagent également des similitudes avec l'ondelette de Haar. Le système de Haar est toutefois préférable dans certaines situations où la localisation est nécessaire (alors que les fonctions de Walsh sont bornées) ou d'autres caractéristiques propres aux ondelettes doivent être respectées.

L'ordre de la fonction est 2^s, où s est un entier, ce qui implique qu'il y a 2^s intervalles où la valeur est égale à -1 ou 1.

Une liste de 2^s fonctions de Walsh forme une matrice de Hadamard. Une manière de définir les fonctions de Walsh consistent à utiliser la représentation binaire des entiers et des réels. Pour un entier k, on considère la représentation binaire suivante :

$k = k_0 + 2k_1 + ... + 2^m k_m~$

pour un entier m avec k_i égale à 0 ou 1. Ensuite, si k est le résultat en code Gray de j-1, alors la j^e fonction de Walsh au point x, avec 0 ≤ x < 1, est :

$W_j(x) = (-1)^{k_0 x_0 + ... + k_m x_m}$

$~x = 2x_0 + 2^2 x_1 + 2^3 x + ...$

où x_i est 0 ou 1.

Les fonctions de Walsh peuvent être perçues comme les caractères de :

$~(Z_2)^N$ ,

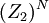le groupe de séquences sur Z₂. Vu sous cet angle, plusieurs généralisations ont été proposées.

Applications

Les applications en mathématiques peuvent être trouvées où des représentations numériques sont utilisées, par exemple dans l'analyse des méthodes numériques de quasi-Monte Carlo.

Voir aussi

Liens internes

Méthode de Monte-Carlo

Portail des mathématiques
Portail de la physique

Ce document provient de « Fonction de Walsh ».

Catégories : Algorithme numérique | Probabilités | Hasard et aléatoire | Physique statistique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction de walsh de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Fonction De Walsh — 1 2 3 4 5 6 7 8 Table des huit premières fonctions orthogonales d une base orthogonale Les fonctions de Walsh sont un ensemble de fonctions qui forment une base orthogonale sur l intervalle [0;1] pour les fonctions qui respectent la condition… … Wikipédia en Français
Fonction de Walsh — 1 2 3 4 5 6 7 8 Table des huit premières fonctions orthogonales d une base orthogonale Les fonctions de Walsh sont un ensemble de fonctions qui forment une base orthogonale sur l intervalle [0;1] pour les fonctions qui respectent la condition… … Wikipédia en Français
Walsh — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Patronyme 2 Personnage fictif 3 … Wikipédia en Français
Fonction Booléenne — Une fonction booléenne est une fonction de dans où désigne le corps fini à 2 éléments. En fait, les fonctions booléennes sont simplement un autre nom des fonctions logiques. Toutefois, lorsque l on s attache aux propriétés algébriques de ces… … Wikipédia en Français
Fonction booleenne — Fonction booléenne Une fonction booléenne est une fonction de dans où désigne le corps fini à 2 éléments. En fait, les fonctions booléennes sont simplement un autre nom des fonctions logiques. Toutefois, lorsque l on s attache aux propriétés… … Wikipédia en Français
Fonction Courbe — Une fonction booléenne avec un nombre pair de variables est dite fonction courbe bent dans la terminologie anglosaxonne si sa non linéarité est maximale. Cela correspond à être à distance maximale pour la distance de Hamming de l ensemble des… … Wikipédia en Français
Fonction bent — Fonction courbe Une fonction booléenne avec un nombre pair de variables est dite fonction courbe bent dans la terminologie anglosaxonne si sa non linéarité est maximale. Cela correspond à être à distance maximale pour la distance de Hamming de l… … Wikipédia en Français
Fonction booléenne — Une fonction booléenne est une fonction de dans où désigne le corps fini à 2 éléments. En fait, les fonctions booléennes sont simplement un autre nom des fonctions logiques. Toutefois, lorsque l on s attache aux propriétés algébriques de ces… … Wikipédia en Français
Fonction courbe — Une fonction booléenne avec un nombre pair de variables est dite fonction courbe bent dans la terminologie anglosaxonne si sa non linéarité est maximale. Cela correspond à être à distance maximale pour la distance de Hamming de l ensemble des… … Wikipédia en Français
Transformee de Walsh — Transformée de Walsh En mathématiques, et plus précisément en analyse harmonique la transformée de Walsh est l analogue de la Transformée de Fourier discrète. Elle opère sur un corps fini de l arithmétique modulaire à la place des nombres… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction de walsh