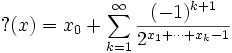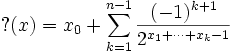Fonction Point D'interrogation

Fonction point d'interrogation

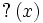La fonction point d'interrogation est, en mathématiques, une fonction, notée $?\left(x\right)$ .

Cette fonction fut définie par Hermann Minkowski en 1904 afin de créer une application continue de l'ensemble des nombres irrationnels quadratiques de l'intervalle $\left]0,1\right[$ vers l'ensemble des nombres rationnels dyadiques du même intervalle. La définition courante actuelle fut posée par Arnaud Denjoy en 1938.

Définition

Soit $x$ un nombre réel et $[x_0; x_1, x_2, \ldots]$ sa représentation en fraction continue. On pose :

${\rm ?}(x) = x_0 + \sum_{k=1}^\infty \frac {(-1)^{k+1}} {2^{x_1 + \cdots + x_k-1}}$

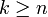Cette définition est légitime. Dans le cas d'un nombre irrationnel, la série converge toujours. Dans le cas d'un nombre rationnel, sa fonction continuée se limite à $[x_0; x_1, x_2, \ldots, x_n]$ et deux termes successifs de la série pour $k\ge n$ s'annnulent ; il est alors possible d'écrire :

${\rm ?}(x) = x_0 + \sum_{k=1}^{n-1} \frac {(-1)^{k+1}} {2^{x_1 + \cdots + x_k-1}}$

Exemples

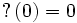
$?\left(0\right) = 0$
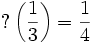
$\frac {1} {3} = \left[0;1,0,1,1\right]$ : $?\left(\frac {1} {3}\right) = \frac {1} {4}$
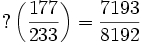
$\frac {177} {233} = \left[0;1,3,6,4,2\right]$ : $?\left(\frac {177} {233}\right) = \frac {7193} {8192}$
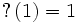
$?\left(1\right) = 1$
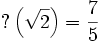
$\sqrt{2} = \left[1;2,2,\ldots\right]$ : $?\left(\sqrt{2}\right) = \frac {7} {5}$

Propriétés

La fonction point d'interrogation est strictement croissante.
Elle est absolument continue.
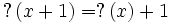
$?\left(x+1\right) = ?\left(x\right)+1$
Si $x$ est un nombre rationnel, 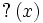$?\left(x\right)$ est un nombre rationnel dyadique.
Si $x$ est un nombre irrationnel quadratique, sa fraction continuée est périodique et 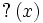$?\left(x\right)$ est un rationnel non-dyadique.
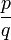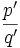Si $\frac {p} {q}$ et $\frac {p'} {q'}$ sont deux fractions irréductibles telles que 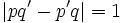$\left|pq'-p'q\right|=1$ (deux éléments successifs d'une suite de Farey),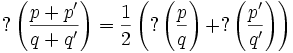 $?\left(\frac {p+p'} {q+q'}\right) = \frac {1} {2} \left(?\left(\frac{p}{q}\right) + ?\left(\frac{p'}{q'}\right) \right)$
La fonction point d'interrogation est un cas particulier des courbes fractales de de Rham.

Voir aussi

Liens internes

Théorie des nombres

Liens externes

(en) Minkowski's Question Mark Function (MathWorld)

Références

H. Minkowski, Verhandlungen des iii internationalen mathematiker-kongresses in heidelberg, (1904) Berlin.
A. Denjoy, Sur une fonction reelle de Minkowski, J. Math. Pures Appl. 17 (1938) p105-151.
Biblioni, L., Paradis, J., Viader, P., A New Light on Minkowski's ?(x) Function, Journal of Number Theory, 73 (1998), 212-227
Biblioni, L., Paradis, J., Viader, P., The Derivative of Minkowski's Singular Function, Journal of Mathematical Analysis and Applications, (2001) 107-125
Conley, Randolph M. A Survey of the Minkowski ?(x) Function, Master's Thesis, West Virginia University, (2003)
Vepstas, Linas, The Minkowski Question Mark and the Modular Group SL(2,Z), (2004)
Vepstas, Linas, Modular Fractal Measures, (2004).

Portail des mathématiques

Ce document provient de « Fonction point d%27interrogation ».

Catégorie : Fonction arithmétique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction Point D'interrogation de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Fonction point d'interrogation — de Minkowski. La fonction point d interrogation est, en mathématiques, une fonction, notée . Cette fonction fut définie par Hermann Minkowski en 1904 … Wikipédia en Français
Point d’interrogation — Point d interrogation ¿ ? Ponctuation Accolades ( { } ) · Parenthèses ( ( ) ) Chevrons ( < > ) · Crochets ( [ ] ) Guillemets ( « » ou… … Wikipédia en Français
Point d'interrogation — v · d · m … Wikipédia en Français
Interrogation — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. L interrogation est en linguistique un acte de langage par laquelle l émetteur d un énoncé adresse au destinataire (réel ou fictif) de celui ci une… … Wikipédia en Français
Point dironie — Point d ironie Pour l’article homonyme, voir Point d ironie (art contemporain). ؟ Ponctuation Accolades ( { } ) · Parenthèses ( ( ) ) Chevrons (& … Wikipédia en Français
Point d’exclamation — Point d exclamation ¡ ! Ponctuation Accolades ( { } ) · Parenthèses ( ( ) ) Chevrons ( < > ) · Crochets ( [ ] ) Guillemets ( « » ou… … Wikipédia en Français
Point d'arrêt (musique) — Point d orgue En solfège, on appelle point d orgue un signe en forme de point surmonté d un demi cercle, dont la fonction habituelle est de prolonger la durée de la figure de note ou de silence sur (ou sous) laquelle il est placé, ceci, au gré de … Wikipédia en Français
point — 1. point [ pwɛ̃ ] n. m. • 1175 « endroit, moment »; lat. punctum « piqûre », de pungere → poindre I ♦ A ♦ Portion de l espace déterminée avec précision. 1 ♦ Endroit, lieu. En divers, en plusieurs points. « il relevait la tête et fixait son regard … Encyclopédie Universelle
Point d'exclamation — v · d · m … Wikipédia en Français
Point d'ironie — Pour l’article homonyme, voir Point d ironie (art contemporain). v · d · … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction Point D'interrogation