- Fonction zeta d'hurwitz
-
Fonction zêta d'Hurwitz
En mathématiques, la fonction zêta d'Hurwitz est une des nombreuses fonctions zêta. Elle est définie comme suit :
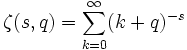 .
.
Elle s'étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre complexe q qui n'est pas entier négatif ou zéro.
Quand q = 1, ceci coïncide avec la fonction zêta de Riemann.
Sommaire
Relation avec les fonctions L de Dirichlet
En fixant un entier Q ≥ 1, les fonctions L de Dirichlet pour les caractères modulo Q sont des combinaisons linéaires, à coefficients constants, de
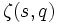 où q = r/Q et r = 1, 2, ..., Q. Ceci veut dire que les fonctions zêta d'Hurwitz pour un nombre rationnel q ont des propriétés analytiques qui sont étroitement liées à la classe des fonctions L.
où q = r/Q et r = 1, 2, ..., Q. Ceci veut dire que les fonctions zêta d'Hurwitz pour un nombre rationnel q ont des propriétés analytiques qui sont étroitement liées à la classe des fonctions L.Précisément, soit
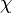 un caractère de Dirichlet mod Q. Alors, nous pouvons écrire la fonction L de Dirichlet sous la forme
un caractère de Dirichlet mod Q. Alors, nous pouvons écrire la fonction L de Dirichlet sous la forme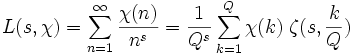 .
.
Formule d'Hurwitz
La formule d'Hurwitz est le théorème qui énonce
où
est une représentation de zêta qui est valide pour
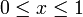 et s > 1. Ici,
et s > 1. Ici, 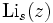 est la fonction polylogarithme.
est la fonction polylogarithme.Relation avec les polynômes de Bernoulli
La fonction β définie ci-dessus généralise les polynômes de Bernoulli :
où
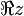 représente la partie réelle de z. De manière alternative,
représente la partie réelle de z. De manière alternative,Relation avec la fonction polygamma
La fonction zêta d'Hurwitz généralise la fonction polygamma :
Relation avec fonction transcendante de Lerch
La fonction transcendante de Lerch généralise la fonction zêta d'Hurwitz :
et ainsi
Équation fonctionnelle
L'équation fonctionnelle relie les valeurs de la fonction zêta sur le coté gauche -et droit- du plan complexe. Pour les nombres entiers
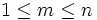 ,
,reste valable pour toutes les valeurs de s.
Série de Taylor
La dérivée partielle de la fonction zêta est une suite de Sheffer :
Ainsi, la série de Taylor peut être écrite comme suit :
Transformation de Fourier
La Transformée de Fourier discrète de la fonction zêta d'Hurwitz par rapport à l'ordre s est la fonction chi de Legendre.
Relation avec la fonction thêta de Jacobi
Si
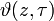 est la fonction thêta de Jacobi, alors
est la fonction thêta de Jacobi, alorsreste valable pour
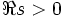 et z complexe, mais non pour un nombre entier. Pour z=n un entier, ceci se simplifie en
et z complexe, mais non pour un nombre entier. Pour z=n un entier, ceci se simplifie enoù
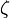 ici est la fonction zêta de Riemann. Cette distinction basée sur z tient compte du fait que la fonction thêta de Jacobi converge vers la Fonction δ de Dirac pour z lorsque
ici est la fonction zêta de Riemann. Cette distinction basée sur z tient compte du fait que la fonction thêta de Jacobi converge vers la Fonction δ de Dirac pour z lorsque 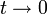 .
.Bien que la fonction zêta d'Hurwitz est vue par les mathématiciens comme relevant de la plus pure discipline des mathématiques, la théorie des nombres, elle apparaît aussi dans les statistiques appliquées ; voir la loi de Zipf et la loi de Zipf-Mandelbrot.
Références
- Tom M. Apostol Introduction to Analytic Number Theory, (1976) Springer-Verlag, New York. ISBN 0-387-90163-9 (voir le chapitre 12)
- Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4 . Voir le paragraphe 6.4.10.
- Djurdje Cvijovic and Jacek Klinowski. Math. Comp. 68 (1999), 1623-1630, 1999. (abstrait, en anglais)
- Linas Vepstas, L'opérateur de Bernoulli, l'opérateur de Gauss-Kuzmin-Wirsing, et la fonction zêta de Riemann (en anglais).
- Portail des mathématiques
Catégories : Fonction zêta | Statistiques | Fonctions spéciales
Wikimedia Foundation. 2010.

![\zeta(1-s,x)=\frac{1}{2s}\left[e^{-i\pi s/2}\beta(x;s) + e^{i\pi s/2} \beta(1-x;s) \right]](/pictures/frwiki/48/08afc1b3685447f4fb7149c56ed8fd3f.png)
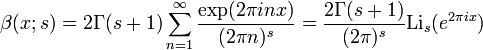
![B_n(x) = -\Re \left[ (-i)^n \beta(x;n) \right]](/pictures/frwiki/102/fb05d128593f55353729151788e95b0b.png)
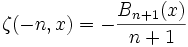
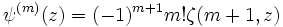
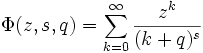
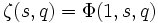
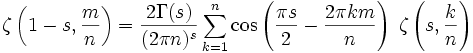
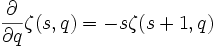
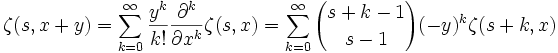
![\int_0^\infty \left[\vartheta (z,it) -1 \right] t^{s/2} \frac{dt}{t}=
\pi^{-(1-s)/2} \Gamma \left( \frac {1-s}{2} \right)
\left[ \zeta(1-s,z) + \zeta(1-s,1-z) \right]\,](/pictures/frwiki/54/63a45442e9b287d065b92b8d9109c9d4.png)
![\int_0^\infty \left[\vartheta (n,it) -1 \right] t^{s/2} \frac{dt}{t}=
2\ \pi^{-(1-s)/2} \ \Gamma \left( \frac {1-s}{2} \right) \zeta(1-s)
=2\ \pi^{-s/2} \ \Gamma \left( \frac {s}{2} \right) \zeta(s)\,](/pictures/frwiki/101/e1ba7ba3d5f1646239a63cd390c48661.png)