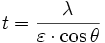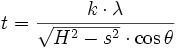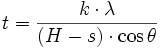Loi de Scherrer

Loi de Scherrer

Formule de Scherrer

Page d'aide sur l'homonymie Pour les articles homonymes, voir Scherrer.

La formule de Scherrer, ou relation de Laue-Scherrer, est une formule utilisée en diffraction X sur des poudres ou échantillons polycristallins. Elle relie la largeur des pics de diffraction — ou des anneaux de Debye-Scherrer — à la taille des cristallites.

Si t est la taille du cristallite (son diamètre si on l'estime sphérique), ε est la largeur intégrale d'un pic, λ est la longueur d'onde de l'onde incidente et θ est la moitié de la déviation de l'onde (la moitié de la position du pic sur le diagramme), alors la formule de Scherrer s'écrit :

t = \frac{\lambda}{\varepsilon \cdot \cos \theta}

En pratique, on utilise souvent la largeur à mi-hauteur H du pic ; il faut donc corriger la largeur par un facteur k. Par ailleurs, même avec un cristallite « infini », on aurait une largeur s due aux défauts de l'optique instrumentale. On utilise donc la formule

t = \frac{k \cdot \lambda}{\sqrt{H^2 - s^2} \cdot \cos \theta}

k prend en général la valeur 0,89. On utilise fréquemment la formule approchée

t = \frac{k \cdot \lambda}{(H - s) \cdot \cos \theta}

L'élargissement commence à être visible pour des cristallites faisant moins de 1 µm.

Sommaire

Principe

En condition de diffraction (voir l'article Loi de Bragg), les rayons X diffusés par chaque nœud du réseau — atome ou molécule — sont en phase et produisent une interférence constructive. Si l'on s'écarte légèrement des conditions de diffraction, l'onde diffusée par un nœud sera en opposition de phase avec l'onde diffusée par un autre nœud ; les nœuds dont les ondes s'annulent seront d'autant plus éloignés que le déphasage entre chaque nœud est faible, donc que l'on est proche des conditions de diffraction.

Le cristallite étant de taille finie, si l'on est très proche des conditions de diffraction, alors la distance entre les nœuds dont les ondes s'annulent est supérieure à la taille du cristallite. On a donc de l'intensité là où il ne devrait y avoir que la ligne de fond.

Ce phénomène explique la largeur du pic induite par l'échantillon.

Voir aussi l'article Réseau de diffraction optique > Largeur des raies et taille du réseau

Limites de la méthode

Les cristallites n'ont pas tous la même taille. On a en fait une distribution de tailles.

Dans le cas d'une distribution unimodale, il faut au moins deux paramètres pour décrire cette distribution : la moyenne et la largeur. Or, la formule de Scherrer ne donne qu'une seule valeur. Correspond elle à l'espérance mathématique ? À la médiane ? Au maximum de la distribution (mode) ?

La formule de Scherrer sert de fait plus pour du qualitatif — comparer des échantillons entre eux, avoir un critère de sélection — que pour du quantitatif strict.

La notion de taille de cristallite est distincte de celle granulométrie : un grain de poudre peut être composé de plusieurs cristallites.

Voir aussi

Bibliographie

  • J.-P. Eberhart, Méthodes physiques d'étude des minéraux et des matériaux solides, éd. Doin Éditeurs (Paris), 1976, pp 225–227
  • B. D. Cullity, Elements of X-Ray Diffraction, éd. Addison-Wesley Publishing Co, 1956, pp 98–99
  • R. Jenkins, R. L. Snyder, X-Ray Powder Diffractometry, éd. Wiley -Interscience, 1996, pp 89–91

Articles connexes

  • Portail de la physique Portail de la physique
Ce document provient de « Formule de Scherrer ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi de Scherrer de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Formule De Scherrer — Pour les articles homonymes, voir Scherrer. La formule de Scherrer, ou relation de Laue Scherrer, est une formule utilisée en diffraction X sur des poudres ou échantillons polycristallins. Elle relie la largeur des pics de diffraction ou des… …   Wikipédia en Français

  • Formule de scherrer — Pour les articles homonymes, voir Scherrer. La formule de Scherrer, ou relation de Laue Scherrer, est une formule utilisée en diffraction X sur des poudres ou échantillons polycristallins. Elle relie la largeur des pics de diffraction ou des… …   Wikipédia en Français

  • Méthode de Scherrer — Formule de Scherrer Pour les articles homonymes, voir Scherrer. La formule de Scherrer, ou relation de Laue Scherrer, est une formule utilisée en diffraction X sur des poudres ou échantillons polycristallins. Elle relie la largeur des pics de… …   Wikipédia en Français

  • Fonction De Voigt — Une fonction de Voigt est le produit de convolution d une fonction gaussienne et d une fonction lorentzienne ayant le même sommet. C est donc une fonction de la forme soit, si le sommet se trouve en 0 (x0 = 0)  …   Wikipédia en Français

  • Fonction de voigt — Une fonction de Voigt est le produit de convolution d une fonction gaussienne et d une fonction lorentzienne ayant le même sommet. C est donc une fonction de la forme soit, si le sommet se trouve en 0 (x0 = 0)  …   Wikipédia en Français

  • Pseudo-fonction de Voigt — Fonction de Voigt Une fonction de Voigt est le produit de convolution d une fonction gaussienne et d une fonction lorentzienne ayant le même sommet. C est donc une fonction de la forme soit, si le sommet se trouve en 0 (x0 = 0)  …   Wikipédia en Français

  • Pseudo fonction de Voigt — Fonction de Voigt Une fonction de Voigt est le produit de convolution d une fonction gaussienne et d une fonction lorentzienne ayant le même sommet. C est donc une fonction de la forme soit, si le sommet se trouve en 0 (x0 = 0)  …   Wikipédia en Français

  • Courbe de Lorentz — Fonction lorentzienne On reconnaît une courbe lorentzienne à la forme suivante : C est l expression la plus simple d une lorentzienne, centrée en x=0. Une forme paramétrée par l abscisse x0 du sommet et la largeur Γ à mi hauteur (couramment… …   Wikipédia en Français

  • Fonction Lorentzienne — On reconnaît une courbe lorentzienne à la forme suivante : C est l expression la plus simple d une lorentzienne, centrée en x=0. Une forme paramétrée par l abscisse x0 du sommet et la largeur Γ à mi hauteur (couramment appelée largeur de la… …   Wikipédia en Français

  • Fonction lorentzienne —  Pour l’article homonyme, voir Courbe de Lorenz.  On reconnaît une courbe lorentzienne à la forme suivante : C est l expression la plus simple d une lorentzienne, centrée en x=0. Une forme paramétrée par l abscisse x0 du sommet et… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”