- Fonction de Pearson VII
-
Fonction de Pearson
Les fonctions de Pearson ont été crées pour représenter des distributions unimodales. Il en existe douze. Elles ont été inventées par Karl Pearson à la fin du XIXe siècle et au début du XXe siècle.
Sommaire
Pearson IV
La densité de probabilité ƒ, pour x réel, vaut :
où
- m, ν, a et λ sont des réels ;
- m > 1/2 ;
- k est un facteur de normalisation.
La fonction est invariante si l'on change simultanément le signe de a et de ν, on prend donc par convention
- a > 0.
Si m ≤ 1/2, la fonction n'est pas normalisable.
La fonction de Pearson IV est en fait une version asymétrique de la loi de Student ; de fait, on retrouve la loi de Student avec 2m-1 degrés de liberté pour ν = 0.
Pour m = 1, la distribution de Pearson IV est une forme asymétrique de la distribution de Cauchy (ou distribution de Breit-Wigner).
La fonction a un mode (sommet) unique placé en
elle présente deux points d'inflexion situés en
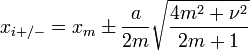 .
.
Sa moyenne vaut
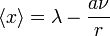 pour m > 1
pour m > 1
en posant
- r = 2(m - 1).
La moyenne est infinie si ν = 0 et m ≤ 1.
Sa variance vaut
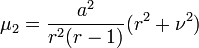 pour m > 3/2.
pour m > 3/2.
La variance est infinie si m ≤ 3/2.
Le facteur de normalisation vaut :
où Γ est la fonction Gamma d'Euler.
Pearson VII
La VIIe fonction de Pearson est définie, pour x entier, par
où M est le paramètre de forme, ou « largeur de Pearson ».
On écrit parfois une expression simplifiée :
On a
- M < 1 : distribution dit super lorentzien ;
- M = 1 : distribution de Cauchy : Lorentz (lorentzienne) : Breit-Wigner ;
- M = ∞ : distribution de Gauss-Laplace (gaussienne, loi normale).
Elle est utiilsée en radiocristallographie pour modéliser le profil des pics de diffraction (voir aussi Fonction de Voigt).
Voir aussi
Bibliographie
- Karl Pearson, Contributions to the Mathematical Theory of Evolution.—II. Skew Variation in Homogeneous Material, Philosophical Transactions of the Royal Society of London A, 186, (1895), page 343.
- Karl Pearson, Mathematical Contributions to the Theory of Evolution.—X. Supplement to a Memoir on Skew Variation, Philosophical Transactions of the Royal Society of London A, 197, (1901), page 443.
- Karl Pearson, Mathematical Contributions to the Theory of Evolution.—XIX. Second Supplement to a Memoir on Skew Variation, Philosophical Transactions of the Royal Society of London A, 216, (1916), page 429.
Liens externes
- (en) A Guide to the Pearson Type IV Distribution, Joel Heinrich, University of Pennsylvania, 2004
- Portail des probabilités et des statistiques
Catégories : Fonction remarquable | Loi de probabilité
Wikimedia Foundation. 2010.

![f(x) = k \cdot \left [ 1 + \left ( \frac{x - \lambda}{a}\right )^2 \right ]^{-m} \cdot \exp \left [ - \nu \cdot \tan^{-1} \left ( \frac{x - \lambda}{a}\right ) \right ]](/pictures/frwiki/101/ef8f411df4d64a6773e825a84aa73cda.png)
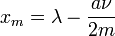
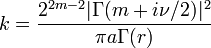
![f = \frac{1}{\left [ 1+ \left (\frac{2(x-x_0) \cdot \sqrt{2^{1/M}-1}}{w} \right )^2 \right ]^M}](/pictures/frwiki/98/bfa0784b36215fdb46a8d4807186c5ac.png)
![f = \left [ 1 + K^2 \frac{(x-x_0)^2}{M} \right ]^{-M}](/pictures/frwiki/52/44245cb5f95a7e898347bf9e403ec53c.png)