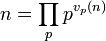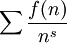Fonction faiblement multiplicative

Fonction multiplicative

En arithmétique, une fonction multiplicative est une fonction arithmétique f de l'ensemble des entiers naturels non nuls dans lui-même vérifiant les deux conditions suivantes :

f(1)=1 ;
Pour tous entiers premiers entre eux a et b, on a : f (a.b) = f(a).f (b).

Une fonction complètement multiplicative est une fonction arithmétique g vérifiant :

g(1)=1 ;
Pour tous entiers a et b quelconques, on a : g(a.b)=g(a).g(b).

Ces dénominations peuvent varier d'un ouvrage à un autre : fonction faiblement multiplicative pour fonction multiplicative, fonction multiplicative pour fonction complètement multiplicative.

Les fonctions multiplicatives interviennent notamment en théorie analytique des nombres, dans les séries de Dirichlet.

Sommaire

1 Détermination et exemples
- 1.1 Exemples
2 Séries de Dirichlet
- 2.1 Produit de convolution
- 2.2 Anneau de Dirichlet
3 Voir aussi
4 Références
- 4.1 Ouvrages
- 4.2 Notes et références

Détermination et exemples

Une fonction multiplicative f est entièrement déterminée par les valeurs de f en les puissances des entiers premiers. En effet, d'après le théorème fondamental de l'arithmétique, tout entier naturel s'écrit comme produit de facteurs premiers, unique à permutation des termes près. Si n est un entier, on a :

$n=\prod_p p^{v_p(n)}$

où l'entier v_p(n) est uniquement déterminé par n et s'appelle la valuation p-adique de n. En appliquant f, il vient :

$f(n)=\prod_p f\left[p^{v_p(n)}\right]$ .

Il n'existe aucune contrainte supplémentaire : toute suite d'entiers indexées par les puissances des entiers premiers donne, via la formule ci-dessus, une unique fonction multiplicative.

Pour des raisons analogues, une fonction complètement multiplicative g est entièrement déterminée par ses valeurs en les nombres premiers. En reprenant les notations ci-dessus :

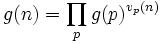$g(n)=\prod_p g(p)^{v_p(n)}$ .

Ces considérations prouvent qu'il existe une infinité de fonctions multiplicatives.

En général, si f est une fonction multiplicative et si a, b sont deux nombres entiers naturels non nuls quelconques, alors on a :

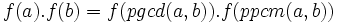$f(a).f(b)=f(pgcd(a,b)).f(ppcm(a,b))\,$ ,

où pgcd est le plus grand commun diviseur et ppcm est le plus petit commun multiple des entiers.

Exemples

La liste suivante fournit des fonctions multiplicatives dont l'intérêt est historique et/ou théorique :

φ : la fonction φ d'Euler, qui associe à tout entier positif n le nombre d'entiers naturels premiers avec n et inférieurs à cet entier naturel,
μ : la fonction de Möbius, relative au nombre de facteurs premiers des entiers sans carré,
n↦pgcd(n,m) : qui à l'entier n associe le plus grand commun diviseur des entiers m et n, m étant fixé,
d : qui associe à un entier naturel n, le nombre de diviseurs positifs de n,
σ : qui associe à un entier n la somme de tous les diviseurs positifs de n,
σ_k : qui associe à un entier n, la somme des puissances k-ièmes de tous les diviseurs positifs de n (où k peut être un nombre complexe quelconque). Dans les cas particuliers suivants nous avons
- σ₀(n) = d(n) et
- σ₁(n) = σ(n),
1 : la fonction constante, définie par 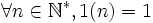$\forall n\in\mathbb{N}^*, 1(n) = 1$ (complètement multiplicative)
Id : l'application identité, définie par 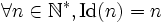$\forall n\in\mathbb{N}^*, \operatorname{Id}(n) = n$ (complètement multiplicative)
Id_k : la fonction puissance, définie par 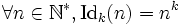, où k est un entier naturel (ou éventuellement un nombre complexe) (complètement multiplicative). Nous avons les cas particuliers suivants
- Id₀(n) = 1(n) et
- Id₁(n) = Id(n),
ε : la fonction définie par, ε(1) = 1 et pour tout entier naturel n>1, ε(n)= 0, parfois appelée élément neutre pour le produit de convolution de Dirichlet (complètement multiplicative).
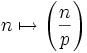$n\mapsto\left(\frac{n}{p}\right)$ , l'application qui associe à un entier naturel n, le symbole de Legendre de n et p, où p est un nombre premier fixé (complètement multiplicative),
λ : la fonction de Liouville, relative au nombre de facteurs premiers divisant un entier naturel n (complètement multiplicative).
γ : définie par 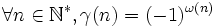$\forall n\in\mathbb{N}^*, \gamma(n)=(-1)^{\omega(n)}$ , où la fonction additive ω associe à un entier naturel n le nombre de nombres premiers distincts divisant n,
Tous les caractères de Dirichlet sont des fonctions complètement multiplicatives.

Explications

Un exemple d'une fonction non multiplicative est la fonction arithmétique r₂ qui à un entier n, associe le nombre de décompositions de n sous la forme d'une somme de deux carrés de nombres entiers positifs, négatifs ou nuls, en tenant compte de l'ordre dans les écritures. Par exemple

1 = 1² + 0² = (-1)² + 0² = 0² + 1² = 0² + (-1)²

et donc r₂(1)=4≠1. Ceci prouve que la fonction n'est pas multiplicative. Cependant, 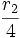$\frac{r_2}{4}$ est multiplicative.

Séries de Dirichlet

Produit de convolution

Si f et g sont deux fonctions multiplicatives, on définit une nouvelle fonction multiplicative f * g, appelée convolution de Dirichlet de f et g, comme suit :

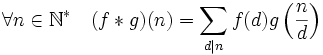$\forall n\in\mathbb{N}^*\quad (f*g)(n)=\sum_{d|n}f(d)g\left(\frac{n}{d}\right)$ ,

où la somme portant sur tous les diviseurs positifs d de n.

En effet, introduisons n et m deux entiers premiers entre eux. Leurs décompositions en facteurs premiers ne comportent aucun nombre premier commun. Si d est un diviseur de n.m, alors tout diviseur premier p de d divise n.m et donc par le lemme d'Euclide ou bien n ou bien m. Par regroupement de facteurs premiers, l'entier d s'écrit de manière unique d=d₁.d₂ comme produit de deux nombres entiers premiers d₁ etd₂ divisant respectivement n et m. Par définition :

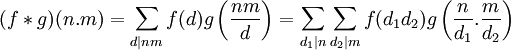$(f*g)(n.m)=\sum_{d|nm}f(d)g\left(\frac{nm}{d}\right)=\sum_{d_1|n}\sum_{d_2|m}f(d_1d_2)g\left(\frac{n}{d_1}.\frac{m}{d_2}\right)$ .

Or, comme f et g sont elles-mêmes supposées multiplicatives :

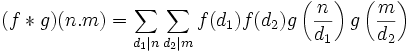$(f*g)(n.m)=\sum_{d_1|n}\sum_{d_2|m}f(d_1)f(d_2)g\left(\frac{n}{d_1}\right)g\left(\frac{m}{d_2}\right)$ ,

$(f*g)(n.m)=\left[\sum_{d_1|n}f(d_1)g\left(\frac{n}{d_1}\right)\right].\left[\sum_{d_2|m}f(d_2)g\left(\frac{m}{d_2}\right)\right]$ ,

(f * g)(n . m) = (f * g)(n).(f * g)(m)

C'est précisément l'égalité attendue.

Avec cette opération, l'ensemble de toutes les fonctions multiplicatives se transforme en groupe abélien; l'élément neutre est $ε$ .

Les relations les plus importantes vérifiées par les fonctions multiplicatives listées ci-dessus sont :

$ε$ = $μ$ * 1 (la formule d'inversion de Möbius)
$φ$ = $μ$ * Id
d = 1 * 1
$σ$ = Id * 1 = $φ$ * d
$σ$ _k = Id_k * 1
Id = $φ$ * 1 = $σ$ * $μ$
Id_k = $σ$ _k * $μ$

Anneau de Dirichlet

La convolution de Dirichlet peut être définie pour des fonctions arithmétiques générales, et leur confère une structure d'anneau, l'anneau de Dirichlet.

Formellement, à une fonction arithmétique f est associée une série formelle :

$\sum \frac{f(n)}{n^s}$

Pour une fonction complètement multiplicative :

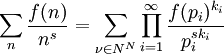
$\sum_n \frac{f(n)}{n^s}=\sum_{\nu\in N^N}\prod_{i=1}^{\infty}\frac{f(p_i)^{k_i}}{p_i^{sk_i}}$

$\sum_n \frac{f(n)}{n^s}=\prod_{i=1}^{\infty}\sum_{k=0}^{\infty}{\left[\frac{f(p)}{p^s}\right]}^s$ .

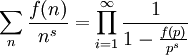
$\sum_n \frac{f(n)}{n^s}=\prod_{i=1}^{\infty}\frac{1}{1-\frac{f(p)}{p^s}}$

Voir aussi

Références

Ouvrages

Notes et références

Portail des mathématiques

Ce document provient de « Fonction multiplicative ».

Catégorie : Fonction arithmétique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction faiblement multiplicative de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Fonction complètement multiplicative — Fonction multiplicative En arithmétique, une fonction multiplicative est une fonction arithmétique f de l ensemble des entiers naturels non nuls dans lui même vérifiant les deux conditions suivantes : f(1)=1 ; Pour tous entiers premiers … Wikipédia en Français
Fonction strictement multiplicative — Fonction multiplicative En arithmétique, une fonction multiplicative est une fonction arithmétique f de l ensemble des entiers naturels non nuls dans lui même vérifiant les deux conditions suivantes : f(1)=1 ; Pour tous entiers premiers … Wikipédia en Français
Fonction Multiplicative — En arithmétique, une fonction multiplicative est une fonction arithmétique f de l ensemble des entiers naturels non nuls dans lui même vérifiant les deux conditions suivantes : f(1)=1 ; Pour tous entiers premiers entre eux a et b, on… … Wikipédia en Français
Fonction multiplicative — En arithmétique, une fonction multiplicative est une fonction arithmétique f de l ensemble des entiers naturels non nuls dans lui même vérifiant les deux conditions suivantes : f(1)=1 ; Pour tous entiers premiers entre eux a et b, on… … Wikipédia en Français
Nepenthes rajah — ██████████70 … Wikipédia en Français
Nepenthes Rajah — ██████████ … Wikipédia en Français
Nepenthes rajah — ██████████ … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction faiblement multiplicative

Fonction multiplicative

Sommaire