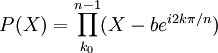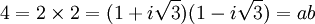- Factorisation des polynomes
-
Factorisation des polynômes
La factorisation d'un polynôme consiste à écrire celui-ci comme produit de polynômes. Les factorisations intéressantes sont celles permettant d'écrire le polynôme initial en produit de polynômes dont le degré serait inférieur au degré du polynôme de départ. Un polynôme pour lequel aucune factorisation de ce type n'existe s'appelle un polynôme irréductible.
La décomposition d'un polynôme en produits de polynômes irréductibles existe, et a une propriété d'unicité (à un facteur inversible près), pour tout polynôme à coefficients réels ou complexes. Ceci est encore vrai lorsque les coefficients sont dans un anneau factoriel, que le polynôme soit à une ou plusieurs indéterminées. Cette propriété est, pour l'ensemble des polynômes, analogue au théorème fondamental de l'arithmétique pour l'ensemble des entiers.
La recherche d'une factorisation est un problème algorithmique de difficulté variable suivant, en premier lieu, l'anneau de coefficients considéré, et en second lieu, la taille de ces coefficients et le degré du polynôme.
La factorisation d'un polynôme est utile pour réduire une fonction rationnelle en éléments simples.
Sommaire
Polynômes à coefficients réels ou complexes
Polynômes à coefficients réels
Méthodes élémentaires
Les identités remarquables et la propriété de distributivité de la multiplication sur l'addition fournissent des méthodes élémentaires de factorisation de polynômes
Exemples
- 3x2 + 9 = 3(x2 + 3)
- 4x2 − 8x = 4x(x − 2)
- x2 + 2ax + a2 = (x + a)2
- x2 − b2 = (x − b)(x + b)
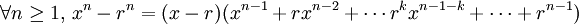
La première des factorisations ne décompose pas le polynôme en produit de polynômes de degré moindre. Cependant, elle offre l'avantage de présenter un polynôme dont le coefficient du terme de plus haut degré est 1. De tels polynômes sont dits unitaires et sont utilisés dans les décompositions pour garantir l'unicité de celles-ci.
La dernière factorisation offre un moyen de prouver que tout polynôme P possédant r comme racine peut s'écrire
- P(x) = (x − r)Q(x)
où Q est de degré inférieur au degré de P.
DémonstrationL'identité remarquable précédente affirme que
où pk est un polynôme de degré k-1
Soit alors P le polynôme
Puisque r est une racine de P, on a P(r)=0, donc
Cependant, en pratique, quand une racine r est connue, la factorisation précédente se calcule plutôt en utilisant une division de polynome ou la méthode de Hörner.
Polynômes irréductibles
Les polynômes irréductibles dans
 sont les polynômes qui ne peuvent pas se décomposer en produit de deux polynômes de degrés supérieurs ou égaux à un. En particulier, les polynômes de degré 1 sont donc irréductibles.
sont les polynômes qui ne peuvent pas se décomposer en produit de deux polynômes de degrés supérieurs ou égaux à un. En particulier, les polynômes de degré 1 sont donc irréductibles.Un polynôme de degré 2 qui pourrait s'écrire comme produit de polynômes de degré 1 possèderait des racines réelles. Par contraposée, un polynôme de degré 2 ne possédant pas de racine réelle est irréductible. C'est le cas de tous les polynômes de degré 2 dont le discriminant est négatif.
On démontre que les seuls polynômes à coefficient réels sont de ce type (polynômes de degré 1 ou polynome de degré 2 dont le discriminant est négatif). Ce résultat est en général vu comme une conséquence du théorème de d'Alembert-Gauss, qui porte sur les polynômes à coefficients complexes.
Ainsi le polynôme
- P(x) = x4 + 4
qui ne semble pas factorisable de manière simple et ne possède pas de racine n'est pas irréductible.
- P(x) = x4 + 4x2 + 4 − 4x2 = (x2 + 2)2 − (2x)2 = (x2 − 2x + 2)(x2 + 2x + 2)
Ce même théorème de D'alembert Gauss permet aussi de prouver que tout polynôme P à coefficients réels possède une décomposition unique (à l'ordre près) de la forme suivante:
où lespi sont des polynômes irréductibles unitaire (le coefficient du terme de plus haut degré est 1) de degré 2.
Racines et factorisation
Articles détaillés : algorithme de recherche d'un zéro d'une fonction et équation polynomiale.Le lien existant entre les racines d'un polynôme et sa factorisation justifie les études portant sur ses racines. Les recherches s'orientent dans deux directions : recherche de racines exactes éventuellement par incursion dans les complexes et recherche de racines approchées.
La première voie a conduit à l'étude des coefficients des polynômes, qui d'après le théorème de Viète, s'expriment comme polynômes symétriques des racines. Cette voie de recherche, fructueuse sur les polynômes de degré 3 et 4, et sur certains polynômes de degré supérieur a laissé croire qu'il serait possible de déterminer toutes les racines d'un polynôme en utilisant seulement des opérations de somme, produit, quotient et extraction de racine nième, quitte à passer par les complexes. Si les racines d'un polynôme s'écrivent effectivement ainsi, on dit qu'il est résoluble par radicaux. Dans le courant du XIXe siècle, Niels Henrik Abel démontre que les équations polynomiales de degré supérieur ou égal à 5 ne sont pas toutes résolubles par radicaux (théorème d'Abel). Une classification des équations résolubles par radicaux est donnée par la théorie de Galois.
La seconde voie est la recherche de racines approchées de polynômes. Ce sont les algorithme de recherche d'un zéro d'une fonction dont un des classiques est la méthode de Newton. Ces méthodes nécessitent de déterminer combien de racines se trouvent dans un intervalle donné. Descartes par sa règle des signes permet de déterminer le nombre de changements de signe d'un polynôme en observant seulement le signe de ses coefficients et par la même le nombre de racines. Le théorème de Sturm permet de déterminer le nombre de racines dans un intervalle donné d'un polynôme ne comportant que des racines simples. Il permet aussi de séparer les racines dans des intervalles distincts.
Polynômes à coefficients complexes
Comme il est indiqué dans la section précédente, la recherche des polynômes irréductibles à coefficients réels et la factorisation des polynômes nécessite une incursion dans les complexes où les factorisations ont une présentation simple.
Dans l'ensemble des complexes les seuls polynômes irréductibles sont les polynômes de degré 1 et tout polynome P complexe de degré n se décompose de manière unique sous la forme suivante :
avec
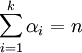
La racine ri est dite d'ordre αi.
Mais les mêmes difficultés persistent sur la mise en place effective d'une factorisation.
DémonstrationsA compléter
Soit
![P\in\R[X]](/pictures/frwiki/49/1b2cb956c776020d36d4786301a51be0.png) un polynôme irréductible de degré supérieur ou égal à 2.
un polynôme irréductible de degré supérieur ou égal à 2.P n'admet pas de racines dans
 , mais comme
, mais comme ![P\in\mathbb{C}[X]](/pictures/frwiki/50/20f56686c6eaf7e0841ad88aa8362f26.png) , P admet une racine α dans
, P admet une racine α dans  . De plus P étant irréductible dans
. De plus P étant irréductible dans ![\R[X]](/pictures/frwiki/54/60ed190117e7614d227f8d1693161a5b.png) ,
, 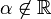 .
.Il existe donc
![Q\in\mathbb{C}[X]](/pictures/frwiki/102/f364354592a3f4a4dd5f73a854cec169.png) tel que P = (X − α)Q.
tel que P = (X − α)Q.Dans
![\mathbb{C}[X]](/pictures/frwiki/54/6ddcc166f3aa1cea808fa816f33ec673.png) , le conjugé de P est
, le conjugé de P est 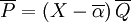 . Mais comme
. Mais comme ![P\in\R[X]](/pictures/frwiki/49/1b2cb956c776020d36d4786301a51be0.png) ,
, 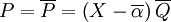 . Donc
. Donc 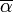 est une racine de P.
est une racine de P.Comme
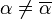 , P est divisible par
, P est divisible par ![\left(X-\alpha\right)\left(X-\overline{\alpha}\right) = X^2- (\alpha +\overline{\alpha})X+ \alpha\overline{\alpha} \in\R[X]](/pictures/frwiki/55/7c9228d67a1b8409a65882adbaa9b3fe.png) .
.Comme P est irréductible
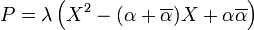 avec
avec 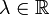 .
.Ainsi P est de degré 2, il n'y a donc pas de polynôme irréductible de degré supérieur ou égal à 3 dans
![\R[X]](/pictures/frwiki/54/60ed190117e7614d227f8d1693161a5b.png) .
.Exemples
Considérons le polynôme
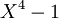 à coefficients dans
à coefficients dans 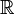 ou
ou  .
.- L'identité remarquable
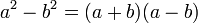 donne :
donne :
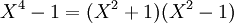
- puis :
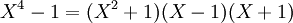 .
.- Ceci est la factorisation en produit de facteurs irréductibles à coefficients dans
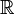 .
.
Ainsi,on a le signe de
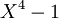 en fonction de X (réel, bien entendu) :
en fonction de X (réel, bien entendu) :X<-1 ou X>1 => P(X)>0
-1<X<1 => P(X) <0
- La factorisation en produit de facteurs irréductibles à coefficients dans
 est :
est :
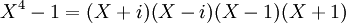 .
.
Plus généralement, on sait factoriser dans
 puis dans
puis dans  , tout polynôme P de la forme Xn − a où a > 0. Si on note
, tout polynôme P de la forme Xn − a où a > 0. Si on noteles racines de P sont :
- rk = bei2kπ / n
et P a pour décomposition dans
 :
:La décomposition dans
 consiste à regrouper les racines conjuguées. La décomposition est différente selon que n est pair ou impair est différente
consiste à regrouper les racines conjuguées. La décomposition est différente selon que n est pair ou impair est différenteA compléter
Polynômes à coefficients dans un anneau
Lorsque les coefficients ne sont pas réels ou complexes, les polynômes irréductibles peuvent être de degré supérieur à 2 et il n'y a parfois pas unicité de la factorisation.
Polynômes irréductibles
On appelle polynôme irréductible tout polynôme de degré supérieur ou égal à un dont les seuls diviseurs sont les polynômes de degré nul ou les polynômes associés. En d'autres termes
- P est irréductible ssi
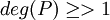 et
et ![\forall (Q,R) \in A[X]^2 \quad P=QR \Rightarrow deg(Q)=0 \or deg(R)=0](/pictures/frwiki/56/83fd70133b89d12db2f8b496c983ad31.png)
Dans un anneau intègre, les résultats suivants sont immédiats :
- Tout polynôme de degré un est irréductible
-
- mais ce n'est pas le cas dans un anneau quelconque. en effet dans
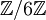 , P(x) = 5x + 1 = (2x + 1)(3x + 1)
, P(x) = 5x + 1 = (2x + 1)(3x + 1)
- mais ce n'est pas le cas dans un anneau quelconque. en effet dans
- Tout polynôme de degré deux est irréductible s'il ne possède pas de racine
Des polynômes réductibles dans
 peuvent se révéler irréductible dans
peuvent se révéler irréductible dans  :
:- p(x) = x2 − 2 est réductible dans
 mais non réductible dans
mais non réductible dans 
Le lemme de Gauss permet d'affirmer que tout polynôme de
![\Z[X]](/pictures/frwiki/100/dba144b0c7e9c5c01ae1a1d569bfea39.png) irréductible dans
irréductible dans ![\Z[X]](/pictures/frwiki/100/dba144b0c7e9c5c01ae1a1d569bfea39.png) l'est aussi dans
l'est aussi dans ![\mathbb Q[X]](/pictures/frwiki/57/9918bced8e53444100ccab7a8a59f47d.png)
Le critère d'Eisenstein fournit une condition suffisante pour qu'un polynôme de
![\Z[X]](/pictures/frwiki/100/dba144b0c7e9c5c01ae1a1d569bfea39.png) soit irréductible : il suffit de trouver un nombre premier divisant tous les coefficients de P sauf le coefficient de terme de plus haut degré et tel que p2 ne divise pas le terme constant. Ainsi
soit irréductible : il suffit de trouver un nombre premier divisant tous les coefficients de P sauf le coefficient de terme de plus haut degré et tel que p2 ne divise pas le terme constant. Ainsi- P(x) = x4 − 9x3 + 3x2 − 6x + 15 est irréductible dans
![\Z[X]](/pictures/frwiki/100/dba144b0c7e9c5c01ae1a1d569bfea39.png) car 3 divise tous les coefficients sauf celui du terme de degré 4 et que 9 ne divise pas 15.
car 3 divise tous les coefficients sauf celui du terme de degré 4 et que 9 ne divise pas 15.
Factorisation
Article détaillé : anneau factoriel.Dans un anneau intègre, l'existence d'une décomposition d'un polynôme non constant en produit de polynômes irréductibles est une conséquence immédiate de la définition d'un polynôme irréductible. Une récurrence forte le prouve aisément : les polynômes de degré 1 sont irréductibles. On suppose que tout polynôme de degré strictement inférieur à n est irréductible ou décomposable en produit de polynômes irréductibles. Soit alors P un polynôme de degré n, il est soit irréductible soit décomposable en produit de deux polynomes de degré strictement inférieurs à n eux-mêmes produits de polynômes irréductibles.
Cependant l'unicité de la décomposition à un facteur inversible près, n'est vraie que sur les anneaux factoriels. Et il n'est pas toujours possible de le décomposer en produit de polynômes unitaires multiplié par une constante.
- P(x) = 6x2 − 5x + 1 = (2x − 1)(3x − 1) = (1 − 2x)(1 − 3x)
est une décomposition unique à un facteur inversible près (-1) ne pouvant pas comporter de polynôme unitaire.
Dans un anneau qui ne serait pas factoriel, par exemple
![\Z[i\sqrt 3]](/pictures/frwiki/102/f366dc9613ed91e534caea0ea06991eb.png) , on peut trouver des polynômes ayant des décomposition différentes : en remarquant que
, on peut trouver des polynômes ayant des décomposition différentes : en remarquant queOn peut écrire
- P(x) = 4x2 − 4 = (2x − 2)(2x + 2) = (ax − a)(bx + b)
qui donne deux décompositions différentes même à un facteur inversible près.
Un corps étant un exemple d'anneau factoriel, tout polynôme non constant de
![\mathbb K[X]](/pictures/frwiki/49/11cf18672fa8c102e5d2ec8bdfe203c8.png) possède une décomposition unique sous forme de produit de polynômes unitaires irréductibles multiplié par une constante.
possède une décomposition unique sous forme de produit de polynômes unitaires irréductibles multiplié par une constante.Polynômes en plusieurs indéterminées
Article détaillé : Polynôme en plusieurs indéterminées.Si A est un anneau factoriel, A[X] est factoriel, puis A[X][Y] = A[X,Y] est aussi factoriel et il en est de même de
![A[X_1,X_2,\cdots,X_n]](/pictures/frwiki/50/2c13583dcf37666b288dd8a8f9b13cbf.png) . Un polynôme à n indéterminées sur un anneau factoriel est donc toujours décomposable de manière unique (à un inversible près) en produits de polynômes irréductibles.
. Un polynôme à n indéterminées sur un anneau factoriel est donc toujours décomposable de manière unique (à un inversible près) en produits de polynômes irréductibles.Algorithmes de décomposition
Suivant la nature de l'anneau des coefficients considéré, les algorithmes de factorisation des polynômes en produits d'irréductibles sont de difficulté variable.
Dans le cas de coefficients réels ou complexes, l'obtention d'une factorisation exacte avec des coefficients en écriture décimale est en général impossible, puisque l'écriture d'une racine requiert une infinité de décimales. Cependant de nombreux algorithmes, dont le plus célèbre est la méthode de Newton, permettent d'obtenir des approximations aussi bonnes que souhaitées. Un tel algorithme itératif, sous de bonnes conditions de départ, peut doubler (voire mieux) le nombre de décimales obtenues à chaque itération. Des conditions de départ acceptables peuvent être obtenues en utilisant au préalable des algorithmes de séparation des racines. Le cas des racines multiples, ou extrêmement rapprochées, nécessite des considérations particulières.
Dans le cas des polynômes à coefficients dans les corps finis, pour un polynôme fixé, il n'existe qu'un nombre fini de diviseurs potentiels, les polynômes de degré inférieur. Un algorithme naïf consiste donc à factoriser un polynôme en testant sa divisibilité par les polynômes de degré inférieur, de manière analogue à l'algorithme naïf de division des entiers. Toutefois, des algorithmes bien plus efficaces existent. Ils ont été découverts entre la fin des années 1960 et le début des années 1980, et sont de complexité polynomiale, déterministe ou probabiliste, par exemple l'algorithme de Berlekamp, ou celui de Cantor-Zassenhaus.
De la factorisation des polynômes à coefficients dans les corps finis se déduisent des algorithmes de factorisation dans d'autres domaines. D'abord pour les polynômes dont les coefficients sont des nombres p-adiques, avec la restriction, comme dans le cas des coefficients réels et complexes, qu'on ne peut obtenir en temps fini qu'un nombre fini de terme d'un développement p-adique (les facteurs irréductibles peuvent être de tout degré, et pas seulement de degré 1 ou 2 comme dans les cas réels et complexes). Ceci peut se faire grâce à une version algorithmique du lemme de Hensel. Ensuite, pour les polynômes à coefficients rationnels, ou dans des corps de nombres. Le passage d'une factorisation dans le domaine des coefficients p-adiques à une factorisation à coefficients rationnels est possible car la deuxième s'obtient en regroupant convenablement les facteurs de la première. Il est possible soit de tester toutes ces combinaisons, ce qui peut être de complexité algorithmique exponentielle, soit de ramener ce problème à un problème algorithmique d'algèbre linéaire de type sac à dos. Ces algorithmes progressent encore au début des années 2000 (voir algorithme de van Hoeij).
Enfin, parvenir à la factorisation des polynômes à coefficients entiers est équivalent algorithmiquement à parvenir conjointement à factoriser les entiers et les polynômes à coefficients rationnels.
Voir aussi
- Mathématiques
- Théorème de d'Alembert-Gauss
- Équation polynomiale
- Équation du second degré
- Algorithme de van Hoeij
Catégorie : Polynôme
Wikimedia Foundation. 2010.

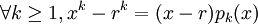
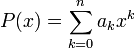
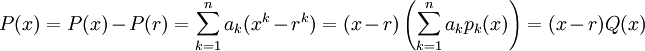
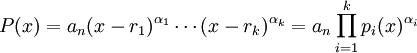
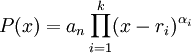
![b=\sqrt[n]a](/pictures/frwiki/51/32e0633d526a3d0c6c72adf7ce42d654.png)