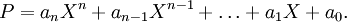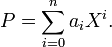- Critere d'Eisenstein
-
Critère d'Eisenstein
En mathématiques, le critère d'Eisenstein donne des conditions suffisantes pour qu'un polynôme à coefficients entiers soit irréductible sur le corps des nombres rationnels (ce qui est une étape pour prouver son irréductibilité sur l'anneau des entiers, la condition supplémentaire étant -- d'après le lemme de Gauss -- que ce polynôme soit primitif, c'est-à-dire que ses coefficients soient premiers entre eux dans leur ensemble).
Enoncé
Considérons un polynôme primitif P à coefficients entiers, que l'on note
Supposons qu'il existe un nombre premier p tel que
-
divise ai- p ne divise pas an,
- p2 ne divise pas a0.
Alors P est irréductible dans
![\mathbb{Z}[X]](/pictures/frwiki/56/8948f9796109cbb4f99d4dd5ba0b3b82.png)
, l'ensemble des polynômes à coefficients entiers. Par suite, P est irréductible dans ![\mathbb{Q}[X]](/pictures/frwiki/49/12e7b267ca89f819cb51e1e108ba6678.png)
, l'ensemble des polynômes à coefficients rationnels.Remarque : si P n'est pas supposé primitif alors il reste irréductible dans
, mais pas nécessairement dans .DémonstrationOn réduit les coefficients de P modulo p. On obtient un polynôme de
![\mathbb{F}_p[X]](/pictures/frwiki/56/840547c82637d4448839097a10351557.png)
de la forme cXn avec 
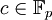non nul.Par l'absurde, si P se factorise en P = QR, où Q et R sont des polynômes de
de degré non nul, en passant modulo p, alors nécessairement on obtient une factorisation de cXn sous la forme de monômes dXk et eXn − k, où de = c.Remarquons maintenant que a0 = Q(0)R(0). D'après la forme de Q et R, on sait que Q(0) et R(0) sont divisibles par p, donc Q(0)R(0) est divisible par p2, et par suite a0 est divisible par p2, ce qui est une contradiction. Donc P est irréductible.
Exemples
Considérons le polynôme P = 3X4 + 15X2 + 10.
Nous examinons différents cas pour les valeurs de p suivantes
- p = 2. 2 ne divise pas 15, on ne peut pas conclure
- p = 3. 3 ne divise pas 10, on ne peut pas conclure
- p = 5. 5 divise 15, le coefficient de X2, et 10 le coefficient constant. 5 ne divise pas 3, le coefficient dominant. En outre, 25 = 52 ne divise pas 10. Ainsi, nous concluons grâce au critère d'Eisenstein que P est irréductible.
Dans certains cas le choix du nombre premier peut ne pas être évident, mais peut être facilité par un changement de variable de la forme Y = X + a, appelé translation.
Par exemple considérons H = X2 + X + 2. L'application du critère semble compromise puisque qu'aucun nombre premier ne divisera 1, le coefficient de X. Mais si nous translatons H en H(X + 3) = X2 + 7X + 14, nous voyons immédiatement que le nombre premier 7 divise le coefficient de X et de le coefficient constant et que 49 ne divise pas 14. Ainsi en translatant le polynôme nous l'avons fait satisfaire le critère d'Eisenstein.
Un autre cas connu est celui du polynôme cyclotomique d'indice un entier premier p, c’est-à-dire le polynôme
.
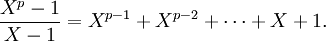Ici, le polynôme satisfait le critère d'Eisenstein, dans une nouvelle variable Y après une translation X = Y + 1. Le coefficient constant est alors égal à p; les autres coefficients sont divisibles par p d'après les propriétés des coefficients binomiaux.
Généralisation
Soit A un anneau intègre et soit P un polynôme à coefficients dans A, noté
On suppose qu'il existe un idéal premier I de A tel que
-
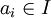pour tout 
,
,
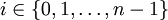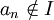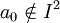, où I2 est le produit de l'idéal I par lui-même.
Alors P est irréductible sur le corps des fractions F(X) de A[X].
Portail des mathématiques
Catégories : Arithmétique modulaire | Anneau | Polynôme
Wikimedia Foundation. 2010.
