Mouvement Central Discret

Mouvement Central Discret: Mouvement central discret

Pour des personnes n'ayant aucun bagage en calcul différentiel et intégral, la mécanique peut quand même se comprendre en utilisant le calcul des différences discrètes : c'est-à-dire transposer les règles différentielles en règles de différence, mais en ajustant la force de manière adroite.

On peut ainsi faire comprendre le Mouvement à force centrale, même à des personnes ne possédant pas le calcul différentiel et intégral ( cf Feynman).

Sommaire

1 Mouvement newtonien discret

2 Loi de force newtonienne discrète

3 Méthode d'itération

4 Loi de Hooke

5 Bibliographie

6 Voir aussi

Mouvement newtonien discret

Le mouvement est plan. Le centre de force est le Soleil placé à l'origine O . Les coordonnées de la planète $P\,$ sont appelées $(x , y)\,$ . Le théorème de Pythagore donne 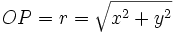$OP = r =\sqrt{x^2 + y^2}\,$ .

On notera les positions successives de la planète $P$ aux temps $t(n) = n \cdot \tau$ , $P(n)\,$ de coordonnées $(x(n),y(n))\,$ .La durée $τ$ est une durée appelée "pas temporel discret du calcul" : plus il est petit et meilleure est la trajectoire, mais plus les calculs sont longs.

On appelle vitesse de la planète selon l'axe 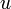$O_x\,$ , $u\,$ et selon l'axe $O_y\,$ , $v\,$ :

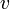Le théorème de Pythagore donne $V =\sqrt{u^2+v^2}\,$ .

Mais attention, on appelle vitesse discrète 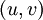$(u , v)\,$ entre le point $P(n)\,$ et le point $P(n+1)\,$ :

$u(n+1)+u(n) = 2\frac{x(n+1)-x(n)}{\tau}\,$ .

et idem pour $O_y\,$ :

$v(n+1)+v(n) = 2\frac{y(n+1)-y(n)}{\tau}\,$ .

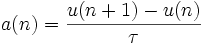L'accélération $(a, b)\,$ sera $a(n) = \frac{u(n+1)-u(n)}{\tau}\,$ et selon $O_y\,$ : $b(n) = \frac{v(n+1)-v(n)}{\tau}\,$ .

Le principe fondamental de la dynamique énoncé par Newton en 1687 consiste à dire : étant deux points initiaux $P(0)\,$ et $P(1)\,$ on donne la règle générale qui à partir de ces deux points permet de calculer le suivant ; alors on continue

On peut en déduire $P(2)\,$

Puis à partir de $P(1)\,$ et $P(2)\,$ , calculer $P(3)\,$

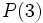
Et continuer ainsi pour calculer tous les points de la trajectoire.

C'est une règle simple. Il en existe de plus sophistiquées, certes.

Loi de force newtonienne discrète

Dans le cas du mouvement des planètes, cas discret, la loi de Newton est légèrement modifiée : la composante de l'accélération selon $O_x\,$ est :

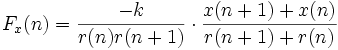
$F_x(n)=\frac{-k}{r(n)r(n+1)}\cdot\frac{x(n+1)+x(n)}{r(n+1)+r(n)}\,$

et idem selon $O_y\,$ :

$F_y(n) =\frac{-k}{r(n)r(n+1)}\cdot\frac{y(n+1)+y(n)}{r(n+1)+r(n)}\,$

Grâce à cette loi de force, on peut démontrer par un calcul dit télescopique (les termes s'éliminent progressivement) que :

l'énergie cinétique s'écrit $T(n) = \frac{1}{2}\cdot m \cdot[u(n)^2+v(n)^2],$

le travail élémentaire de la force s'écrit $w(n)= [x(n+1)-x(n)] \cdot F_x(n)+[y(n+1)-y(n)] \cdot F_y(n)\,$ ,

le travail total $W(n)\,$ est $\sum_{k=0}^{n-1}w(k)\,$ .

On trouve alors la conservation de l'énergie mécanique :

$T(n) + W(n) = T(0) + W(0) = constante\,$ .

En faisant tous les calculs, on trouve $W(n)=\frac{-k}{r(n)}\,$ tout simplement.

Méthode d'itération

Là se pose le vrai problème :

En effet , il faudra résoudre le système de 4 équations (non linéaires) à 4 inconnues x(2),y(2),u(2) et v(2), qui est assez compliqué , mais que tout système type maple est capable de résoudre.

Il suffit alors de réitérer avec x(1),y(1),u(1),v(1) comme point de départ.

On vérifiera qu'au cours du calcul, l'énergie reste bien constante aux arrondis de calculs près. Les trajectoires sont au moins aussi belles que celles données par une méthode de Runge-Kutta d'ordre 4.

Remarque : comme pour tout calcul numérique, on n'opère jamais brutalement avec les valeurs réelles en S.I. qui n'a évidemment aucun sens pour un ordinateur. On opère donc en unité réduite, bâtie à partir du système d'unités naturelles des 4 équations récurrentes à étudier.

Loi de Hooke

Dans ce cas la loi de force est plus simple, puisque l'on remplace la loi de Hooke par la loi de Hooke discrète :

$F_x(n) = - \frac {x(n+1) +x(n)}{r(n+1) +r(n)}$

$F_y(n) = - \frac {y(n+1) +y(n)}{r(n+1) +r(n)}$

Les calculs se conduisent ensuite comme précédemment.

Evidemment cette fois , on obtient une ellipse dont le centre de force O est le centre de l'ellipse.

Note-conjecture : existe-t-il une transformation d'Arnold, de ce problème en le précédent ?

Bibliographie

Greenspan, Computer-oriented mathematical physics, ed Pergamon, ISBN 0080264719

Voir aussi

Analyse numérique des équations différentielles

Dérivée seconde discrète

Laplacien discret

Mouvement à force centrale

Portail de la physique

Ce document provient de « Mouvement central discret ».

Catégories : Article à désacadémiser | Mécanique du point

Contenu soumis à la licence CC-BY-SA. Source : Article Mouvement Central Discret de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Mouvement central discret — Pour des personnes n ayant aucun bagage en calcul différentiel et intégral, la mécanique peut quand même se comprendre en utilisant le calcul des différences discrètes : c est à dire transposer les règles différentielles en règles de… … Wikipédia en Français
Mouvement a force centrale — Mouvement à force centrale En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force … Wikipédia en Français
Mouvement À Force Centrale — En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force. Ce type de mouvement est… … Wikipédia en Français
Mouvement à force centrale — En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force. Ce type de mouvement est… … Wikipédia en Français
Force centrale, mouvement — Mouvement à force centrale En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force … Wikipédia en Français
Mouvement Keplerien — En astronomie, le mouvement keplerien basé sur les 3 lois de Kepler ne donne que peu d indications sur le mouvement des planètes. Cet article se veut un approfondissement complémentaire. Sommaire 1 Quelques éléments de base 1.1 Données… … Wikipédia en Français
Mouvement képlerien — Mouvement keplerien En astronomie, le mouvement keplerien basé sur les 3 lois de Kepler ne donne que peu d indications sur le mouvement des planètes. Cet article se veut un approfondissement complémentaire. Sommaire 1 Quelques éléments de base… … Wikipédia en Français
Mouvement keplerien — En astronomie, le mouvement keplerien basé sur les trois lois de Kepler ne donne que peu d indications sur le mouvement des planètes. Cet article se veut un approfondissement complémentaire. Sommaire 1 Quelques éléments de base … Wikipédia en Français
Constante des aires — Mouvement à force centrale En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force … Wikipédia en Français
Exegese des Principia — Exégèse des Principia Les Principia sont une œuvre tellement indigeste qu il convient de s atteler à en faire la critique : cela ne remet aucunement en question l imagination et la puissance de travail de Newton. Récemment une relecture des… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts