- Espaces de Banach
-
Espace de Banach
Un espace de Banach est un espace vectoriel normé complet pour la distance issue de sa norme. Comme la topologie induite par sa distance est compatible avec sa structure d’espace vectoriel, c’est un espace vectoriel topologique. Les espaces de Banach possèdent de nombreuses propriétés qui font d'eux un outil essentiel pour l'analyse fonctionnelle.
Sommaire
Exemples
Par la suite
 peut être remplacé par
peut être remplacé par  ou
ou  .
.- Les espaces euclidiens
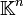 munis de la norme
munis de la norme 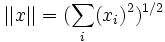 où x = (x1,...,xn) sont des espaces de Banach.
où x = (x1,...,xn) sont des espaces de Banach. - L'espace des fonctions continues définies sur un intervalle :
![f:[a,b] \rightarrow \mathbb{K}](/pictures/frwiki/55/753d3eff0b60766d6e0041a0f7e42bbc.png) muni de la norme
muni de la norme ![||f|| = \sup_{x \in [a,b]}(|f(x)|)](/pictures/frwiki/99/cbd04da41bafb8ac4deb25b0a9fe85ab.png) forme un espace de Banach.
forme un espace de Banach.
Propriété des fermés emboîtés
Soit une suite décroissante de fermés non vides d'un espace de Banach telle que le diamètre de chaque fermé soit réel et que la suite des diamètres tende vers 0. Alors l'intersection des fermés est réduite à un singleton.
Cette propriété permet de démontrer qu'un espace de Banach est de Baire.
Cette propriété peut être fausse sans l'hypothèse que les diamètres tendent vers 0, même si on suppose les fermés bornés.
Théorème de Banach-Steinhaus
Voir l'article de fond : Théorème de Banach-Steinhaus.
Soient E un espace de Banach, et F un espace vectoriel normé. Soit
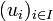 une famille d'éléments de
une famille d'éléments de 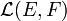 (voir application linéaire) et soit A l'ensemble des vecteurs
(voir application linéaire) et soit A l'ensemble des vecteurs 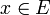 tels que
tels que 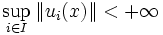 . Alors soit A est maigre, c'est-à-dire réunion dénombrable d'ensembles rares (un ensemble est rare si l'intérieur de son adhérence est vide) et son complémentaire est dense, soit
. Alors soit A est maigre, c'est-à-dire réunion dénombrable d'ensembles rares (un ensemble est rare si l'intérieur de son adhérence est vide) et son complémentaire est dense, soit 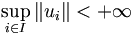 . En particulier, si A = E, seule la seconde éventualité est possible.
. En particulier, si A = E, seule la seconde éventualité est possible.Remarque : la dernière norme utilisée est la norme d'opérateur (ou norme subordonnée).
Littérature
- Stefan Banach : Théorie des opérations linéaires. -- Warszawa 1932. (Monografie Matematyczne; 1) Zbl 0005.20901
Liens internes
Structures topologiques :
Théorèmes d'analyse :
- Théorème de Baire-Banach
- Théorème de Banach-Schauder
- Théorème de Banach-Steinhaus
- Théorème de Hahn-Banach
Biographie :
- Portail des mathématiques
Catégories : Espace de Banach | Espace vectoriel normé - Les espaces euclidiens
Wikimedia Foundation. 2010.
