Theoreme des fermes emboites
- Theoreme des fermes emboites
-
Théorème des fermés emboités
Soit (E,d) un espace métrique que l'on suppose complet. Soit Fn une suite décroissante de fermés non vide de E dont le diamètre tend vers zéro. Le théorème des fermés emboités affirme alors que l'intersection des Fn est réduite à un point.
Démonstration
Si on prend un élément xn dans chaque Fn, la suite (xn) est de Cauchy. En effet, pour un 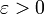 fixé, il existe un rang N à partir duquel on a
fixé, il existe un rang N à partir duquel on a 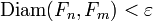 , et en particulier
, et en particulier 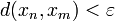 . Cette suite est donc convergente car E est complet. Par ailleurs sa limite x appartient à chaque Fn car si
. Cette suite est donc convergente car E est complet. Par ailleurs sa limite x appartient à chaque Fn car si 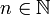 et m>n, alors
et m>n, alors 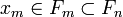 donc
donc 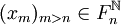 . Fn étant fermé,
. Fn étant fermé,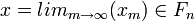 , et ce pour tout n. On a donc prouvé que l'intersection des Fn est non vide.
, et ce pour tout n. On a donc prouvé que l'intersection des Fn est non vide.
Elle est de plus réduite à un point, car s'il existe deux points x et y dans cette intersection, alors comme le diamètre tend vers zéro on a d(x,y) qui tend vers zéro également, donc nécessairement x = y.
Lorsque 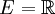 et les fermés sont des intervalles fermés, le théorème prend donc la forme suivante : soit [an,bn] une suite décroissante de segments de
et les fermés sont des intervalles fermés, le théorème prend donc la forme suivante : soit [an,bn] une suite décroissante de segments de  tels que bn − an tende vers zéro, alors l'intersection des segments [an,bn] est un singleton. Ce corollaire particulier est connu sous le nom de théorème des segments emboités.
tels que bn − an tende vers zéro, alors l'intersection des segments [an,bn] est un singleton. Ce corollaire particulier est connu sous le nom de théorème des segments emboités.
 Portail des mathématiques
Portail des mathématiques
Catégories : Espace métrique | Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme des fermes emboites de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème des fermés emboités — En mathématiques, plus précisément en topologie, le théorème des fermés emboîtés affirme que si un espace métrique (E,d) est complet alors, pour toute suite décroissante de fermés non vides Fn de E dont le diamètre tend vers zéro, l intersection… … Wikipédia en Français
Théorème des segments emboîtés — Théorème des fermés emboités Soit (E,d) un espace métrique que l on suppose complet. Soit Fn une suite décroissante de fermés non vide de E dont le diamètre tend vers zéro. Le théorème des fermés emboités affirme alors que l intersection des Fn… … Wikipédia en Français
Theoreme des compacts emboites — Théorème des compacts emboités Soit (E,d) un espace métrique compact. Si (Fn) est une suite décroissante de fermés non vides de E, alors l intersection de tous les Fn est non vide. Autrement dit si (Fn) est une suite décroissante de fermés de E,… … Wikipédia en Français
Théorème des compacts emboités — Soit (E,d) un espace métrique compact. Si (Fn) est une suite décroissante de fermés non vides de E, alors l intersection de tous les Fn est non vide. Autrement dit si (Fn) est une suite décroissante de fermés de E, d intersection vide, alors il… … Wikipédia en Français
Corps des réels — Nombre réel Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs… … Wikipédia en Français
Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… … Wikipédia en Français
Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
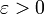 fixé, il existe un rang N à partir duquel on a
fixé, il existe un rang N à partir duquel on a 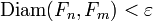 , et en particulier
, et en particulier 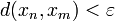 . Cette suite est donc convergente car E est complet. Par ailleurs sa limite x appartient à chaque Fn car si
. Cette suite est donc convergente car E est complet. Par ailleurs sa limite x appartient à chaque Fn car si 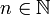 et m>n, alors
et m>n, alors 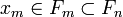 donc
donc 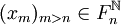 . Fn étant fermé,
. Fn étant fermé,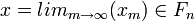 , et ce pour tout n. On a donc prouvé que l'intersection des Fn est non vide.
, et ce pour tout n. On a donc prouvé que l'intersection des Fn est non vide.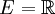 et les fermés sont des intervalles fermés, le théorème prend donc la forme suivante : soit [an,bn] une suite décroissante de segments de
et les fermés sont des intervalles fermés, le théorème prend donc la forme suivante : soit [an,bn] une suite décroissante de segments de  tels que bn − an tende vers zéro, alors l'intersection des segments [an,bn] est un singleton. Ce corollaire particulier est connu sous le nom de théorème des segments emboités.
tels que bn − an tende vers zéro, alors l'intersection des segments [an,bn] est un singleton. Ce corollaire particulier est connu sous le nom de théorème des segments emboités.