- Banach
-
Stefan Banach
Buste de Stefan Banach à Cracovie
Stefan Banach (1892 - 1945) est un mathématicien polonais. Il a donné son nom aux espaces de Banach.
Sommaire
Biographie
Stefan Banach est né le 30 mars 1892 à Ostrowsko près de Cracovie alors territoire de l'Empire Autrichien. Son père s'appelait Stefan Greczek et était l'époux de Katarzyna Banach. Il fait ses études primaires et secondaires à Cracovie, puis est allé poursuivre ses études universitaires à Lviv en Pologne (Ukraine actuelle) de 1910 à 1914. Pendant la guerre, il est réformé, travaille à la construction de routes et suit à l'Université de Cracovie les leçons de mathématiques. En 1916, traversant un parc de Cracovie, Hugo Dyonizy Steinhaus entend prononcer les mots mesure de Lebesgue; c'est ainsi qu'il fit la connaissance de deux jeunes mathématiciens Otto Nikodym et Stefan Banach. Ce fut le début d'une fructueuse collaboration.
En 1919, à l'initiative de Steinhaus, est créée la Société de Mathématiques de Cracovie, transformée en 1920 en Société de Mathématiques de Pologne. Banach y fait de nombreuses communications. En 1920, il devient assistant de Lomnicki à l'Université Technique de Lviv et en 1922 passe son habilitation. Il est nommé professeur en 1924.
En 1929, avec Steinhaus, il crée la revue Studia Mathematica consacrée à l'analyse fonctionnelle. En 1931 commence une série de publications sous le titre de Mathematical Monographs; la direction est assurée par Banach et Steinhaus à Lviv ainsi que par Kuratowski, Mazurkiewicz, et Sierpinski à Varsovie.
En 1939, il est nommé président de la Société de Mathématiques de Pologne.
La Seconde Guerre mondiale fut une période de difficultés avec les occupations soviétique puis nazie. Il put cependant rencontrer Sergueï Sobolev et Pavel Aleksandrov en 1940. Malade, Banach meurt en 1945 à Lviv.
Travaux
Il est un des fondateurs de l'analyse fonctionnelle. La théorie généralise les contributions de Volterra, Fredholm et Hilbert sur les équations intégrales.
Pour résoudre ces problèmes, il a approfondi la théorie des espaces vectoriels topologiques. Dans sa thèse en 1920, il donne la définition des espaces de type (B) que nous appelons aujourd'hui espaces de Banach (les mathématiciens ayant accepté le nom proposé par Frechet).
Plusieurs de ses théorèmes portent son nom, tels
- le théorème de Hahn-Banach (1927) sur l'extension d'une forme linéaire continue définie sur un sous-espace d'un espace vectoriel à l'espace tout entier;
- le théorème Banach-Steinhaus (1927) sur les familles d'applications linéaires continues bornées, conséquence très importante de la propriété de Baire;
- le théorème Banach-Alaoglu, traitant de compacité;
- le théorème de Banach-Schauder (ou encore théorème de l'application ouverte).
Banach a étudié les algèbres dites aujourd'hui de Banach.
Son livre Théorie des opérations linéaires (Teoria operacji liniowych, 1932) expose une synthèse de son travail.
Ses autres travaux touchent à la théorie de la mesure de l'intégration, de la théorie des ensembles et des séries orthogonales.
Il est à l'origine, avec Alfred Tarski, du Paradoxe de Banach-Tarski qui par la simplicité apparente de son énoncé et l'étrangeté de sa conclusion, souligne les difficultés de compréhension qui se cachent dans la notion de parties non-mesurables de
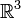. Ces difficultés sont aussi intimement attachées à l'axiome du choix, outil de base de la démonstration.Voir aussi
Articles connexes
- Espace de Banach
- Espace de Hilbert
- Algèbre de Banach
- Théorème de Banach-Steinhaus
- Théorème de Hahn-Banach
- Théorème de Banach-Schauder
- Théorème de Banach-Alaoğlu
- Théorème de Baire-Banach
- Théorème du point fixe de Banach
Liens externes
- Théorie des opérations linéaires Traduction de 1932 (en français)
- (en) John J. O'Connor et Edmund F. Robertson, Stefan Banach, MacTutor History of Mathematics archive.
Portail des mathématiques
Portail de la Pologne
Catégories : Naissance en Petite-Pologne | Mathématicien polonais | Naissance en 1892 | Décès en 1945
Wikimedia Foundation. 2010.
