Espace De Cantor
- Espace De Cantor
-
Espace de Cantor
On appelle espace de Cantor l'espace produit 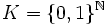 . C'est un espace compact métrisable à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des propriétés équivalentes), totalement discontinu (on dit aussi de dimension 0), qui a la propriété universelle suivante :
. C'est un espace compact métrisable à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des propriétés équivalentes), totalement discontinu (on dit aussi de dimension 0), qui a la propriété universelle suivante :
- Tout espace métrisable à base dénombrable totalement discontinu est homéomorphe à un sous-espace de K.
Cela fournit en particulier un moyen commode pour compactifier les espaces métrisables à base dénombrable totalement discontinus. On en déduit que tout espace mesurable dénombrablement engendré et séparé est isomorphe à une partie de K munie de la tribu induite par la tribu borélienne de K.
L'espace de Cantor est homéomorphe à l'ensemble de Cantor, mais il est équipé naturellement d'une distance ultramétrique analogue à celle sur NN dont on trouvera une description dans l'article « boule ». C'est aussi, en probabilité, l'espace canonique sur lequel on construit le jeu de pile ou face.
L'espace de Cantor K a la puissance du continu, et on démontre par exemple que les boréliens d'un espace métrisable compact ont la puissance du continu dès qu'ils sont non-dénombrables en prouvant qu'ils contiennent un sous-espace homéomorphe à K.
 Portail des mathématiques
Portail des mathématiques
Catégories : Espace topologique remarquable | Georg Cantor
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Espace De Cantor de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Espace de cantor — On appelle espace de Cantor l espace produit . C est un espace compact métrisable à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des propriétés équivalentes), totalement discontinu (on dit… … Wikipédia en Français
Espace de Cantor — En mathématiques, plus précisément en topologie, on appelle espace de Cantor l espace produit . Propriétés C est un espace compact métrisable à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des … Wikipédia en Français
Espace a base denombrable — Espace à base dénombrable Un espace topologique est dit à base dénombrable si sa topologie admet une base dénombrable. Tout sous espace d un espace à base dénombrable et tout produit dénombrable d espaces à base dénombrable sont eux mêmes à base… … Wikipédia en Français
Espace À Base Dénombrable — Un espace topologique est dit à base dénombrable si sa topologie admet une base dénombrable. Tout sous espace d un espace à base dénombrable et tout produit dénombrable d espaces à base dénombrable sont eux mêmes à base dénombrable ; d autre … Wikipédia en Français
Espace totalement discontinu — En mathématiques, plus précisément en topologie, un espace totalement discontinu est un espace topologique qui est « le moins connexe possible » au sens où il n a pas de partie connexe non triviale. Dans tout espace topologique, l… … Wikipédia en Français
Cantor — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Pour l’article homophone, voir Kantor (homonymie). Sur les autres projets Wikimedia : « Cant … Wikipédia en Français
Espace à base dénombrable — Ne doit pas être confondu avec Espace à base dénombrable de voisinages (en). En mathématiques, plus précisément en topologie, un espace est dit à base dénombrable si sa topologie admet une base dénombrable. La pl … Wikipédia en Français
CANTOR (G.) — Source de nombreux paradoxes depuis l’Antiquité, l’infini a toujours été un sujet de préoccupation et d’inquiétude pour les mathématiciens qui cherchaient à l’appréhender. La nécessité d’asseoir le calcul infinitésimal sur des bases solides avait … Encyclopédie Universelle
Espace Localement Compact — En topologie, un espace localement compact est un espace qui, sans être nécessairement compact lui même, admet des voisinages compacts pour tous ses points. On peut y généraliser (au moins partiellement) beaucoup de résultats sur les espaces… … Wikipédia en Français
Espace Topologique — La topologie générale est une branche des mathématiques qui fournit un vocabulaire et un contexte général pour traiter des notions de limite, de continuité, dans le cadre d un continuum ou d un espace discret, voire fini. Dans ce contexte, les… … Wikipédia en Français
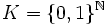 . C'est un espace compact métrisable à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des propriétés équivalentes), totalement discontinu (on dit aussi de dimension 0), qui a la propriété universelle suivante :
. C'est un espace compact métrisable à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des propriétés équivalentes), totalement discontinu (on dit aussi de dimension 0), qui a la propriété universelle suivante :