Error correction code

Un code correcteur est une technique de codage basée sur la redondance. Elle est destinée à corriger les erreurs de transmission d'une information (plus souvent appelée message) sur une voie de communication peu fiable.

La théorie des codes correcteurs ne se limite pas qu'aux communications classiques (radio, câble coaxial, fibre optique, etc.) mais également aux supports pour le stockage comme les disques compacts, la mémoire RAM et d'autres applications où l'intégrité des données est importante.

Sommaire 1 Problématique 1.1 Description intuitive 1.2 Classification de la problématique 1.3 Redondance et fiabilité 1.4 Structures mathématiques 2 Formalisation du problème 2.1 Alphabet 2.2 Code en bloc 2.3 Encodage 3 Exemples de code en blocs 3.1 Code de répétition 3.2 Somme de contrôle 4 Redondance et fiabilité 4.1 Distance de Hamming 4.2 Code parfait 5 Théorie algébrique des codes en blocs 5.1 Codes linéaires 5.1.1 Matrice génératrice 5.1.2 Matrice de contrôle 5.1.3 Syndrome et décodage 5.2 Codes cycliques 5.3 Autres codes 6 Quelques codes correcteurs 7 Quelques applications typiques 8 Différences entre un code correcteur et un code d'authentification 9 Voir aussi 9.1 Bibliographie 9.2 Liens externes

Problématique

Description intuitive

Les codes correcteurs d'erreurs ont leur source dans un problème très concret lié à la transmission de données. Dans la grande majorité des cas, une transmission de données se fait en utilisant une voie de communication, le canal de communication, qui n'est pas entièrement fiable. Autrement dit, les données, lorsqu'elles circulent sur cette voie, sont susceptible d'être altérées.

Par exemple lors d'une communication radio, la présence de parasites sur la ligne va perturber le son de la voix. Il y a alors essentiellement deux approches possibles :

• augmenter la puissance de l'émission
• ajouter de la redondance à l'information

Si l'on reprend l'exemple de la communication radio, augmenter la puissance de l'émission signifie crier ou avoir un meilleur émetteur. Cette technique a bien évidemment ses limites, et aura du mal à être utilisée dans des sondes spatiales, sans même prendre en considération des contraintes sur les ressources en énergie.

L'autre solution va consister à ajouter des données, ce qui donne lieu au code des aviateurs qui diront «Alpha Tango Charlie» dans le seul but de transmettre correctemment «ATC» à travers leur radio. La séquence «Alpha Tango Charlie», même déformée par la friture, sera bien plus reconnaissable pour l'oreille humaine qu'un «ATC» déformé.

Classification de la problématique

Les problématiques apportées par l'industrie sont diverses. Dans le cas de la transmission de données, par exemple sur internet, le rôle du code correcteur se limite parfois à la détection des erreurs. C'est le cas pour le protocole TCP. La correction est alors réalisée par une nouvelle demande de transmission du message.

Pour d'autres situations, l'objectif est la correction d'erreurs, sans nouvelle demande de transmission. Là encore, plusieurs configurations se présentent. La communication sur ordinateur par le port série utilise un code dont l'objectif est la correction de petites erreurs relativement fréquentes mais isolées. Dans le cas du disque compact, les erreurs sont aussi causées par des rayures ou des impuretés du support, elles sont moins fréquentes mais beaucoup plus volumineuses. La norme de la société Philips impose la capacité de correction d'erreurs dans le cas d'une rayure de 0,2 millimètre, dans la pratique, le code utilisé corrige jusqu'à 4096 bits consécutifs soit une rayure de plus d'un millimètre de large.

Le disque compact présente une nouvelle situation, celle de l' effacement. Dans ce contexte, et à la différence du paragraphe précédent, le message transmis possède l'indication de la détérioration. La détection des erreurs n'est plus nécessaire, toute l'information se concentre sur la reconstitution du message détérioré.

Cette variété de situations explique la multiplicité des techniques utilisées pour les codes correcteurs. On peut citer les sommes de contrôle pour la simple détection, le code BCH pour les ports série ou encore une variante du code de Reed-Solomon pour les disques compacts. Beaucoup de solutions industrielles sont hybrides, comme par exemple le code de Hamming ou encore celui utilisé pour le Minitel.

D'autres contraintes industrielles se greffent sur la problématique des codes correcteurs. Le coût d'implémentation en est un exemple. Pour une solution grand public, la technique d'encodage et de décodage doit être peu onéreuse. La vitesse de reconstitution des messages est aussi un facteur pris en compte.

Redondance et fiabilité

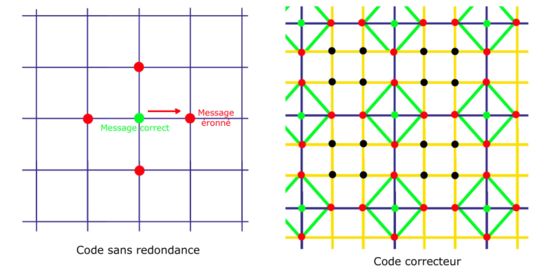
Tous les codes correcteurs subissent une contrainte du même ordre. Si le message contient une information altérée, une information supplémentaire est nécessaire pour, soit détecter l'erreur, soit la corriger. La formalisation est la suivante. Le message transmis, appelé code est plongé dans un espace plus vaste, comme illustré dans la figure de droite.

Le cas d'un code sans redondance est illustré à gauche. Si un message en vert subit, lors de sa transmission, une altération, alors un nouveau message en rouge est transmis. Aucune information ne laisse supposer qu'une erreur a été commise. Pour pallier cet état, l'objectif est d'entourer les messages licites, correspondant aux intersections des quadrillages sur les figures, par des messages connus pour contenir des erreurs, et de réaliser la transmission après. Ces redondances sont illustrées sur la figure de droite par les intersections du quadrillage orange. Si une unique erreur se produit, alors le message transmis correspond à un point rouge. Si la redondance a été habilement construite, alors il n'existe qu'un point licite en vert proche du point rouge reçu.

Un code correcteur propose une géométrie où les messages licites sont le plus possible éloignés les uns des autres. Les boules centrées sur les bons codes, si elles ne s'intersectent pas, permettent de retrouver le bon message, correspondant à son centre. Une perturbation, tant qu'elle reste suffisamment petite pour ne pas faire sortir le code de sa boule est corrigible.

Les points noirs ne sont d'aucune utilité. Il est nécessaire de parcourir deux segments du quadrillage pour relier un point noir d'un point licite. Le code correcteur illustré engendre alors une ambiguïté. En effet, tous les points rouges sont à une distance de deux segments de deux points verts, une double erreur n'est donc généralement pas corrigible. Les points noirs ne servent à rien et ils prennent de la place. Ils présentent une redondance inutile.

Structures mathématiques

Créer une bonne géométrie optimale rapide et peu chère demande de structurer l'espace des codes. Ces structures sont essentiellement réalisées avec des outils mathématiques. L'utilisation des corps finis est presque universelle. L'un est particulièrement utilisé, celui noté F₂ correspondant au corps à deux éléments 0 et 1. La théorie des corps finis démarre par les travaux de Frobenius (1849 - 1917). Il utilise la théorie de Galois pour expliciter leur comportement. Ses travaux sont la base de nombreux développements de la théorie des codes correcteurs. Ces corps sont particulièrement adaptés.

• Ils correspondent à des structures discrètes par opposé à continu. En conséquence ils sont plus simples à modéliser par l'électronique et l'informatique.

• Ils forment la base de nombreux développements. La théorie des espaces vectoriels permet la création de géométrie utile. L'algèbre linéaire est adapté à la mesure du volume des redondances inutiles, ils servent de support à toute une famille de codes correcteurs: les codes linéaires. L'anneau des polynômes à coefficients dans un corps fini est riche en propriétés. Il permet de généraliser la notion de preuve par neuf avec des améliorations notoires (cf l'article Somme de contrôle). Dans ce cas, si la détection d'altérations est possible, la correction automatique ne l'est pas. Les polynômes possèdent des propriétés analogues, et la localisation des erreurs devient possible. De plus, la multiplication est particulièrement aisée. Elle correspond à celle des entiers avec en moins le problème de la retenue. Or, en informatique, la retenue représente l'essentiel du temps de calcul. Beaucoup de codes correcteurs se fondent sur les propriétés des polynômes, ils sont regroupés sous le nom de code cyclique. Enfin, l'arithmétique moderne utilise largement les corps finis, à travers des outils comme les fonctions elliptiques. S'ils demandent un niveau d'abstraction élevé, ils permettent d'obtenir des résultats difficiles. Elles sont utilisées pour certains codes correcteurs, comme celui de Goppa, leur importance industrielle est néanmoins pour l'instant encore faible.

Formalisation du problème

Alphabet

Afin de préciser les questions que se pose la théorie des codes, et les problèmes qu'elle rencontre, l'article considère le cas d'un canal discret. L'information à transmettre peut être vue comme une suite x de symboles pris dans un ensemble fini (il s'agit le plus souvent de bits, donc de 0 et de 1).

• Un alphabet est un ensemble fini non vide, ses éléments sont appelés lettres ou symboles.
• Un message ou un mot est une suite à valeur dans un alphabet, il correspond à une suite de lettres.

L'objectif d'un code correcteur est la transmission fiable d'un message. Dans cet article les alphabets sont notés A ou A', le cardinal d'un alphabet est noté q, et un message m.

Code en bloc

Dans le cas général, les messages à transmettre n'ont pas de longueur fixe. Cette situation existe, par exemple, pour une communication téléphonique. En revanche, il est plus simple de développer un code correcteur pour des messages d'une longueur fixe.

La solution utilisée consiste à segmenter la difficulté. Dans un premier temps, est traité le cas d'un message de longueur fixe. Pour le cas général, une solution simple consiste à concaténer une suite de blocs. La méthode la plus répandue, car la plus efficace est celle du code convolutif.

• La longueur d'un message désigne le nombre de lettres qu'il contient.
• Un code en bloc est un code correcteur traitant des messages de longueur fixe.

Dans la suite de l'article, la longueur d'un message est noté k. L'ensemble des messages est noté E et son cardinal M. M est un entier inférieur ou égal à q^k.

Encodage

Comme le montre le paragraphe redondance et fiabilité, il n'est pas toujours judicieux de transmettre le message m. L'ajout d'une redondance peut être pertinente. Pour répondre à cet objectif, il existe une fonction φ injective de E dans un ensemble F, la transmission a lieu sur φ(m) et non sur m. L'injectivité est nécessaire, car sinon deux messages distincts ne seraient plus distinguables par le récepteur. F est l'ensemble des suites finies de longueur n un entier strictement positif à valeur dans A' un alphabet. Dans le cas général l'alphabet de F diffère de celui de E.

Avant sa transmission, le message est encodé, c'est-à-dire qu'il est transformé en une autre suite y=φ(x) de symboles. Ensuite, y est transmis par un canal bruité qui va, éventuellement le modifier en y'. Pour terminer, un décodeur essaie de retrouver le message x à partir de y'. Il est théoriquement équivalent de rechercher y, puisque l'encodage est une injection. Lorsque y diffère de y', on parle d'erreur(s) ou d'altération(s).

• L'application φ de E dans F est appelée encodage.
• La longueur n des suites de F est appelée dimension du code ou simplement dimension.
• L'image φ(E), sous-ensemble de F est appelée code.
• Un mot du code est un élément du code.

Exemples de code en blocs

Code de répétition

Un exemple simple est celui du code de répétition. La cas étudié ici est celui d'un code binaire, c’est-à-dire que les deux alphabets A et A' sont confondus et égaux à {0,1}. La longueur du code est égale à un et la dimension à trois.

L'application φ est définie sur les deux valeurs: 0 et 1, par une triple définition du message. De manière formelle, on obtient :

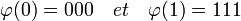
Si une unique altération se produit, alors un système de vote permet de retrouver le message d'origine. Ce code correcteur possède l'avantage de non seulement détecter une erreur, mais aussi de permettre une correction automatique. En revanche, il est cher, c’est-à-dire que sa dimension est élevée par rapport à la longueur des mots transmis.

Somme de contrôle

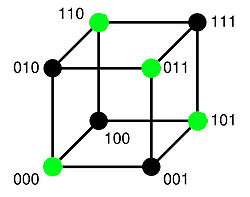
Messages = E	Codes = φ(E)
00	000
01	101
10	110
11	011

L'objectif n'est plus ici la correction automatique mais la détection d'une unique erreur. Les deux alphabets sont binaires, les messages sont de longueur deux et le code de dimension trois.

L'encodage consiste à ajouter un bit de parité, qui vaut zéro si la somme des lettres est paire et un sinon. La table de correspondance de l'encodage est donnée à droite.

La figure de gauche est une illustration géométrique du code. Elle représente l'ensemble d'arrivée F. Les mots du code sont en vert. Une unique erreur correspond à un déplacement sur le cube le long d'une arête. Dans ce cas, le récepteur reçoit un point noir dont la somme de toutes les lettres est un entier impair. Il est donc possible de déterminer l'existence d'une erreur.

En revanche, un point noir est toujours à proximité de trois points verts, le récepteur ne dispose donc d'aucun moyen pour une correction automatique.

Cette technique est généralisable à d'autres alphabets et pour des codes de longueurs quelconques. Elle est économique, c'est la raison pour laquelle elle est largement utilisée. En revanche, et à la différence de l'exemple précédent, la correction impose une nouvelle transmission.

Redondance et fiabilité

Distance de Hamming

Le concept le plus utilisé pour la modélisation de la redondance est celui de la distance de Hamming. À deux mots du code, elle associe le nombre de lettres qui diffèrent.

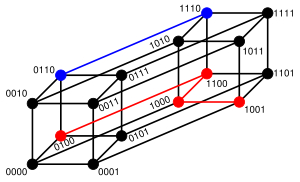
La distance de Hamming entre "ramer" et "cases" est 3.

La figure de droite illustre le cas où les lettres de l'alphabet sont binaires et la dimension du code égale à quatre. La distance entre 0110 et 1110 est égale à un car il est nécessaire de parcourir un segment du graphique pour joindre les deux mots. On peut aussi remarquer que les deux mots diffèrent seulement par leur première lettre. La même approche montre que la distance entre 0100 et 1001 est égale à trois.

Ce concept permet la définition suivante :

• La distance minimale d'un code correcteur est la plus petite distance au sens de Hamming entre deux mots du code.

Cette définition permet de formaliser les trois paramètres les plus important d'un code en blocs.

• Les paramètres d'un code en blocs sont la longueur du code n, le nombre M de mots du code et la distance minimale δ. Ils sont en général noté {n, M, δ}

Code parfait

Usuellement, on considère que le mot de code émis est celui se trouvant le plus près du mot reçu, ce qui revient à supposer que le minimum de lettres a été modifié. Ce procédé conduit à une erreur de décodage chaque fois que l'erreur est supérieure à la capacité corrective du code. La question naturelle est celle de la valeur de t correspondant au nombre maximum d'erreurs corrigibles.

Une interprétation géométrique donne un élément de réponse. les boules fermées de rayon t centrées sur les mots de code doivent être disjointes. La capacité de correction d'un code correspond au plus grand entier t vérifiant cette propriété, c'est aussi le plus grand entier strictement plus petit que δ/2. Elle permet de définir une première majoration, appelée borne de Hamming :

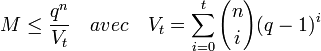
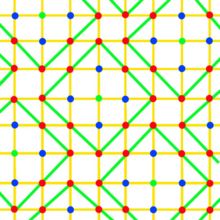
La figure de gauche correspond à une configuration idéale, correspondant au cas où les boules fermées de rayon t et de centre les mots du code forment une partition de l'espace F. Les points du code, en vert, sont espacés d'une distance de cinq entre eux. Si la transmission ne produit jamais plus de deux altérations, alors les erreurs sont toutes corrigibles. Les points à une distance de un d'un mot de code sont en bleu, ceux à une distance de deux en rouge et la frontière des boules est indiquée en vert. Il n'existe aucune redondance inutile, le code est le plus compact possible pour garantir la correction certaine de t erreurs. Pour de tels codes, la majoration de la borne de Hamming est une égalité. Ils sont dit parfaits. L'exemple le plus simple est celui de Hamming binaire de paramètres [7,4,3].

Théorie algébrique des codes en blocs

Si l'analyse qu'apporte la distance de Hamming et les codes parfaits propose un cadre permettant d'évaluer l'efficacité d'un code, elle n'offre pas de solution pratique pour en construire.

La solution consiste à équiper les ensembles E et F de structures algébriques plus riches. Pour cela, les alphabets A et A' sont identifiés et munis d'une structure de corps fini. Le cas le plus fréquent consiste à choisir le corps F₂ ou l'une de ses extensions finies. Ce corps correspond à l'alphabet binaire dont les tables d'addition et de multiplication sont données ci-dessous:

+   0   1   0   0  1  1   1  0

.   0   1   0   0  0  1   0  1

Ce corps, ou ses extensions sont adaptés à un traitement informatique, qui, dans sa grande généralité travaille sur l'alphabet binaire.

Codes linéaires

Si les alphabets sont un même corps finis E et F héritent naturellement d'une structure d'espace vectoriel. Choisir alors l'application d'encodage φ une application linéaire simplifie grandement la problématique.

Les paramètres d'un code linéaire sont notés de manière légèrement différente de ceux des codes quelconques. L'espace E est vectoriel, il est décrit uniquement par sa dimension, correspondant à la longueur du code. Ils sont notés [n,k, δ].

Peu de codes linéaires sont parfaits, et ils sont soit de petites dimensions soit de petite distance minimale. Une autre majoration, plus générale et de même nature que la borne de Hamming existe :

• La majoration suivante est vérifiée pour tous les codes linéaires. Elle se nomme borne de Singleton :

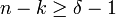
Si la borne est atteinte, on parle alors de code MDS pour maximum distance séparable.

Matrice génératrice

L'encodage est obtenu par l'application d'une matrice, dite matrice génératrice. Elle est toujours équivalente à une forme particulièrement simple, appelée code systématique, les premières coordonnées d'un mot du code correspondent au message, les dernières décrivent la redondance, elles sont appelées sommes de contrôle ou, dans le cas d'un code cyclique contrôles de redondance cyclique.

Matrice de contrôle

La validation du décodage est encore simplifiée. Il existe une application linéaire de F dans un espace de dimension n -k ayant comme noyau exactement le code. Sa matrice est dite de matrice de contrôle. Dans le cas, le plus fréquent dans l'industrie, du code systématique, la matrice de contrôle s'obtient directement à partir de la matrice génératrice et elle possède encore une forme particulièrement simple.

Valider un message reçu revient à vérifier que l'application de la matrice de contrôle à ce message est bien égale au vecteur nul.

Syndrome et décodage

La linéarité du code assure un décodage aisé. Si un message x est reçu, alors la détection d'erreurs est réalisée par la matrice de contrôle H. En effet, des altérations détectables ont eu lieu si et seulement si H.^tx est différent du vecteur nul. Si le nombre d'erreurs présentes dans le message est inférieur à t, le nombre d'altérations assurément détectables, alors H.^tx possède un unique antécédent e dans la boule fermée de centre le vecteur nul et de rayon t. Le message corrigé est x - e. Le vecteur H.^tx est appelé syndrome.

Dans le cas où le nombre d'erreurs est supérieur à t il existe plusieurs antécédents de poids minimal et les altérations ne sont plus assurément corrigibles. La solution idéale consiste à demander une nouvelle transmission.

Si le nombre de syndromes est petit, une table de correspondance entre les syndromes et leurs antécédents de plus petits poids est envisageable. Une telle table est nommé tableau standard et le décodage associé décodage par tableau standard. Si l'espace des syndromes est trop vaste, il est nécessaire de calculer son antécédent à la réception du message altéré.

Codes cycliques

Ces codes sont plus compliqués et reposent sur l'utilisation des propriétés des polynômes dans un corps fini. Le contrôle de redondance cyclique (CRC pour cyclic redundancy check) consiste à considérer un bloc de données comme la représentation des coefficients d'un polynôme que l'on divise ensuite par un polynôme fixe et prédéterminé. Les coefficients issus de cette division constituent le CRC et servent de code correcteur. La vérification des données se fait en multipliant le polynôme fixe par les coefficients du CRC et en comparant le résultat avec les données. On peut également calculer le CRC des données reçues et comparer avec le CRC reçu.

Autres codes

Les structures utilisées dans les codes correcteurs ont tout d'abord été très simples (par exemple celle d'espace vectoriel), puis se sont complexifiés avec une meilleure compréhension des problèmes théoriques. La théorie des codes correcteurs en arrive même à utiliser la géométrie arithmétique pour construire des codes.

Quelques codes correcteurs

Voici différents types de codes correcteurs :

• Codes de Hamming
• Codes de Golay
• Codes de Reed-Müller
• Codes de Goppa
• Codes de Xing
• Codes de Reed-Solomon

Quelques applications typiques

La transmissions d'informations peut-être sujet à des perturbations. Voici quelques applications touchés par ces perturbations :

• les téléphones cellulaires sont mobiles, relativement peu puissants, et souvent utilisés soit loin des antennes relais, soit dans un environnement urbain très bruyant du point de vue électromagnétique;
• les sondes spatiales n'ont pas à leur disposition d'énormes quantités d'énergie pour émettre des messages, se trouvent à des distances astronomiques, et leur antenne, même si elle est orientée le mieux possible, n'est pas parfaite;
• en cas de conflit armé, les communications adverses sont une des cibles privilégiées pour le brouillage et la guerre électronique
• les images disque contiennent pour certains formats (par exemple Mode 2 Form 1) des codes EDC et ECC pour contrôler les données gravées, et cela par secteur.

Différences entre un code correcteur et un code d'authentification

Le théorie des codes correcteurs s'intéresse à des perturbations aléatoires ou suivant une distribution particulière. Il n'y a pas d'"intelligence" dans ce bruit dans le sens où il ne s'agit pas d'une tentative frauduleuse de perturbation de ligne mais le résultat d'un phénomène physique inhérent au canal de transmission. Les codes d'authentification sont au contraire utilisés pour contrer un adversaire intelligent qui va tenter de modifier les données selon une procédure particulière qui s'éloigne du bruit sur la ligne. Les buts et les conditions de fonctionnement sont donc différents. Le premier concept est lié à la théorie de l'information alors que le deuxième est du ressort de la cryptologie et ne vise pas à rétablir l'information, tout au plus confirmer que l'information est valide.

Toutefois, dans le cas d'un brouillage volontaire (guerre électronique), les deux notions s'approchent puisque il faut éviter que l'attaquant réduise les capacités de transmission tout en assurant l'authenticité des informations.

Voir aussi

• Graphe de Hamming
• Limite de Shannon
• Turbo code
• Méthode de décodage
• Chipkill

Bibliographie

• M. Demazure - "Cours d'algèbre", chapitres 6 à 13 - (éd Cassini, Paris, 2008) - 320 p. - ISBN 978-2-84225-127-7
• B. Martin - "Codage, cryptologie et applications" - (éd. Presses Polytechniques et Universitaires Romandes (PPUR), 2004) - 354 p. - ISBN 978-2-88074-569-1
• J.-G. Dumas, J.-L. Roch, E. Tannier et S. Varrette - "Théorie des codes (Compression, cryptage, correction)" - (éd Dunod, 2007) - 352 p. - ISBN 978-2-10-050692-7

Liens externes

• (fr) Polycopié du cours dispensé à l'ENSIMAG

• Portail des mathématiques
• Portail de l’informatique
• Portail de la sécurité informatique