Equivalence forte

Une grammaire est un formalisme permettant de définir une syntaxe et donc un langage formel, c'est-à-dire un ensemble de mots admissibles sur un alphabet donné.

La notion de grammaire formelle est particulièrement utilisée en programmation logique, compilation (analyse syntaxique), en théorie de la calculabilité et dans le traitement des langues naturelles (tout particulièrement en ce qui concerne leur morphologie et leur syntaxe).

Langages

Un langage est un ensemble de mots, qui sont simplement des séquences de symboles choisis dans un ensemble (en général fini) appelé alphabet. Formellement, si A est un ensemble, on note A ^* le monoïde libre sur A, c'est-à-dire l'ensemble des suites finies d'éléments de A, muni de l'opération de concaténation de deux mots. Un langage sur l'alphabet A est par définition un sous-ensemble de A ^* .

Souvent, les « symboles » que l'on considère lorsqu'on définit un langage par une grammaire formelle sont constitués de plusieurs caractères, de sorte qu'ils correspondent plutôt à ce que l'on appelle des mots dans la langue courante. De même, les « mots » du langage correspondent plutôt à des phrases ou à des textes. Lorsqu'il y a ambiguïté, on parle de lettres ou de caractères pour les symboles de l'alphabet utilisé pour coder les informations ; et on réserve le mot symbole pour ceux de l'alphabet abstrait, qui sont les éléments de base du langage.

Par exemple :

• A1 = { a, b, c, d, e } est un alphabet contenant 5 symboles, traditionnellement appelés lettres dans ce cas précis ;
• A2 = { 2, 5, @, $, & } est un autre alphabet contenant 5 symboles ;
• A3 = { Dét, Adj, Verbe, Nom, Coord, Prép } est un alphabet de 6 symboles pouvant décrire, par exemple, la structure syntaxique d'une phrase dans une langue naturelle.

Grammaires

Une grammaire formelle (ou, simplement, grammaire) est constituée des quatre objets suivants:

• Un ensemble fini de symboles, appelés symboles terminaux (qui sont les « lettres » du langage), notés conventionnellement par des minuscules,
• Un ensemble fini de symboles, appelés non-terminaux, notés conventionnellement par des majuscules,
• Un élément de l'ensemble des non-terminaux, appelé axiome, noté conventionnellement S,
• Un ensemble de règles de production, qui sont des paires formées d'un non-terminal et d'une suite de terminaux et de non-terminaux ; par exemple, A → ABa.

Appliquer une règle de production consiste à remplacer dans un mot une occurrence du membre de gauche de cette règle par son membre de droite ; l'application successive de règles de productions s'appelle une dérivation. Le langage défini par une grammaire est l'ensemble des mots formés uniquement de symboles terminaux qui peuvent être atteints par dérivation à partir de l'axiome.

Ainsi, la grammaire définie par les terminaux {a, b}, le non-terminal S, l'axiome S et les deux règles de production suivantes :

S → aSb

S → ε (où ε représente le mot vide)

représente le langage des mots de la forme aⁿbⁿ (un certain nombre de a – éventuellement 0, en vertu de la deuxième règle –, suivis du même nombre de b) : {ε, ab, aabb, aaabbb…}.

Hiérarchie de Chomsky

Lorsque le linguiste Noam Chomsky a dégagé la notion de grammaire formelle, il en a proposé une classification appelée de nos jours hiérarchie de Chomsky. Elle est formée des quatre niveaux suivants, du plus restrictif au plus large.

• Les langages de type 3, ou langages rationnels : ce sont les langages définis par une grammaire linéaire à gauche (c'est-à-dire une grammaire dont chaque membre droit de règle commence par un non-terminal), une grammaire linéaire à droite (c'est-à-dire une grammaire dont chaque membre droit de règle finit par un non-terminal) ou une expression rationnelle ; ou bien encore les langages reconnus par un automate fini.
• Les langages de type 2, ou langages algébriques : ce sont les langages définis par une grammaire formelle hors-contexte, ou bien encore les langages reconnaissables par un automate à pile non déterministe. La plupart des langages de programmation, sans être à proprement parler des langages algébriques, en sont assez proches pour que les techniques d'analyse des langages algébriques s'y adaptent.
• Les langages de type 1, ou langages contextuels : ce sont les langages définis par une grammaire contextuelle, ou encore les langages reconnaissables par une machine de Turing non-déterministe à ruban de longueur bornée par un multiple fixé de la longueur du mot d'entrée.
• Les langages de type 0, ou langages récursivement énumérables. Cet ensemble inclut tous les langages définis par une grammaire formelle. C'est aussi l'ensemble des langages acceptables par une machine de Turing (que l'on autorise à boucler sur un mot qui n'est pas du langage).

Outre les quatre types de la hiérarchie de Chomsky, il existe des classes intermédiaires remarquables :

• entre 3 et 2 : les langages hors-contextes déterministes, reconnaissables par automate à pile déterministe ;
• entre 1 et 0 : les langages récursifs, c'est-à-dire reconnaissables par une machine de Turing (celle-ci doit refuser les mots qui ne sont pas du langage).

Les six types ci-dessus sont strictement inclus les uns dans les autres. Si dans le type 1, on transforme « non déterministe » en « déterministe », on obtient un type plus petit, mais on ne sait pas montrer s'il est strictement inclus dans le type 1 ou s'il est égal à celui-ci.

Analyse

Un analyseur pour un langage formel est un programme informatique qui décide si un mot donné en entrée appartient ou non au langage, et éventuellement en construire une dérivation.

On dispose de méthodes systématiques pour écrire des programmes d'analyse des langages de type 2 ou 3 dans la hiérarchie de Chomsky. Les interpréteurs ou compilateurs comprennent presque toujours une phase d'analyse lexicale, qui consiste à reconnaître des langages de type 3, suivie d'une phase d'analyse syntaxique qui est une analyse de langage de type 2. L'analyse lexicale porte sur une suite de caractères et produit une suite de lexèmes, qui servent à leur tour d'éléments de l'alphabet lors de l'analyse syntaxique.

Des outils comme lex et yacc facilitent l'écriture, respectivement, d'analyseurs lexicaux et d'analyseurs syntaxiques, en produisant automatiquement des portions de programmes à partir d'une spécification de ce langage. Les constructeurs d'analyseurs syntaxiques utilisent le plus souvent une variante de la forme de Backus-Naur, qui est une notation pour les grammaires hors-contexte ; tandis que les constructeurs d'analyseurs lexicaux emploient le formalisme moins lourd des expressions rationnelles.

Exemples de grammaires

Expressions arithmétiques

On peut définir des expressions arithmétiques de la façon suivante :

 exp ::= exp + exp
       | exp × exp
       | (exp)
       | num
 num ::= 0num
       | 1num
       | 2num
       | 3num
       | 4num
       | 5num
       | 6num
       | 7num
       | 8num
       | 9num
       | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Les non-terminaux sont ici implicitement exp et num, les terminaux sont +, ×, (, ) et les chiffres. L'axiome est exp.

La dérivation suivante est un exemple d'utilisation de cette grammaire.

 exp → exp × exp → num × exp → 3 × exp → 3 × num → 3 × 1num → 3 × 18

Il convient de remarquer que la définition donnée permet de reconnaître les expression arithmétiques, mais non de les analyser ; En effet, la priorité des opérateurs n'est pas rendue par cette grammaire.

Langage de programmation simple

Définir un langage de programmation simple n'est pas très compliqué. Cette grammaire reconnaît un langage de programmation ressemblant à pascal. Voici un exemple de programme calculant fact(10)

  begin
  int a;
  int b;
  a:=10;
  b:=1;
  while(a>1) do
    b:=a*b;
    a:=a-1;
  od;
  print b;
  end

 program ::= begin listinstr end
 listinstr ::= instr listinstr
             | instr
 instr ::= int id ;
         | id := expr ;
         | print expr ;
         | while ( cond ) do listinstr od ;
 expr ::= expr - expr1
        | expr1
 expr1 ::= expr1 * expr2
         | expr2
 expr2 ::= id
         | num
         | ( expr )
 cond ::= expr condsymb expr
 condsymb ::= > | < | >= | <= | != | =

les terminaux étant id, num, begin, end, int, print, while, (, ), do, od, ;, et les symboles de comparaison. Remarquons qu'avec une telle grammaire (de type 2 dans la hiérarchie de Chomsky) on ne peut pas vérifier que toutes les variables ont été déclarées (pour cela il faut une grammaire de type 1). Il faudrait aussi ajouter des règles pour num (comme plus haut) et pour id.

Logique propositionnelle classique

La syntaxe de la logique propositionnelle classique ou calcul des propositions peut se définir de la façon suivante :

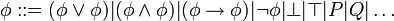
P, Q, ... sont les variables propositionnelles (terminaux).

L-System

Un L-System (ou Système de Lindenmayer) est une grammaire formelle.

Notion d'équivalence

Équivalence forte

Deux grammaires sont dites fortement équivalentes si et seulement si

1. Elles reconnaissent exactement le même langage.
2. Elles utilisent exactement le même arbre syntaxique pour analyser une même phrase.

Équivalence faible

Deux grammaires sont dites faiblement équivalentes si et seulement si

1. Elles reconnaissent exactement le même langage.

Les grammaires fortement équivalentes sont donc toujours aussi faiblement équivalentes.

Articles connexes

• Grammaire régulière

• Portail de l’informatique
• Portail des mathématiques