Grammaire hors-contexte

En linguistique et en informatique, une grammaire non contextuelle, grammaire hors-contexte ou grammaire algébrique (type 2 dans la hiérarchie de Chomsky) est une grammaire formelle dans laquelle chaque règle de production (ou simplement production) est de la forme

V → w

où V est un symbole non terminal et w est une chaîne composée de terminaux et/ou de non-terminaux. Le terme « non contextuel » provient du fait qu'un non-terminal V peut toujours être remplacé par w, sans prendre en compte son contexte. Un langage formel est non contextuel (ou hors-contexte) s'il existe une grammaire non contextuelle qui le génère.

Les grammaires non contextuelles sont suffisamment puissantes pour décrire la syntaxe de la plupart des langages de programmation, avec au besoin quelques extensions ; la syntaxe de la majorité des langages de programmation est en fait spécifiée à l'aide de grammaires non contextuelles. Ces grammaires sont cependant suffisamment simples pour permettre la création d'analyseurs syntaxiques efficaces qui, pour une chaîne donnée, déterminent si et comment elle peut être générée à partir de la grammaire. Voir l'analyse Earley pour un exemple d'un tel algorithme. Les analyses LR et les analyses LL sont des méthodes pour analyser des sous-ensembles plus restrictifs de grammaires hors-contexte.

La BNF (Backus Naur form) est la notation la plus communément utilisée pour décrire une grammaire non contextuelle.

Sommaire 1 Exemples 1.1 Exemple 1 1.2 Exemple 2 1.3 Exemple 3 1.4 Autres exemples 2 Dérivations et arbres syntaxiques 3 Formes normales 4 Propriétés des langages non contextuels 5 Voir aussi 5.1 Références

Exemples

Exemple 1

Voilà une grammaire non contextuelle simple :

S → aSb | ε

où | sépare différentes options pour le même non-terminal, et où ε correspond à la chaîne vide. Cette grammaire génère le langage : 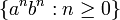qui n'est pas régulier.

Exemple 2

Voilà une grammaire non contextuelle pour les expressions algébriques à trois variables (x, y et z), correctement parenthésées :

S → x | y | z | S + S | S - S | S * S | S/S | (S)

Cette grammaire peut par exemple générer la chaîne « ( x + y ) * x - z * y / ( x + x ) ».

Exemple 3

Cette grammaire décrit le langage consistant en toutes les chaînes contenant seulement des a et des b, et dont le nombre de a est différent du nombre de b :

S → U | V

U → TaU | TaT

V → TbV | TbT

T → aTbT | bTaT | ε

T génère toutes les chaînes ayant le même nombre de a et de b, U génère toutes les chaînes avec plus de a que de b, et V génère toutes les chaînes ayant moins de a que de b.

Autres exemples

Les grammaires non contextuelles ne sont pas limitées aux langages formels en mathématiques. Le linguiste indien Pānini décrivit le sanskrit avec une grammaire non contextuelle.

Dérivations et arbres syntaxiques

Il existe deux manières de décrire comment une chaîne a été générée à partir d'une grammaire donnée. La plus simple est de lister les chaînes consécutives de symboles (en commençant par le symbole de départ et en finissant par la chaîne), appelées proto-phrases, ainsi que les règles appliquées pour passer d'une chaîne à la suivante. Si nous utilisons de plus une stratégie comme « toujours remplacer en premier le non-terminal le plus à gauche », alors, pour les grammaires non contextuelles, la liste des règles appliquées est suffisante. Cela s'appelle la dérivation gauche d'une chaîne. Par exemple, pour la grammaire suivante :

(1) S → S + S

(2) S → 1

la chaîne « 1 + 1 + 1 » a pour dérivation gauche la liste [ (1), (1), (2), (2), (2) ]. De manière analogue, la dérivation droite est la liste des règles lorsque nous remplaçons systématiquement le non-terminal le plus à droite en premier. Dans l'exemple précédent, la dérivation droite est [ (1), (2), (1), (2), (2)].

La distinction entre dérivation gauche et dérivation droite est importante car elle permet dans la plupart des analyseurs syntaxiques de déterminer l'ordre dans lequel les parties d'un programme seront exécutées. Voir par exemple les analyseurs LL et les analyseurs LR.

Une dérivation impose de plus une structure hiérarchique de la chaîne dérivée. La structure de la chaîne « 1 + 1 + 1 », par exemple, est, pour une dérivation gauche :

S→S+S (1)

S→S+S+S (1)

S→1+S+S (2)

S→1+1+S (2)

S→1+1+1 (2)

{ { { 1 }_S + { 1 }_S }_S + { 1 }_S }_S

où { ... }_S indique une sous-chaîne reconnue comme appartenant à S. Cette hiérarchie peut aussi être vue comme un arbre :

           S
          /|\
         / | \
        /  |  \
       S  '+'  S
      /|\      |
     / | \     |
    S '+' S   '1'
    |     |
   '1'   '1'

Cet arbre est appelé arbre de dérivation, arbre d'analyse ou arbre de syntaxe concrète (voir aussi arbre syntaxique abstrait) de la chaîne. Dans ce cas, la dérivation gauche présentée plus haut et la dérivation droite définissent le même arbre syntaxique. Il y a cependant une autre dérivation gauche possible

S→ S + S (1)

S→ 1 + S (2)

S→ 1 + S + S (1)

S→ 1 + 1 + S (2)

S→ 1 + 1 + 1 (2)

qui définit l'arbre syntaxique suivant :

           S 
          /|\
         / | \
        /  |  \
       S  '+'  S
       |      /|\
       |     / | \
      '1'   S '+' S
            |     |
           '1'   '1'

Si pour certaines chaînes du langage d'une grammaire, il y a plus d'un arbre d'analyse, alors la grammaire est dite grammaire ambiguë. Il faut alors faire usage de techniques d'analyse non-déterministe et/ou de techniques adaptées (backtracking, règles de désambiguïsation,...)

Formes normales

Toute grammaire non contextuelle qui ne génère pas la chaîne vide peut être transformée en une forme normale de Chomsky équivalente ou une forme normale de Greibach équivalente. « Équivalente » signifie ici que les deux grammaires génèrent le même langage.

Vu la relative simplicité des règles de production des grammaires en forme normale de Chomsky, cette forme a des implications à la fois théoriques et pratiques. Par exemple, étant donnée une grammaire non contextuelle, on peut utiliser la forme normale de Chomsky pour construire un algorithme qui décide, en temps polynomial, si une chaîne est dans le langage généré par cette grammaire : c'est l'algorithme CYK.

Propriétés des langages non contextuels

• L'union et la concaténation de deux langages non contextuels est un langage non contextuel ; leur intersection ne l'est pas nécessairement.
• L'inverse (image miroir) d'un langage non contextuel est un langage non contextuel ; son complémentaire ne l'est pas nécessairement.
• Tout langage régulier est non contextuel car il peut être décrit par une grammaire régulière.
• L'intersection d'un langage non contextuel et d'un langage régulier est toujours non contextuelle.

Voir aussi

• Grammaire formelle
• Hiérarchie de Chomsky

Références

• (fr) O. Carton, Langages formels, calculabilité et complexité. Vuibert 2008, ISBN 978-2-7117-2077-4
• (fr) J.-M. Autebert et L. Boasson, Transductions rationnelles : Application aux Langages Algébriques. Masson 1988, ISBN 978-2225815041
• (fr) J.-M. Autebert, Langages algébriques. Masson 1987, ISBN 978-2225810879

• Portail de l’informatique