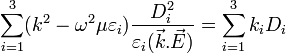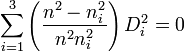- Ellipsoide des indices de refraction
-
Biréfringence
 Le texte apparait en double après avoir traversé le cristal de calcite. C'est la double réfraction, un phénomène caractéristique des milieux biréfringents
Le texte apparait en double après avoir traversé le cristal de calcite. C'est la double réfraction, un phénomène caractéristique des milieux biréfringents
La biréfringence est la propriété physique d'un matériau dans lequel la lumière se propage de façon anisotrope. Dans un milieu biréfringent, l'indice de réfraction n'est pas unique, il dépend des directions de propagation et de polarisation du rayon lumineux.
Un effet spectaculaire de la biréfringence est la double réfraction par laquelle un rayon lumineux pénétrant dans le cristal est divisé en deux. C'est pourquoi, sur la photographie ci-contre, l'inscription apparaît en double après avoir traversé le cristal de calcite. Ce phénomène est caractéristique des milieux biréfringents, à tel point que les termes « double réfraction » et « biréfringence » sont parfois confondus. Le second tire d'ailleurs son étymologie du premier.
Lorsqu'on parle de biréfringence, on sous-entend en général biréfringence linéaire, c'est-à-dire qu'on considère les indices de réfraction pour des ondes polarisées rectilignement. Par analogie, on utilise parfois l'expression biréfringence circulaire pour désigner l'activité optique. En effet, ces deux phénomènes peuvent se décrire de manière très similaire, mais ils ont des origines microscopiques différentes.
Dans le cas particulier des matériaux biréfringents uniaxes, on appelle également biréfringence la valeur de la différence entre les indices de réfraction extraordinaire et ordinaire du matériau (voir la définition de ces termes). La biréfringence peut ainsi être positive ou négative.
Sommaire
Historique
On attribue généralement au danois Rasmus Bartholin la découverte de la biréfringence du spath d'Islande. Ce minéral possède une biréfringence très forte qui permet des observations à l’œil nu, observations que Bartholin décrit dans son ouvrage « Experimenta crystalli Islandici » en 1670. En 1690, le physicien hollandais Christiaan Huygens suppose que pour l'une des images observées à travers le cristal, les rayons suivent un trajet ordinaire. Mais, pour la seconde image, le trajet des rayons n'obéit pas aux lois normales de la réfraction et il propose d'utiliser des ellipsoïdes comme surfaces d'ondes. Il découvre également que la double réfraction disparaît, lorsque les rayons réfractés dans le plan de section principale sont parallèles à la direction de l'axe optique du cristal.
Description des milieux biréfringents
On considère la propagation d'un rayon lumineux polarisé rectilignement dans un milieu biréfringent. De manière générale, la vitesse de cette onde, ou en d'autres termes l'indice de réfraction, dépend de la direction de polarisation du rayon. C'est le propre d'un milieu biréfringent.
Il existe cependant au moins une direction privilégiée pour laquelle l'indice est indépendant de la direction de polarisation. Une telle direction est appelée axe optique du milieu. Dans les milieux naturels, il existe alors deux possibilités correspondant à deux types de milieux :
- les milieux uniaxes qui possèdent un unique axe optique
- les milieux biaxes qui en possèdent deux.
Certains métamatériaux peuvent présenter plus de deux axes optiques. Il n'en sera pas question ici.
Les milieux uniaxes
Les milieux uniaxes ont deux indices de réfraction principaux : on les appelle indices ordinaire et extraordinaire. Ils sont en général notés respectivement no et ne. La différence Δn = ne − no est alors appelée biréfringence (ou biréfringence absolue) du milieu. Pour la plupart des milieux, elle vaut en valeur absolue quelques pourcents.
On distingue deux cas selon le signe de la biréfringence :
- Δn > 0 : le milieu est dit uniaxe positif. L'ellipsoïde des indices a une forme allongée (en forme de cigare).
- Δn < 0 : le milieu est dit uniaxe négatif. L'ellipsoïde des indices a une forme aplatie (en forme de disque).
De très nombreux cristaux naturels sont uniaxes, comme le quartz ou la calcite.
Les cristaux uniaxes appartiennent aux systèmes cristallins trigonal, tétragonal ou hexagonal.
Liste d'indices de réfractions de cristaux uniaxesQuelques indices de matériaux biréfringents
à λ ~ 590 nm (source).Matériau no ne Δn béryl 1.602 1.557 -0.045 calcite CaCO3 1.658 1.486 -0.172 calomel Hg2Cl2 1.973 2.656 +0.683 glace H2O 1.309 1.313 +0.014 niobiate de lithium LiNbO3 2.272 2.187 -0.085 fluorure de magnésium MgF2 1.380 1.385 +0.006 quartz SiO2 1.544 1.553 +0.009 rubis Al2O3 1.770 1.762 -0.008 rutile TiO2 2.616 2.903 +0.287 péridot 1.690 1.654 -0.036 saphir Al2O3 1.768 1.760 -0.008 nitrate de sodium NaNO3 1.587 1.336 -0.251 tourmaline 1.669 1.638 -0.031 zircon (max) ZrSiO4 1.960 2.015 +0.055 zircon (min) ZrSiO4 1.920 1.967 +0.047 Les milieux biaxes
Les milieux biaxes ont trois indices de réfraction principaux notés en général n1, n2 et n3.
Les cristaux biaxes appartiennent aux systèmes cristallins triclinique, monoclinique ou orthorhombique.
Description mathématique, ellipsoïde des indices
L'indice de réfraction d'un milieu est lié à sa permittivité qu'on décrit mathématiquement par un tenseur d'ordre 2. Ce tenseur peut être représenté graphiquement par un ellipsoïde[1] dont les longueurs des demi-axes sont les indices de réfraction principaux. C'est ce qu'on appelle l'ellipsoïde des indices. Cette construction graphique permet de visualiser la relation entre le champ électrique E et le déplacement électrique D ainsi que les directions des axes optiques.
Principe
Soit un milieu optiquement anisotrope. L'indice optique n correspondant à la direction du vecteur unitaire d'excitation électrique
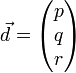 vérifie l'équation
vérifie l'équation 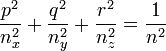 .
.En notant x = n.p, y = n.q, z = n.r, on obtient l'équation de l'ellipsoïde des indices :
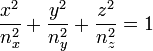
où x,y,z sont bien les coordonnées des points appartenant à un ellipsoïde. Les indices nx, ny et nz sont donnés par les composantes
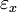 ,
, 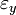 et
et  du tenseur de permittivité électrique du milieu dans ses axes propres, dans l'approximation d'un milieu non magnétique :
du tenseur de permittivité électrique du milieu dans ses axes propres, dans l'approximation d'un milieu non magnétique : 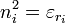 (avec μr = 1 et
(avec μr = 1 et 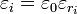 )Démonstration
)DémonstrationIl s'agit de travailler en cartésiennes pour exprimer les équations de Maxwell en fonction du vecteur
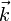 . Une fois démontré que
. Une fois démontré que  , on projette cette équation sur
, on projette cette équation sur 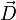 en utilisant
en utilisant 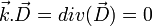 . Les relations entre la vitesse de la lumière, l'indice optique et les permittivités électriques relatives et absolues permettent de conclure.
. Les relations entre la vitesse de la lumière, l'indice optique et les permittivités électriques relatives et absolues permettent de conclure.On effectue les approximations suivantes pour exprimer les équations de maxwell :
- pas de charge extrinsèque : ρex = 0 donc
 (
(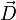 étant le vecteur excitation électrique)
étant le vecteur excitation électrique) - pas de courant extrinsèque :
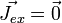 donc
donc 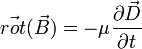 (
(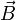 étant le vecteur champ électrique)
étant le vecteur champ électrique) - milieu homogène et linéaire :
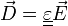
Il s'agit tout d'abord de calculer, en coordonnées cartésiennes, la quantité
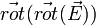 pour une onde plane progressive monochromatique de deux façons différentes. Cette quantité s'écrit
pour une onde plane progressive monochromatique de deux façons différentes. Cette quantité s'écrit 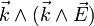 .
.
En utilisant les équations de Maxwell, on peut l'écrire .
.
En utilisant les propriétés vectorielles du produit mixte, on peut l'écrire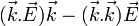 .
.
D'où l'équation de départ du raisonnement :
Plaçons-nous dans le référentiel propre du tenseur
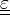 . Il s'assimile alors à une matrice diagonale 3*3. En indiçant par i les coordonnées cartésiennes (x,y,z) du repère, on obtient pour chaque coordonnée l'équation
. Il s'assimile alors à une matrice diagonale 3*3. En indiçant par i les coordonnées cartésiennes (x,y,z) du repère, on obtient pour chaque coordonnée l'équation 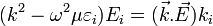 .
.
On divise ensuite l'équation par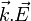 et on la multiplie par Di, sachant que
et on la multiplie par Di, sachant que 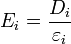 . En sommant les 3 relations obtenues (une pour chaque coordonnée), on a
. En sommant les 3 relations obtenues (une pour chaque coordonnée), on aLe membre de droite correspond au produit scalaire
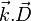 , c'est-à-dire
, c'est-à-dire 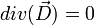 . Puisque le membre de gauche est nul, on peut éliminer le facteur
. Puisque le membre de gauche est nul, on peut éliminer le facteur 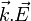 et remplacer
et remplacer 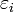 par
par 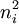 qui lui est proportionnel. De même, en faisant apparaître la vitesse de la lumière dans le vide
qui lui est proportionnel. De même, en faisant apparaître la vitesse de la lumière dans le vide 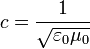 et sachant que
et sachant que 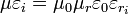 (avec μr = 1 vu que le matériau est considéré non magnétique aux longueurs d'onde considérées), on obtient après avoir tout divisé par n2 :
(avec μr = 1 vu que le matériau est considéré non magnétique aux longueurs d'onde considérées), on obtient après avoir tout divisé par n2 :On peut encore écrire cette égalité
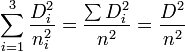 . Introduisant maintenant le vecteur unitaire
. Introduisant maintenant le vecteur unitaire 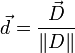 de coordonnées (p,q,r). En divisant l'égalité précédente par D2, on obtient
de coordonnées (p,q,r). En divisant l'égalité précédente par D2, on obtient 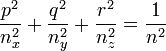 .
.En notant x = n.p, y = n.q, z = n.r, on obtient l'équation de l'ellipsoïde des indices :
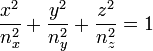
Interprétation physique
Considérons une onde plane électromagnétique. L'analyse vectorielle (en cartésiennes) des équations de Maxwell permet de conclure que les vecteurs suivants sont coplanaires :
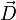 (excitation électrique) et donc le vecteur
(excitation électrique) et donc le vecteur 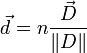 dont les coordonnées interviennent dans l'équation de l'ellipsoïde
dont les coordonnées interviennent dans l'équation de l'ellipsoïde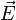 (champ électrique)
(champ électrique)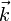 (vecteur d'onde colinéaire à la direction de propagation de l'onde)
(vecteur d'onde colinéaire à la direction de propagation de l'onde)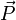 (vecteur de Poynting colinéaire à la direction de propagation de l'énergie)
(vecteur de Poynting colinéaire à la direction de propagation de l'énergie)
Le plan auquel appartiennent ces vecteurs est le plan de polarisation de l'onde. C'est le vecteur
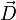 qui est perpendiculaire à
qui est perpendiculaire à 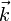 dans les milieux matériels, et non
dans les milieux matériels, et non 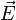 comme c'est habituellement le cas dans le vide.
comme c'est habituellement le cas dans le vide.De plus, on montre que le vecteur
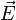 est normal à l'ellipsoïde au point d'intersection avec
est normal à l'ellipsoïde au point d'intersection avec  .Démonstration
.DémonstrationLe vecteur normal à l'ellipsoïde en un de ses points de coordonnées (x,y,z) est
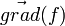 où l'équation de l'ellipsoïde est f(x,y,z) = 0. Le vecteur gradient au point considéré est
où l'équation de l'ellipsoïde est f(x,y,z) = 0. Le vecteur gradient au point considéré est 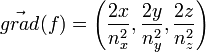 où (x,y,z) sont les coordonnées du vecteur
où (x,y,z) sont les coordonnées du vecteur  . Chacune de ses composantes di (
. Chacune de ses composantes di ( ) est reliée à
) est reliée à 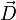 par
par 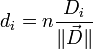 et les composantes de
et les composantes de 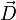 sont reliées à celles de
sont reliées à celles de 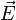 par
par 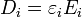 où
où 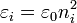 .
.
Le vecteur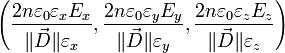 est donc perpendiculaire à la surface au point (x,y,z), et par conséquent, le vecteur
est donc perpendiculaire à la surface au point (x,y,z), et par conséquent, le vecteur  également.
également.Tenant compte de cette condition et de la coplanarité de
 ,
, 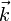 et
et 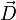 , seules deux orientations sont géométriquement permises pour
, seules deux orientations sont géométriquement permises pour 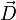 . En effet, l'intersection du plan d'onde (plan perpendiculaire à
. En effet, l'intersection du plan d'onde (plan perpendiculaire à 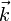 , auquel appartient donc
, auquel appartient donc  ) avec l'ellipsoïde est une ellipse. Les conditions géométriques sont remplies dans 2 cas : lorsque
) avec l'ellipsoïde est une ellipse. Les conditions géométriques sont remplies dans 2 cas : lorsque 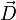 est selon le petit axe et lorsqu'il est selon le grand axe de cette ellipse.
est selon le petit axe et lorsqu'il est selon le grand axe de cette ellipse.- Lorsque
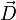 est colinéaire à
est colinéaire à 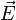 , on parle de rayon "ordinaire". Rien de spécial n'arrive au rayon lumineux
, on parle de rayon "ordinaire". Rien de spécial n'arrive au rayon lumineux - Il existe une autre configuration, qui donne lieu à un rayon extraordinaire. Cette dénomination lui est donnée en raison de la violation des lois de Snell-Descartes par ce rayon. Cette violation n'est pas paradoxale, car les lois de Descartes découlent elles-mêmes des équations de Maxwell dans un cas précis (l'isotropie cristalline), qui, elles, sont toujours vérifiées dans le cas de la biréfringence.
Techniques et outils de mesure de la biréfringence
La mesure de la biréfringence d'un milieu est du ressort de la polarimétrie qui a pour objet plus général la mesure de la polarisation de la lumière. Partant d'un échantillon quelconque qu'on supposera transparent et homogène, une mesure de la biréfringence consiste à déterminer :
- l'orientation des axes propres de l'ellipse des indices,
- la valeur de la biréfringence, c'est-à-dire la différence Δn entre les indices de réfraction valables pour des rayons lumineux polarisés suivant ces deux axes propres.
Entre deux polariseurs croisés
À l'aide d'un compensateur
Biréfringence induite
Il est possible de créer de la biréfringence dans un milieu optiquement isotrope de plusieurs manières.
Par un champ électrique
- on parle d’effet Pockels ou effet électro-optique du premier ordre lorsque la biréfringence est proportionnelle au champ électrique appliqué. Cet effet se produit dans les cristaux non centro-symétriques.
- si la biréfringence est proportionnelle au carré du champ électrique on parle d’effet Kerr. L’effet Kerr peut intervenir pour des gaz et des liquides. Pour les cristaux il est généralement négligeable devant l’effet Pockels qui est beaucoup plus fort, sauf pour les cristaux ferroélectriques proches de la température de Curie tels que la pérovskite.
- l’effet Kerr s’observe également à très haute fréquence : il peut être produit par le champ électrique même du rayon lumineux. On parle alors d’effet Kerr optique, et l’indice de réfraction varie linéairement avec l’intensité lumineuse. C’est cet effet qui est à l’origine du self-focusing (auto-focalisation) des faisceaux lasers de très forte intensité.
Par un champ magnétique
- L’effet Faraday est une biréfringence circulaire ou pouvoir rotatoire qui apparaît si on applique un champ magnétique statique ou de basse fréquence parallèlement à la direction de propagation du rayon lumineux. La biréfringence créée est proportionnelle au champ magnétique. On parle alors de biréfringence magnétique circulaire. Cet effet est utilisé dans les isolateurs de Faraday, ou diodes optiques en télécommunications.
- L’effet Cotton-Mouton (découvert par Kerr (1901) et étudié par Majorana (1902) puis Cotton et Mouton (1904)), appelé parfois effet Voigt exhibe une biréfringence induite par un champ magnétique perpendiculaire à la direction de propagation. La biréfringence est alors proportionnelle au carré du champ appliqué. Il s’agit d’une biréfringence linéaire et non circulaire. L’effet est faible sauf dans des cas particuliers (suspensions colloïdales avec particules métalliques). Il existe également un effet Cotton-Mouton dans le vide (biréfringence magnétique du vide).
- L'effet Kerr magnéto-optique s’observe par réflexion sur une surface d’un matériau soumis à un champ magnétique. Ces effets sont proportionnels au champ magnétique, comme l’effet Faraday, mais ne s’apparentent pas à la biréfringence. Une application bien connue est celle des disques et lecteurs magnéto-optiques.
Par une contrainte mécanique
Les cristaux soumis à des contraintes mécaniques peuvent présenter une biréfringence : on parle de photoélasticité. Lorsque le matériau est transparent, cet effet permet de visualiser les contraintes par interférométrie. Les liquides peuvent également présenter une biréfringence sous contrainte mécanique. Les contraintes étant généralement observées en régime d’écoulement stationnaire, on parle de biréfringence d’écoulement.
Applications
Il existe de nombreuses applications de la biréfringence.
Fabrication d'instruments d'optique
Les propriétés de double réfraction de cristaux tels que le quartz ou la calcite sont utilisées en optique pour former des polariseurs ( prisme de Glan-Thompson, prisme de Glan-Taylor, prisme de Nicol, ...) ou des diviseurs de faisceaux (prisme de Rochon et prisme de Wollaston). On peut aussi utiliser le double indice de réfraction pour fabriquer des lames à retard.
Microscopie en lumière polarisée
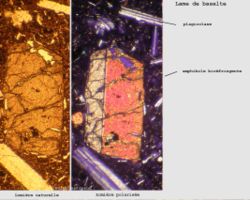
La biréfringence est largement utilisée en microscopie. Le contraste interférentiel de Nomarski et les microscopes polarisants permettent de visualiser des objets de faible contraste : les deux rayons dus à la biréfringence peuvent interférer entre eux. Un des deux rayons, en traversant l'objet à étudier, prend du retard par rapport à l'autre, et l'interférence obtenue dépend de ce retard. Ce microscope permet donc d’observer directement les variations d’épaisseur d’un objet transparent. Cette technique permet de différencier, dans un minéral, différents cristaux de biréfringences différentes, qui apparaîtront avec une couleur et une luminosité différente.
Photoélasticimétrie
La photoélasticité des matériaux permet de visualiser les contraintes présentes à l'intérieur par la méthode de photoélasticimétrie.
Notes et références
- Biréfringence du vide : http://www.phys.ens.fr/IMG/pdf/CRizzo_ENS.pdf - Ellipsoïde des indices, ... : "Optique", Georges BRUHAT - Biréfringences induites, ... : "Polarisation de la lumière", Serge HUARD
Voir aussi
Sites web
- Polarisation et biréfringence
- La double réfraction de la calcite
- Ellipsoïde des indices et test de Tutton
- Portail de la physique
- Portail des minéraux et roches
Catégories : Phénomène optique | Optique non-linéaire | Cristallographie | Minéralogie
Wikimedia Foundation. 2010.