Ellipsométrie

Ellipsométrie: Ellipsomètre dans un laboratoire du LAAS à Toulouse.

L'ellipsomètre calcule uniquement Psi et Delta, et c'est à partir de cela qu'il réalise ses calculs.

L'ellipsométrie est une technique optique de caractérisation et d'analyse de surface, fondée sur le changement d'état de polarisation de la lumière, par réflexion de la lumière sur la surface plane d'un échantillon. Bien que son principe soit connu depuis plus d'un siècle, c'est surtout ces vingt dernières années, avec l'apparition d'ellipsomètres spectroscopiques, que son utilisation s'est généralisée, en particulier dans le domaine de la micro-électronique. L'ellipsométrie est largement mise en œuvre pour la caractérisation des milieux isotropes. On peut citer parmi ses nombreuses applications :

la mesure des constantes optiques des matériaux ;

la mesure de l'épaisseur de couches minces (du nanomètre au micromètre) telles que les couches antireflets, couches d'or, de silice ou de silicium dans les circuits intégrés ;

le suivi in situ de la croissance d'une couche ;

la caractérisation des interfaces liquide-solide ou liquide-liquide ;

l'analyse des couches de protection (électrodéposition, dépôt plasma, polymères), traitement de surface par recuit (application dans la métallurgie) ;

la mesure de rugosité d'une surface ;

la mesure, par scatterométrie, des propriétés (matériaux, géométrie) d'un motif périodique.

Sommaire

1 Principe d'un ellipsomètre spectroscope

2 Réflexion sur des surfaces planes

3 Les angles ellipsométriques

4 Fabricants

5 Références

Principe d'un ellipsomètre spectroscope

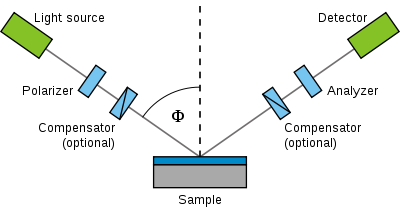
Un faisceau lumineux collimaté est polarisé linéairement grâce à un polariseur. Le faisceau se réfléchit sur l'échantillon, ce qui modifie son état de polarisation. Il passe ensuite dans un analyseur avant d'arriver dans un miroir reconduisant le faisceau dans une fibre optique relié au spectromètre.

Réflexion sur des surfaces planes

Montage schématique d'une expérience d'ellipsométrie.

Considérons une surface et un faisceau incident de lumière polarisée. Une partie du faisceau est transmis ou absorbé à travers la surface, une autre est réfléchie. Dans les deux cas, l'état de polarisation du faisceau a changé. L'ellipsométrie est une technique qui mesure le changement de polarisation dû à la réflexion (ellipsométrie par réflexion) ou à la transmission (ellipsométrie par transmission). Cette modification de l'état de polarisation de la lumière incidente dépend de la surface étudiée.

La propagation du champ électrique suivant Oz peut s'écrire dans un système d'axe cartésien à l'aide du vecteur de Jones, soit $\vec{E} = \left | \begin{array}{cc} E_x = A_x\;\!e^{-i \delta_x}&\\ E_y = A_y\;\!e^{-i \delta_y}&\!\!\!\!. \end{array}\right.$

Les états de polarisation propres d'une onde en réflexion ou en transmission à l'interface de deux milieux isotropes sont les états linéaires, parallèles p et perpendiculaires s au plan d'incidence. Nous introduisons, alors :

les deux composantes orthogonales du vecteur champ électrique incident $\underline{E}^{i}_p$ et $\underline{E}^{i}_s$ (n'importe quel état de polarisation d'une onde incidence peut toujours être décomposé sur cette base).

les composantes du vecteur champ électrique de la lumière réfléchie $\underline{E}^{r}_p$ et $\underline{E}^{r}_s$ ,

les composantes du champ transmis $\underline{E}^{t}_p$ et $\underline{E}^{t}_s$ .

Pour des milieux 1 et 2 homogènes le changement d'indice est brusque à l'interface et si les milieux sont isotropes la loi de Descartes s'applique : $\underline{N}\;\!_1\;\!sin\;\!\theta_1=\underline{N}\;\!_2\;\!sin\;\!\theta_2$ avec $\underline{N} = n-ik$ , indice de réfraction complexe, où $n$ représente la partie réelle de l'indice de réfraction et $k$ l'indice d'absorption.

Les conditions aux limites appliquées aux équations de la théorie de Maxwell, ainsi que l'équation de conservation de l'énergie permettent d'établir les équations de Fresnel : $\underline{r}\;\!_p = \frac{\underline{E}_p^r}{\underline{E}_p^i}=\frac{\underline{N}_2\;\!cos\;\!\theta_1 - \underline{N}_1\;\!cos\;\!\theta_2} {\underline{N}_2\;\!cos\;\!\theta_1 + \underline{N}_1\;\!cos\;\!\theta_2}$ et $\underline{r}\;\!_s = \frac{\underline{E}_s^r}{\underline{E}_s^i}=\frac{\underline{N}_1\;\!cos\;\!\theta_1 - \underline{N}_2\;\!cos\;\!\theta_2}{\underline{N}_2\;\!cos\;\!\theta_2 + \underline{N}_1\;\!cos\;\!\theta_1}$ .

$\underline{r}\;\!_p$ et $\underline{r}\;\!_s$ sont les coefficients de réflexions complexes caractérisant la réflexion. Dans le cas des milieux transparents on détermine un angle d'incidence $θ B$ particulier, l'angle de Brewster, tel que $tan \theta_B = \frac{\underline{N}_1}{\underline{N}_2}.$ A l'angle de Brewster le coefficient $R p$ s'annule. La polarisation du faisceau réflechi est alors rectiligne et perpendiculaire au plan d'indidence.

Les angles ellipsométriques

La modification du champ électrique après réflexion sur l'échantillon peut être représentée par deux coefficients agissant sur chaque composante du champ électrique :

le coefficient de réflexion de l'échantillon pour la polarisation parallèle au plan d'incidence

$\underline{r}_p=\frac{\underline{E}^r_p}{\underline{E}^i_p}=\frac{|\underline{E}^r_p|}{|\underline{E}^i_p|} \;\!e^{i(\varphi^r_p-\varphi^i_p)} = |\underline{r}_p|\;\!e^{i\delta_p}$

le coefficient de réflexion de l'échantillon pour la polarisation perpendiculaire au plan d'incidence

$\underline{r}_s=\frac{\underline{E}^r_s}{\underline{E}^i_s}=\frac{|\underline{E}^r_s|}{|\underline{E}^i_s|} \;\!e^{i(\varphi^r_s-\varphi^i_s)} = |\underline{r}_s|\;\!e^{i\delta_s}.$

Les modules $|\underline{r}_p|$ et $|\underline{r}_s|$ représentent l'atténuation de l'amplitude et leur argument, $δ p$ et $δ s$ , le changement absolu de phase dû à la réflexion.

Le changement de polarisation, qui résulte de la différence de comportement en amplitude et en phase des ondes $p$ et $s$ , peut être caractérisé par la réflectance complexe $\underline{\rho} = \frac{\underline{r}_p}{\underline{r}_s}=\frac{|\underline{E}^r_p|}{|\underline{E}^i_p|}\frac{|\underline{E}^i_s|}{|\underline{E}^r_s|} \;e^{i(\delta_p - \delta_s)}$ que l'on écrit plus couramment $\underline{\rho} = tan\Psi\;\!e^{i\Delta}$ avec $tan\Psi = \left|\frac{\underline{r}_p}{\underline{r}_s}\right|$ représente le rapport des modules et $Δ = δ p - δ s$ la différence des phases.

Les angles $Ψ$ et $Δ$ , caractéristiques de la surface étudiée, sont appelés angles ellipsométriques. Dans un milieu isotrope, ils ne dépendent que de la longueur d'onde $λ$ et de l'angle d'incidence $θ$ et $0 \leq\Psi < \frac{\pi}{2}$ et $0 \leq\Delta\leq2\pi$ .

$|\underline{\rho}|$ est en général différent de l'unité, cela signifie que les deux composantes optiques incidentes sont différemment atténuées et différemment retardées par la réflexion. La connaissance des phases et des amplitudes absolues n'est pas nécessaire et rend la mesure indépendante des fluctuations éventuelles de la source.

Fabricants

Voici les principaux fournisseurs d'éllipsomètres :

HORIBA/Jobin-Yvon

SENTECH Instruments

J.A. Woolam

Références

K.D. Möller, Optics, University Science Book, 1988.

R.M.A. Azzam and N.M. Bashara. Ellipsometry and polarised light. North-Holland, New York, 1977.

http://www.jawoollam.com/tutorial_1.html. Site internet très bien fait pour apprendre le principal sur l'ellipsométrie.

Portail de la physique

Catégorie :
Optique

Contenu soumis à la licence CC-BY-SA. Source : Article Ellipsométrie de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

ellipsométrie — ● ellipsométrie nom féminin Technique permettant de mesurer l état de polarisation de la lumière. (Elle est utilisée pour l étude des couches minces.) … Encyclopédie Universelle
Ellipsometrie — Die Ellipsometrie ist ein Messverfahren der Materialforschung und der Oberflächenphysik, mit dem dielektrische Materialeigenschaften (komplexe Permittivität beziehungsweise Real und Imaginärteil der komplexen Brechzahl) sowie die Schichtdicke… … Deutsch Wikipedia
Ellipsometrie — El|lip|so|me|t|rie [↑ Elliptizität u. ↑ metrie], die; , …tri|en: auf der Messung der Elliptizität reflektierten Lichts beruhende Methode zur Bestimmung von Dicke u. Refraktion dünner Schichten. * * * Ellipsometrie [zu Ellipse und. ..metrie] die … Universal-Lexikon
Ellipsometrie — elipsometrija statusas T sritis Standartizacija ir metrologija apibrėžtis Elipse poliarizuotos šviesos atspindžio tyrimas. atitikmenys: angl. ellipsometry vok. Ellipsometrie, f rus. эллипсометрия, f pranc. ellipsométrie, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
ellipsométrie — elipsometrija statusas T sritis Standartizacija ir metrologija apibrėžtis Elipse poliarizuotos šviesos atspindžio tyrimas. atitikmenys: angl. ellipsometry vok. Ellipsometrie, f rus. эллипсометрия, f pranc. ellipsométrie, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Ellipsometrie — elipsometrija statusas T sritis Standartizacija ir metrologija apibrėžtis Elipse poliarizuotos šviesos poliarizacijos laipsnio matavimas. atitikmenys: angl. ellipsometry vok. Ellipsometrie, f rus. эллипсометрия, f pranc. ellipsométrie, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
ellipsométrie — elipsometrija statusas T sritis Standartizacija ir metrologija apibrėžtis Elipse poliarizuotos šviesos poliarizacijos laipsnio matavimas. atitikmenys: angl. ellipsometry vok. Ellipsometrie, f rus. эллипсометрия, f pranc. ellipsométrie, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Ellipsometrie — elipsometrija statusas T sritis Standartizacija ir metrologija apibrėžtis Optiškai poliarizuoto šviesos pluošto, tam tikru būdu atsispindėjusio nuo paviršiaus, elipsiškumo pokyčio matavimas. atitikmenys: angl. ellipsometry vok. Ellipsometrie, f… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
ellipsométrie — elipsometrija statusas T sritis Standartizacija ir metrologija apibrėžtis Optiškai poliarizuoto šviesos pluošto, tam tikru būdu atsispindėjusio nuo paviršiaus, elipsiškumo pokyčio matavimas. atitikmenys: angl. ellipsometry vok. Ellipsometrie, f… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Ellipsometrie — elipsometrija statusas T sritis fizika atitikmenys: angl. ellipsometry vok. Ellipsometrie, f rus. эллипсометрия, f pranc. ellipsométrie, f … Fizikos terminų žodynas

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts